“同心协力”项目多因素分析研究

胡悦, 朱家明, 凤君仪

“同心协力”项目多因素分析研究

胡悦1, 朱家明2, 凤君仪3

(1. 安徽财经大学 会计学院, 安徽 蚌埠, 233030; 2. 安徽财经大学 大数据学院, 安徽 蚌埠, 233030; 3. 安徽财经大学 管理科学与工程学院, 安徽 蚌埠, 233030)

运用能量守恒、动量定理等物理原理, 借助赫兹函数、脉冲规律以及触觉共享控制模式对“同心鼓”项目策略进行研究, 综合运用了各类绘图软件及MATLAB等编程软件, 对该项目进行多角度受力分析, 构建了基于非合作博弈论的“同心鼓”项目策略研究模型, 得出不同发力时机以及用力大小对该项目结果的影响, 为鼓面倾斜情况制定了调整策略并进行了方案实施效果评估。

同心鼓; 博弈论; 动能守恒定律; MATLAB

“同心鼓”也叫击鼓颠球, 这是一个以团队挑战为主的项目, 挑战团结协作的能力。“同心协力”项目的完成度是团队协作能力的体现, 项目道具是一面双面鼓, 鼓壁中间固定多根绳子, 绳子在鼓壁上的固定点沿圆周呈均匀分布。每根绳子长度相同, 团队成员每人牵拉一根绳子, 维持鼓面的水平。项目开始时, 球从鼓面中心上方竖直落下, 队员合力使球在鼓面上连续颠起, 颠球过程中, 队员只可接触绳子末端, 不可触碰其他部分。该项目需要考虑每个队员的用力方向、时机和力度。精确控制这3大因素, 可使其顺利而持久地进行下去。

石富强[1]在Hertz单性接触和Thornton理想弹塑性接触的接触上, 综合考虑材料的应变率敏感性、应变强化特征等引起屈服后应力应变非线性关系的因素, 提出出新的碰撞接触力模型, 更加准确地揭示了碰撞过程的详细信息。但由于是基于碰撞过程的理论建模, 未进行实证分析, 不能证明模型的可行性。温奇生[2]对一般平面机构运动副的冲量关系、一般平面机构碰撞系统动定性、碰撞分析方法进行了探讨研究, 并结合曲柄摇杆机构受小球碰撞这一实例, 进行分析求解, 最后采用ADAMS进行动力学仿真分析验证。针对目前平面机构碰撞分析方法(如高斯最小约束原理法、基于罚函数连续接触力法)中存在的一些问题, 提出采用基于动量定理和恢复因数法来对一般平面机构进行碰撞分析。这种碰撞分析虽然更加合理, 但要对系统进行多次调整, 增加了碰撞过程选择时间。

总而言之, 现有的文献或多或少都有其不足之处, 相关研究大多基于理论层面, 缺乏经验及数据支持, 需要加以完善。

1 数据来源及模型假设

本文数据来源于2019年全国大学生数学建模竞赛B题, 为了更好地分析并解决同心鼓的受力问题, 提出以下假设:(1)假设排球和鼓面的材料均匀, 且二者碰撞为完全弹性碰撞; (2)假设排球在上升及下降过程中, 空气阻力忽略不计; (3)假设鼓表面是理想的光滑表面, 不存在摩擦力; (4)假设不考虑排球和鼓面自身的弹力; (5)假设排球与鼓面碰撞过程中, 队员对绳子的拉力恒定不变。

2 基于理想状态的团队最佳协作策略研究

2.1 模型的准备与分析

在每个人都可以精确控制用力方向、时机和力度的理想状态下,要讨论团队的最佳协作策略, 并给出该策略下的颠球高度。通过对不同同心鼓颠球视频的观察, 发现每一个团队出力的时刻皆为球向下运动的时刻, 鼓向上弹起, 并且在鼓由最低点到达最高点间的某一点与小球碰撞, 然后双方同向运动。虽然鼓的最佳时机与小球碰撞的点没有直接关系, 但通过运用物理定理分析, 可以得出它们之间的关系。

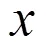
2.2.1 脉冲规律

小球与鼓面的每次碰撞作用完全相同, 因而鼓面对小球的作用力与脉冲有相近的规律。小球与鼓面的每次碰撞作用时间非常短, 可以认为是瞬时完成的, 于是鼓面对小球的作用力用脉冲函数表示为=

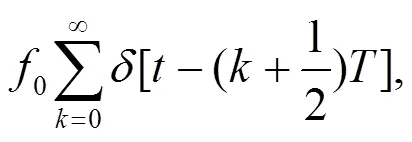
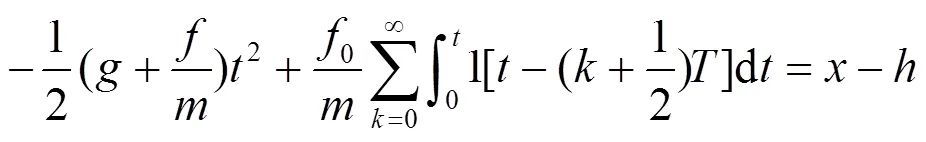
2.2.2 赫兹公式

赫兹公式是提出有关弹性固体接触的理论, 以用于研究2个曲面体之间的接触面及相互作用的关系。此类接触在接触瞬间都是点接触, 但由于材料的弹性变形, 接触点变成了接触面。而本题的排球和同心鼓的接触为弹性接触, 此过程双方皆有不同程度的弹性形变, 故此理论适用于本题求解接触面的压力分布和接触区域的应力分布[3]。

将其中1个曲面体的半径设为无穷大即可假设球体与平面接触, 可用于本题球体与鼓平面的接触应力关系[4]。

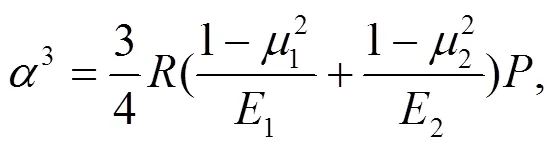
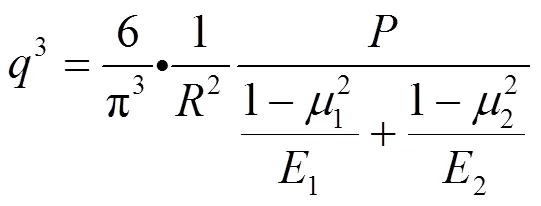
式中:为球体半径;、E为弹性系数;为接触中心压力;为接触圆半径;为曲面体间的距离;为接触中心压力。

结合图1, 由式(3)–(5)可得, 最大接触应力与载荷的立方根成正比。且接触应力与材料的弹性模量及泊桑比有关, 因为接触面积大小与接触物体的弹性变形有关。

2.2.3 动能守恒定理

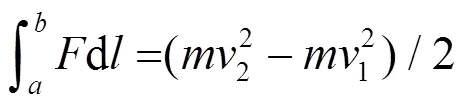
动能定理[5]反映了力对空间的累积效应。

2.2.4 动量定理

动量定理[7]==2-1, 动量定理反映了力对时间的累积效应。

2.3 模型的求解

2.3.1 绳的动态移动对鼓运动产生的能量变化

①绳的静态加载公式=,是绳受的力,是绳的刚度(由绳长决定),是绳子受力过程中位置变量。刚度计算公式K =/,为绳长,是绳模量。由文献[8], 在已知载荷条件下, 绳改变的长度决定, 定义为单位伸长的力=/, = /L=–/cos。同心鼓项目所使用的绳为2 m长引绳, 即PMI拉绳, 据表1可知其模量。

表1 不同种类绳索的静态模量

②绳长的动载荷

绳的伸长可以控制同心鼓运动超过加载距离时停止运动。停止距离越短, 减速度越大。故在绳与鼓的系统中, 计算绳的最大动态力可使用能量守恒定理, 鼓下落时的总能量与绳的应变能相平衡。在鼓下落到最低点时, 鼓的瞬时速度为0, 其下落过程的所有能量都存储在绳的应变能中。

在鼓的重力作用下, 其下落产生的所有能量, 都转化为绳的应变能[8]。由此可得E=E。

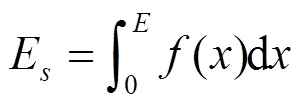
设手作用在绳上的定点0(0,0), 鼓在垂直方向上运动的直线设为++= 0。由图2可得

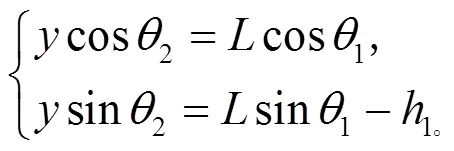
在鼓竖直运动方向的位移变化即势能等于应变能, 又E=, 其中是在竖直方向运动的位移。

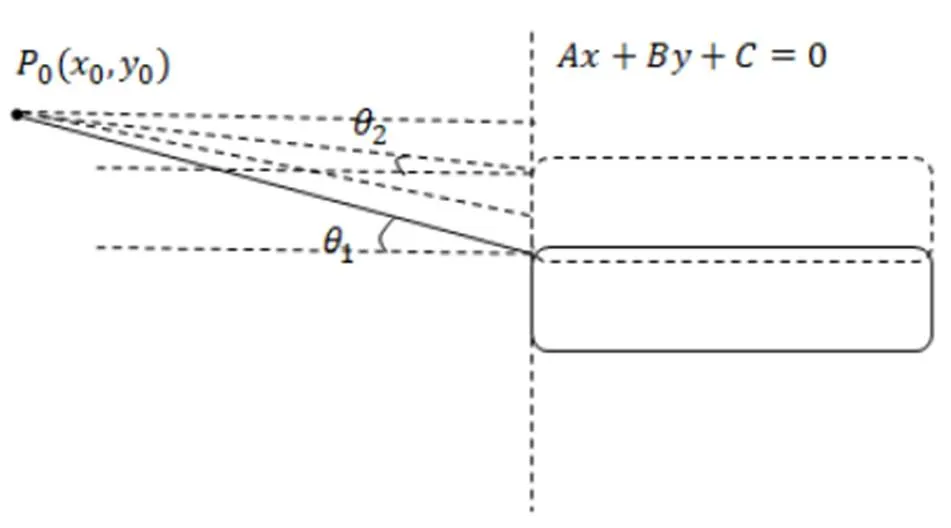
图2 绳位移示意图

在理想条件中, 忽略空气阻力和绳摩擦产生的能量损耗, 得势能公式[10]E=鼓+鼓, = L(1-cos1/cos2)。

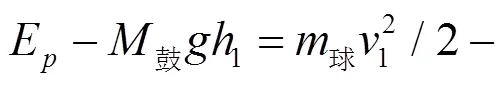
2.3.2 鼓面对小球的撞击力

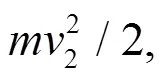
鼓受到绳对其释放的应变能, 产生竖直方向的位移, 此时其动能与势能变化, 鼓面与小球接触时作为1个系统, 以向上为正轴, 向下为负轴, 得其动量公式为:鼓1-球2=鼓3+球4, 其中:1是鼓与球碰撞前的瞬时速度;2是球与鼓碰撞瞬间前的瞬时速度;3是鼓与球碰撞后的瞬时速度;4是球与鼓碰撞后的瞬时速度。

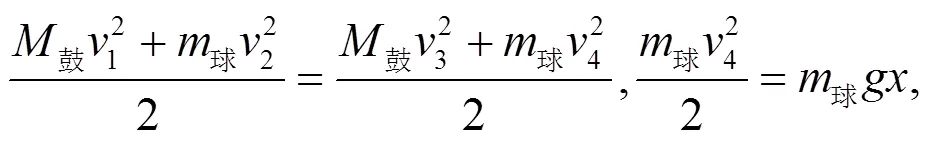
将题给数据代入以上公式, 可得= 40.96 cm。

2.4 模型的优化

原有同心鼓模型只适用于完全理想状态下, 此时每个人都可精确控制用力方向、时机和高度。结合上述结果及实际情况, 对原有同心鼓策略模型进行调整与优化。

优化后的同心鼓模型的最佳策略是使排球在限定时间内, 尽可能多次进行稳定的周期往返运动, 弹起高度不可过高, 并且假设8名队员对绳子的拉力恒定, 以及手持绳子的位置是定点。初始状态, 排球从高处落下时, 双面鼓由水平位置垂直运动至最低点, 将双面鼓的动能和势能转化为绳子的应变能, 双面鼓速度为0时, 绳子与鼓面的倾角最大。随着排球的下降, 队员通过腕部调整, 使传导给绳子的拉力转化为双面鼓向上的弹力, 使双面鼓向上运动, 绳子的应变能再次转化为双面鼓的动能和势能, 使其在上升过程中某一时刻与排球发生碰撞, 碰撞至鼓面时, 排球达到速度最大值。在碰撞的瞬间, 双面鼓的动量一部分维持自身运动, 另一部分转化为排球反向运动的冲量, 给予排球向上运动的初始速度, 使排球先是加速至最大速度再做匀减速运动为0, 达到最高点。在这个过程, 双面鼓先是向上运动至水平状态, 再由于绳子具有弹性, 故双面鼓在达到水平状态时仍会继续向上运动一段高度。

将同心鼓运动按3种情况分类进行分析: a. 用力大小不同; b. 发力时机不同; c. 多因素混合不同。

对情况a进行分析, 当8个队员作用于鼓面的力被分为8部分, 因每个作用点上作用力不同, 导致各点的高度也不相同, 故鼓面发生倾斜。情况b下, 其中有几位队员提前用力, 导致双面鼓受力不均匀, 此时等于双面鼓一边受力, 而另一边不受力, 故鼓面发生倾斜。对情况c进行分析, 结合上述2种情况, 一部分队员提前发力, 另一部分队员施加的作用力较大, 故鼓面发生倾斜。

结合现实情况对理想状态进行分析与改进, 首先是队员对拉力的控制程度, 每1个队员在进行每1次颠球运动时, 无法保证若干次动作是完全一致的, 即力度和手持绳子的位置既会发生轻微变化, 也不能保证每1次运动中所有人都可以同时进行。

综合以上情况, 可设计2个方案的调整策略: d. 8个队员用力一致时; e. 8个队员用力不一致时。

对情况d进行分析, 当排球还未到达鼓面时, 鼓面已保持水平状态, 无需调整; 若鼓面未保持水平状态, 则需对队员对绳的作用力, 队员的位置进行调整。对情况e进行分析, 若8人用力不一致, 则鼓面必然倾斜, 必须进行调整使排球在下落至鼓面时, 鼓面保持水平。

结合技巧和现实情况, 只有在排球落下前保持鼓面水平, 才可达到较为完整的颠球循环过程, 联系题干中提供的数值及项目特征, 调整策略为:

(1) 击鼓。不要靠鼓面击打排球, 只需让球借助鼓面的弹性和排球的弹性自然回弹即可。当发现排球有要停下的趋势时稍微用力, 且此时团队成员应集体用力。

(2) 拉绳。要想保持鼓面平稳, 除队员的自我控制外, 每名队员的两根绳子也应间隔, 不能相邻, 以尽可能保持对鼓面的控制。

(3) 下盘。两脚间距一肩宽, 前后差半步, 用腰腹和臂力控制鼓绳。

(4) 平移。随球移动鼓面时一定要用力拉, 并保证与对应的队友一起平移, 否则鼓面将倾斜。

(5) 拋球。拋球时一定要保证在鼓面上升中让球坠落在鼓面中心点。

(6) 角度。球的下落与垂线的角度不能大于10°。以鼓面40 cm直径计算, 当球的坠落角度出现10°倾斜时, 若球的跳动高度高于60 cm, 则球会落出鼓面。因此不仅要保证球的跳动直上直下, 且球与鼓面的接触点距鼓心20 cm内最佳。

3 基于非合作博弈模型的队员合作与鼓面倾角关系研究

考虑到队员发力时机和力度的不可控造成的鼓面倾斜情况, 并构建模型描述队员发力时机和力度与鼓面倾角的关系。首先, 分组探讨了发力时机与力度两因素对鼓面倾角的影响; 其次选取合适的分析方法, 分别运用物理学的受力分析、动能定理、动量定理, 对各组鼓面倾斜角度进行测度; 最后, 将结果进行对比, 构建模型描述队员发力时机和力度与鼓面倾角间的关系。

3.1 模型的准备与建立——鼓面倾角算法模型

3.1.1 同心鼓受力系统策略——非合作博弈模型

非合作博弈论是指参与者不可能达成具有约束力的协议的博弈模型[12]。由于同心鼓受力控制策略的拉力指令来源于队员对其的控制系统, 如何根据每个人不同的发力情况来控制鼓的倾斜角度成为一个难题。触觉共享控制是一种模式, 当触觉共享控制的控制系统期望获取主导权时, 就会在方向盘上作用一个附加力矩来控制整个车系统。借用此套模式, 将鼓当作车系统, 每个部分的队员通过触觉共享控制, 来进行鼓面位置的控制。为保持鼓面的平衡, 每个部分的队员环环相接, 互相控制互相影响。

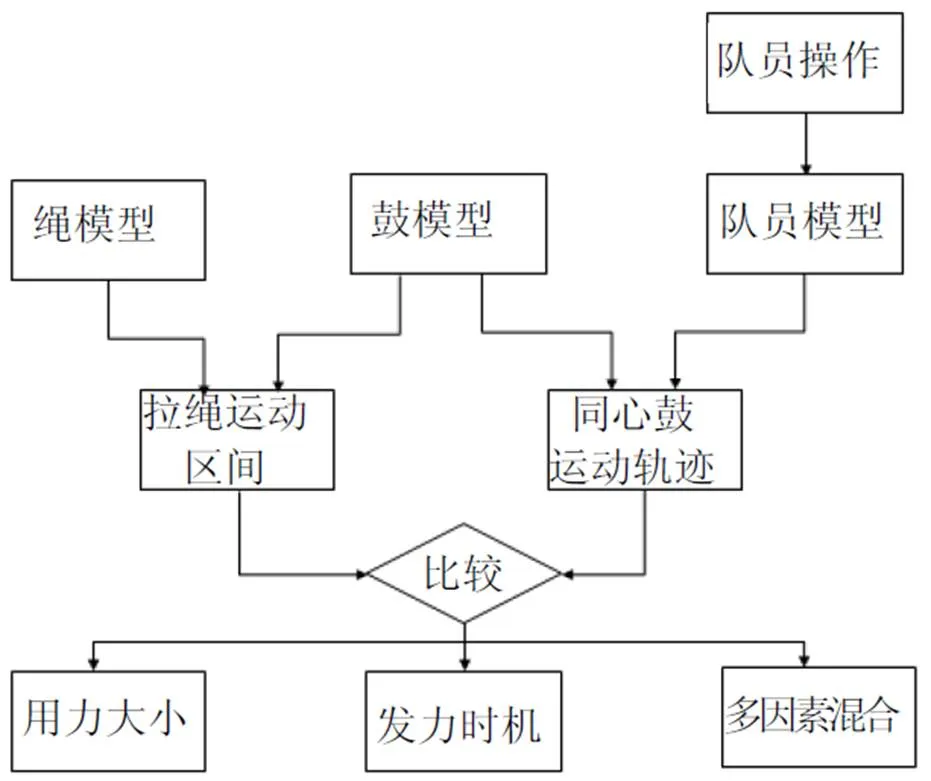
图3 同心鼓控制系统模型流程图

3.1.2 同心鼓控制系统

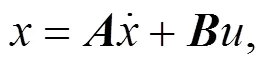
3.2 模型的求解——非合作同心鼓多人控制系统策略

图4 鼓面受力分析侧视图

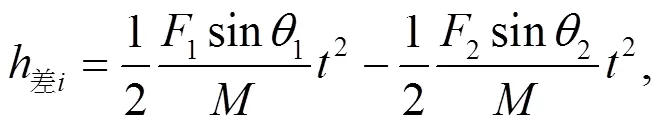
鼓面发生倾斜是由作用力的方向或大小不一致导致的, 此时力的作用点不是鼓的重心, 而是绳子与鼓链接的位置。在其他的情况中, 有部分队员提前发力, 发力时机不同, 所以鼓面各部分的受力不同, 转换为发力大小不同的问题。发力早的点由上升力瞬间作用, 此时鼓面就会倾斜。

4 结论

本文以“同心协力”项目为研究对象, 运用能量守恒、动量定理等物理原理, 借助赫兹函数、脉冲规律对“同心鼓”进行多角度受力分析, 得到理想状态下的团队最佳协作策略, 以及非合作模型下同心鼓多人控制系统的最佳倾角测算。其中, 非合作模型测算出的同心鼓运动参数具有一定的现实意义, 对项目调整策略的优化以及模型的改进推广有所帮助。

[1] 石富强. 两小球弹塑性碰撞过程的动力学分析及建模[D]. 兰州: 兰州大学, 2011.

[2] 温奇生. 一般平面机构的碰撞分析[D]. 福州: 福州大学, 2011.

[3] 毛予廷. 运动与相互作用观念层级模型建构及高中物理教材适应性分析[D]. 重庆: 西南大学, 2018.

[4] 唐安琪. 高中物理机械能守恒相关知识的教学研究[D]. 苏州: 苏州大学, 2016.

[5] 林立兴. 关于《落体法验证机械能守恒定律》实验的几个问题探讨[J]. 湖南中学物理, 2013(2): 35.

[6] 张娜. 一类联图的正规拉普拉斯谱[J]. 湖南文理学院学报(自然科学版), 2018, 30(2): 5–7, 12.

[7] 丁忆梦. 一道力学碰撞问题中动量守恒与角动量守恒辨析[J]. 物理教学探讨,2019, 35(6): 27–29

[8] 刘荣丹, 丁庆红, 张霄燕. 用自由落体运动验证机械能守恒定律实验设计[J]. 实验教学与仪器, 2019, 36(12): 33–34.

[9] 刘国灿, 杨优美. 一类半线性退化抛物方程的全局吸引子[J]. 湖南文理学院学报(自然科学版), 2019, 31(2): 9–12.

[10] 刘银奎. 重视情境创设、培养核心素养——以“动能与动能定理”教学为例[J]. 物理教学探讨, 2019, 37(6): 14–18.

[11] 陈利军. “动能和动能定理”教学设计与反思[J]. 中学物理教学参考, 2016, 45(10): 30–32.

[12] 刘瑞, 朱西产, 刘霖, 等. 基于非合作模型预测控制的人机共驾策略[J]. 同济大学学报(自然科学版), 2019, 47(7): 1 037–1 045.

[13] 杨桂元, 朱家明. 数学建模竞赛优秀论文评析[M]. 合肥: 中国科学技术大学出版社, 2013.

Research on multi-factor analysis of "working together"

Hu Yue1, Zhu Jiaming2, Feng Junyi3

(1. School of Accounting, Anhui University of Finance and Economics, Bengbu 233030, China; 2. Big Data College of Anhui University of Finance and Economics, Bengbu 233030, China; 3. School of Management Science and Engineering, Anhui University of Finance and Economics, Bengbu 233030, China)

Using the physical principles such as energy conservation and momentum theorem, the Hertz function, the pulse law and the tactile shared control mode to study the "Concentric Drum" project strategy, comprehensively using various types of drawing software and MATLAB and other programming software to carry out multiple perspectives on the project Force analysis, constructed a "concentric drum" project strategy research model based on non-cooperative game theory, obtained the impact of different force timing and force on the project results, formulated adjustment strategies and plans for the tilt of the drum surface Implement effectiveness evaluation.

concentric drums; game theory; law of conservation of kinetic energy; MATLAB

O 411.1

A

1672–6146(2020)03–0008–06

10.3969/j.issn.1672–6146.2020.03.002

胡悦, q3535174801@163.com。

2020–02–05

教育部人文社会科学研究项目(19YJCZH069); 安徽省教研项目(2018jyxm1305); 安徽财经大学校教研究项目(acxkjsjy201803zd); 安徽财经大学校教研究项目(acjyyb2018006)。

(责任编校: 张红)