基坑开挖爆破对临近地铁隧道影响研究

李 娟

(重庆市市政设计研究院，重庆 400020)

如今，城市化进程逐渐加快，基础设施的建设也越来越受到重视。在实际工程建设中，在既有的建(构)筑物附近修建新的工程在所难免，比如在既有的隧道附近开挖基坑，需要确保既有隧道工程安全及运营安全，要综合考虑进行基坑开挖设计与施工。

目前，临近既有隧道进行基坑开挖，众多学者进行了大量的研究，也形成了一定的研究成果。比如，吴敏慧等[1]通过实际的现场监测，分析了TRD工法在杭州某临近地铁车站深基坑工程中的应用；张治国等[2]考虑基坑开挖引起的坑底和四周坑壁土体同时卸荷产生的影响，提出了基坑开挖对临近地铁隧道纵向变形影响的两阶段分析方法；肖同刚[3]根据隧道变形监测数据，就基坑开挖对临近地铁隧道的影响进行了分析；周丁恒[4]以某临近地铁车站和区间隧道的深基坑为研究对象，对施工顺序进行优化组合，提出了加强垫层、增设型钢支撑、隔离桩及加固、施工荷载控制等控制措施；许俊超[5]利用有限元分析软件，对临近地铁深基坑的开挖及支护进行了数值模拟，分析了地铁隧道的沉降及变形影响，提出了合理的保护措施。

可以看出，在临近既有隧道基坑的研究方面，主要集中在变形分析方法、施工方法、监测等方面，对于基坑开挖爆破对临近隧道的影响研究鲜有成果出现。本文以重庆某临近既有隧道基坑开挖爆破为实际工程背景，采用数值分析方法，分析爆破荷载对隧道的支护锚杆及衬砌结构的受力特性影响，所得结论可为该工程提供参考，也可为相关的技术人员以及类似工程提供有益借鉴。

1 有限元模型

1.1 工程地质概况

根据地质勘查报告，上覆土层为少量第四系全新统人工填土和残坡积层，下伏岩层主要为侏罗系中统沙溪庙组粉砂岩、泥岩及砂岩，砂岩居多，且该层的分布较为连续稳定。

该工程为临近既有隧道基坑爆破开挖，模型平面见图1。模型平面尺寸大致为65 m×50 m，既有地铁隧道为多心圆结构，直径约为5.1 m，隧道距离基坑底部约为10 m，距离右侧的直线距离为8.5 m。

图1 模型剖面(单位:m)

1.2 计算模型

采用FLAC3D有限元分析软件进行建模，模型尺寸为65 m×50 m×50 m。为简化分析，突出主要问题，将砂岩层作为模型土体建立的主要对象，采用摩尔-库伦本构模型。沿隧道轴向取50 m的长度建立三维有限元模型(图2)。

图2 三维有限元模型

静力计算分析时，在模型左侧、前侧、后侧设置水平约束，底部设置水平和竖向约束，在分析中不考虑排水固结影响；静力部分完成计算动力部分时，将位移场与速度场清零，模型的右侧面与顶面设置为自由边界，其余设置为粘滞(不反射)边界。

为便于计算分析，选取隧道二次衬砌结构轮廓线一些特征点(图3)。

图3 隧道周边特征点示意

根据依托工程的实际开挖情况，本次深基坑爆破开挖对临近既有隧道的动力影响计算过程分以下步骤：

第一步：建立模型并划分网格，平衡初始地应力；

第二步：开挖隧道，并使用内置结构单元加上隧道的衬砌与锚杆；

第三步：开挖基坑的第一级台阶，并平衡地应力；

（1）显著降低水稻各部位稻米中镉和砷的含量且提升稻米产量。（2）有利于酸性镉污染土壤改良和镉/砷在水稻根表的吸附固定，可抑制镉和砷向水稻内部迁移。

第四步：开挖基坑的第二级台阶，并平衡地应力；

第五步：将位移场与速度场清零，并在第二级台阶上下高3 m的位置输入爆破动荷载，观察隧道衬砌与锚杆的动力响应情况。上述各步开挖模型如图4所示。

图4 各步开挖模型示意

1.3 材料参数

混凝土为C30，弹性模量取30 GPa，泊松比取0.2。钢筋混凝土密度取2.5 g/cm3。衬砌及锚杆在模型计算过程中直接选用FLAC3D内部的结构单元进行简化模拟。锚杆各方向间距为1 m，为了方便观测不同深度锚杆的轴力差异，段数取3段。

1.4 动荷载

在FLAC3D动力计算中，动力荷载输入可以采用加速度时程、速度时程、位移时程、应力时程4种方式。若采用粘滞边界条件，则必须输入速度时程进行分析。由于此次没有直接采集爆破台阶炮孔位置的振动数据，取规则的正弦波，频率为25 Hz，速度为35 cm/s，方向沿着X轴负方向，振动总时长为0.3 s。

2 结果分析

采用数值模拟方法，结合开挖要求，主要从锚杆轴力、隧道衬砌结构振动速度、隧道衬砌结构应力等方面进行分析。

2.1 锚杆轴力分析

模拟分析发现，爆破荷载作用下，在极短的时间内，隧道锚杆单元轴力迅速增大，锚杆单元总体轴力分布如图5所示。

图5 锚杆单元轴力分布

取各根锚杆中轴力的峰值绘制在隧道结构线外侧(图6)。分析发现，在爆破荷载作用下，既有隧道锚杆单元的轴力分布有以下规律：

图6 各锚杆轴力峰值(单位：kN)

(1)整体来看，右侧隧道(迎爆)各位置锚杆轴力相对左侧(背爆)较大，说明爆破荷载对迎爆侧的影响要大于背爆侧。

(3)从锚杆单元轴力分布图可以看出，锚杆轴力并非呈现均匀分布，在杆件中部轴力最大，沿着轴向向两端逐渐减小。

2.2 隧道衬砌结构振动速度分析

本次动力部分计算模拟的动荷载加载位置基本位于两条既有隧道的斜上方。在爆破开荷载影响下，两条隧道衬砌的不同节点位置必然会受到影响。

图7、图8给出了不同衬砌特征点编号的振动速度变化曲线。可以看出，受到爆破荷载影响时，各衬砌节点的X方向振动速度变化最为明显，其次为Z方向振动速度，而Y方向振动速度最小，几乎可以忽略不计，且迎爆侧各节点的三向速度峰值也比背爆侧各节点要大，其中迎爆侧各节点X方向振动速度峰值约为10.2 cm/s，而背爆侧各节点X方向振动速度峰值约为8.3 cm/s。

图7 左侧隧道衬砌节点三向振速峰值变化

图8 右侧隧道衬砌节点三向振速峰值变化

2.3 隧道衬砌结构应力分析

既有隧道的衬砌结构，在爆破地震波的作用下会发生复杂的动力响应，衬砌混凝土由于要承受压缩波、拉伸波的反复作用，其内部应力也会随着地震波的作用时而受压、时而受拉。衬砌结构单元的应力大小与其在空间的位置分布有关。

图9给出了右侧隧道各衬砌特征点的压应力变化曲线。在爆破地震波影响下，隧道衬砌结构单元的应力变化因空间位置的不同而出现较大差异，压应力与拉应力峰值的差别也较大。迎爆侧单元的动压应力峰值明显大于其他位置的峰值，其中，最大的为位于迎爆侧拱脚处的15号单元，从动压应力方面来说，在一次爆破过程中，迎爆侧拱脚位置在整个既有隧道衬砌结构中最不利。

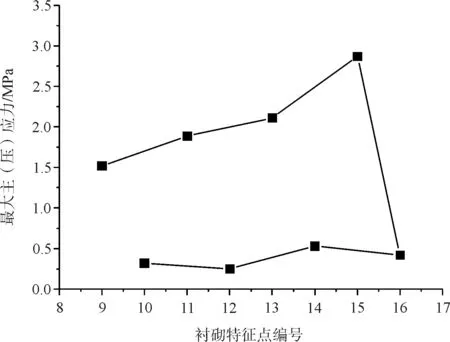
图9 右侧隧道衬砌各点最大压应力峰值

背爆侧与仰拱处的结构单元的动压力峰值均较小，位于仰拱处的单元的动压应力峰值变化很小，基本在0.4～0.5 MPa左右，而隧道中墙位置处的12号单元的动压应力峰值在所有单元中最小，只有0.23 MPa。

在单元的最大主(拉)应力时间历程曲线中，与动压应力峰值相比，动拉应力值峰值要小得多，然而由于混凝土结构的抗压强度要比抗拉强度大很多，所以依然有必要对动拉应力进行分析。图10给出了右侧隧道各节点的拉应力变化曲线，可以看出，15号节点受到拉应力最大，即拱脚处受到影响最大。

图10 右侧隧道衬砌各点最大拉应力峰值

3 结论

以某临近既有隧道基坑爆破开挖为实际工程背景，采用有限元数值计算方法，对爆破荷载作用下隧道锚杆轴力、衬砌结构振动速度及衬砌结构应力进行分析，可以得到以下主要结论：

(1)迎爆侧隧道锚杆所受轴力要大于背爆侧隧道锚杆，表明爆破荷载对迎爆侧隧道锚杆影响较大；锚杆中部轴力最大，向两端逐渐减少。

(2)迎爆侧和背爆侧隧道锚杆的轴力变化规律相似，主要体现为拱顶处轴力最大，拱脚处轴力最小，最大轴力约为6.78 kN。

(3)爆破荷载作用下，不同方向的衬砌节点振动速度差异较大。X方向振动速度变化最为明显，其次为Z方向振动速度，而Y方向振动速度最小。

(4)迎爆侧拱脚位置动压应力和拉应力均最大，表明在整个既有隧道衬砌结构中拱脚位置最不利。