基于进化算法的一维多相声子晶体拓扑优化设计
2020-07-18郭凯红许卫锴
郭凯红,赵 铮,许卫锴
(1.海装装备审价中心,北京 100071;2.南京理工大学能源与动力工程学院,南京 210094;3.沈阳航空航天大学,辽宁省飞行器复合材料结构分析与仿真重点实验室,沈阳 110136)
0 引 言
一维声子晶体也称为超晶格,由于构造简单,易于制作,因此具有十分广泛的应用前景。超晶格一般由两种或更多种弹性介质按一定的顺序周期叠加而成,其中由两相材料组成的一维声子晶体已经取得了阶段性的成果,并发展了几种常用的带隙分析方法,如集中质量法[10-11],传递矩阵法[10,12]和杆纵振解析解方法[13]等。然而,由于一维两相声子晶体带隙频率往往比较高,且相应的带隙宽带不够大,因此,研究人员开始将目标转移到三相或多相结构上来[14-17],并讨论了结构参数和材料参数对其带隙的影响。
研究表明,声子晶体作为一种复合介质,其结构参数和材料参数是影响其带隙特性的主要因素,通过控制和调整周期性单胞内的材料布局及属性,可以设计出所需的具有特殊带隙特性的复合材料,这需要拓扑优化的思想。基于拓扑优化技术,研究人员对一维和二维声子晶体的微观结构进行了设计[18-24]。然而,已有的工作绝大多数都是设计两相复合材料,对一维三相声子晶体的拓扑优化设计研究仍然较少。
本文将利用遗传算法对一维三相声子晶体进行拓扑优化设计。通过引入改进的二进制变量[20]以描述三相材料单胞,并给出了两个拓扑优化算例。计算结果将为一维多相声子晶体的设计及多目标优化提供理论依据。
1 模型与方法
1.1 声子晶体模型
理想的一维声子晶体结构多由无穷多个无限大平板依次排列组成,且在其中的一个方向上具有周期性。但在实际工程中不可能存在无限大的模型。研究表明[21],有限周期的层状结构即能表现出良好的带隙特性。如图1所示,三种不同的材料周期性交替排列,当弹性波仅沿排列方向传播时,将可能出现弹性波的禁带。
1.2 传递矩阵法
考虑图1所示的一维周期性结构,Floquet’s定理[25]和传递矩阵法[12]是常用的有效方法。在实际的优化设计中,实际的材料层数往往大于3。不失一般性,假设具有n层的一维层合材料,当弹性波在其中的任意单层中传播时,其纵波的控制方程为:
(1)
其中j表示单层的序号,Ej和ρj分别为该层材料的弹性模量和密度。于是,该层的传递矩阵可表示为:
(2)
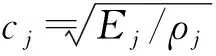
烽火台下,废校场上,四拨人马四向而立。为了体现公道,决斗双方皆避开阳光。风云八虎一方朝南,秦铁崖一方朝北,老太医、乔十二郎等观战之人朝西。乔十二郎出门,照例涂黑额头面颊,一来为掩盖真面目,二来为遮住额头伤疤。乔十二郎一方的队列后有座高高的土墩,那是旧时的检阅台,其上坐着一位重要人物,乃决战见证人,长城大侠魏长安。魏长安须发皆白,然雄风犹在,在北方乃至中原武林威望极高。以上三方都没什么异常,令人狐疑的是,背朝太阳的一方,居然是一队骑兵,乔十二郎数了数,有三十二骑。骑兵身后,停着一顶装饰华贵的马车。
(3)
利用Floquet’s定理,可得到表征周期性层合材料色散关系的特征值问题:
(4)
其中xL表示介质的左边界。求解改特征值问题即可得到表示弹性波带隙的色散曲线(ωvs.k)。
1.3 多相材料的设计变量
一般来说,材料的拓扑优化设计是将设计域离散成细小的网格,然后在网格中填充不同的材料。鉴于遗传算法的二进制变量中仅有1和0两种元素,因此在两相材料的拓扑优化问题中具有独特的优势[26-27],如“1”表示一种材料而“0”表示另一种材料,但在多相材料的设计中将不再适用。另一方面,在一维结构的拓扑优化设计中,不同的染色体还会产生另一种问题:相邻的1和0元素的个数会导致不同层数的拓扑构型,即需要将二进制的设计变量转化为不同材料分层的单胞形式。为了解决这两个问题,引入“二元对”变量
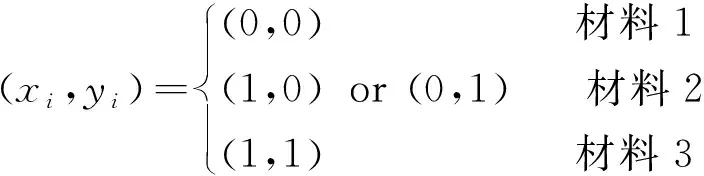
(5)
若将一个设计周期细分为l个细条,则该单胞可由一个长度为2l的染色体表示
a=((x1,y1),(x2,y2),…,(xl,yl))
(6)
定义
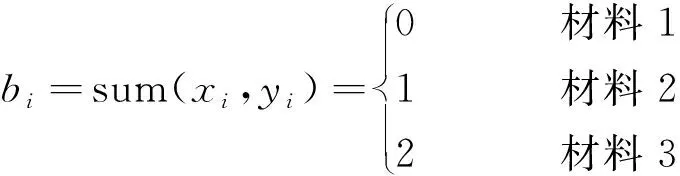
(7)
于是单胞的材料分布可由变量b=(b1,b2,…,bl)表示。进一步的,为了描述单胞内材料的真实分层,参照文献[21],引入逻辑算子:
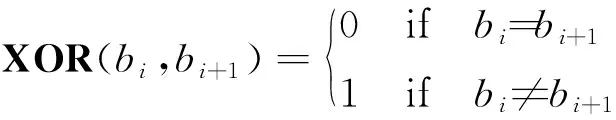
(8)
并定义si=XOR(bi,bi+1),于是s=(s1,s2,…,sl-1)表示材料在单胞中的突变,即si=1时表示即将变成另一种材料。于是,单胞中材料的总层数为
(9)
若引入变量q=(q0,q1,…,qn),其中q0=0,qn=l, 且qj(j=1,2,…,n-1)表示s中元素为1的序号,则单胞中每层材料的厚度和属性分别为
(10)
mj=bqj,j=1,2,…,n
(11)
联立方程(5)~(11)即可将一个任意的染色体a转化为真实的单胞构型,从而计算其带隙性质并利用遗传算法进行优化设计。
2 结果与讨论
本文选取以下三种材料:0为铝,1为橡胶,2为PMMA。材料参数如表1所示。单胞的总厚度为0.18 m。在对单胞进行离散时,尽管更多的分层数可能会产生更好的数值结果,但过薄的分层将导致加工困难和成本增加。因此,为了便于与文献[21]比较,将单胞分为30份,即染色体的长度为60。遗传算法的运行参数见表2。与文献[21]类似,为了保证设计结果的稳定性,每个算例运行5次。

表2 遗传算法的运行参数Table 2 Run-time parameters of GAs

表1 组分材料参数Table 1 Parameters of the component materials
2.1 特定频率下的最大衰减
由式(4)计算的特征值问题通常用虚数表示其禁带,且虚部的大小表示其对弹性波衰减的强弱。因此,特定频率下尽可能大的虚部称为一个重要的目标。该优化问题可表示为
MaximizeF1=ξimag(f*)
(12)
其中ξ=ξreal+iξimag=kd为特定频率f*下的波数。不失一般性,可取f*=20 kHz。
然而,对于一维层合材料的设计容易出现层数越多而衰减越大的情况,但层数的增多意味着制造成本的增加,因此还应考虑材料的总层数对目标函数的影响。为此,本文提出考虑惩罚系数的新目标
(13)
其中,n为单胞内的总层数,a为调节系数,可在-2~30内取值,a越小,则意味着考虑制造成本的权重越大。本文中取a=2。
图2显示了优化结果的单胞构型图和带隙图。如图所示,在考虑了惩罚项的情况下,当单胞内材料层数仅为7层时衰减项即达到了12.87,远大于文献[21]中的结果。
2.2 最大禁带带宽
在设定的频率范围内具有更大的禁带带宽是声子晶体的一个重要设计目标。为此,目标函数可定义为
(14)
其中
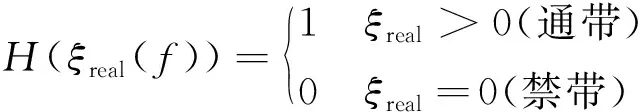
(15)
fmar和fmin分别为频率范围的上下限,在本文中取0和30 kHz。图3显示了优化结果的单胞构型图和带隙图。可以看到,对于一维三相声子晶体来说,即使单胞内材料分层仅为4层,即可得到高达99.21%的禁带,远大于两相材料的情况。另外,带隙的频率也得到了大幅的降低。
3 结 论
本文采用遗传算法,通过引入改进的二进制变量并考虑制造成本的影响,对一维多相声子晶体进行拓扑优化设计。优化算例展现了良好的带隙特征,并得到以下结论:
(1)相比两相材料,三相声子晶体具有更好的带隙特性,在单胞内材料层数较少的情况下即能达到良好的带隙效果;
(2)针对特定频率下的最优隔振目标,设计得到了具有7层材料分层的微结构构型,其衰减项远大于两相材料的结果;
(3)针对特定频率范围内的禁带带宽目标,设计得到了仅有4层材料分层的微结构构型,在获得高达99.21%的禁带带宽的同时,禁带的频率也得到了大幅降低,结果证明本研究提出的方法是可行的。
