融合深度信息的移动机器人跟踪方法研究
2020-07-17潘荣敏王宏伟
潘荣敏,袁 杰,王宏伟,2,米 汤
1.新疆大学 电气工程学院,乌鲁木齐 830047
2.大连理工大学 控制科学与工程学院,辽宁 大连 116024
1 引言
视觉跟踪技术广泛应用在人机交互、自动驾驶、导航制导、无人机、工业机器人等领域,高效的跟踪算法需解决跟踪过程中由环境干扰引起的模型污染问题[1],已成为该研究领域的热点和难点。
在计算机视觉领域,DLT[2]和MDNet方法[3]分别在在OTB50[4]和OTB10[5]中表现出一定准确率,但深度学习模型的复杂性导致其帧率较低,即便是时效性较好的SimFC方法[6]也要依赖高配置GPU,难以满足机器人实时应用。Henriques等提出的核相关滤波器(KCF)算法[7]继承了MOOSE算法[8]的高速率特性,还表现出较高的精度,是众多基于滤波器跟踪算法的模板。作为该类算法的改进,SAMF[9]和DSST[10]方法通过融合多特征并利用尺度池或比例尺改进了目标尺度自适应的不足,LCT方法[11]借用重检测的思想实现了较为稳定的跟踪。但目标及场景动态变化引起的尺度框自适应和目标丢失问题使鲁棒实时跟踪仍然是一个挑战性问题[12]。在众多算法中,特征选取是一个跟踪系统中重要的组成部分,合适的特征可以显著提高跟踪效果[13]。
在移动机器人域领,当行人的腿部特征变化时,采用激光测距仪和相机相结合进行行人跟踪[14-16]的方法容易造成跟踪失败[17]。基于超声波测距的行人跟踪方法[17-18]需要目标体在面向机器人侧携带超声波发射器,应用场景受限。受启发于HOG特征[19]提出的HOD特征[20]和基于RGBD相机的行人检测跟踪策略[21],均证明了利用场景深度信息进行目标跟踪的高效性。
因为其高性能和高效率及易扩展的特性,KCF方法现已是众多优良算法[9-11,22-24]的基准,成为跟踪领域的主流框架。为实现一种实时稳定的机器人视觉跟踪系统,本文在KCF方法的基础上通过融合场景深度信息解决目标尺度框自适应问题及目标被遮挡时的漂移问题,并在移动机器人跟踪应用中具有较好的跟踪效果。
2 核相关滤波器
KCF算法在线更新一个满足岭回归代价函数的相关滤波器θ,大小为W×H的样本X及以其作为生成矩阵的循环矩阵Xw,h为滤波器的训练样本,其中(w,h)∈所有样本是由其对应的图像块通过特征提取函数映射到特征空间下得到的特征矩阵。期望输出y不是二分类的结果,是以跟踪目标所在位置为中心高斯加权后的响应值。

式中φ是通过核相关函数κ映射得到的非线性特征空间,点积 φ(x)⋅φ(x')=κ( )x,x'。正则化系数λ大于0,可避免模型过拟合。
θ的解和循环矩阵X直接相关,由于循环矩阵可由离散傅里叶变换及其生成向量x对角化得到,所以,θ的解可被看作在非线性特征空间下样本的线性组合,表示为:

在对偶空间下,最优化目标系数则由θ变为变量α。α的求解公式为:

式中,F和F-1分别表示离散傅里叶变换和离散傅里叶逆变换,Κxx表示κ(X,X),即样本X的核自相关。常用的高斯核函数为:
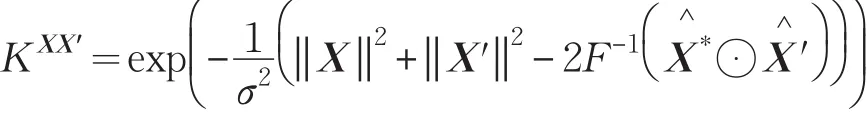
式中,^表示该矩阵的傅里叶变换。
应用中,当获取图像后,以上一帧目标位置为中心,裁剪一块兴趣区域作为目标位置的候选块,并将此候选块的特征矩阵Z输入到前一帧训练的模型,输出 f(Z)的最高响应点位置即为目标区域的中心位置:

其中,ΚXZ表示X和Z的核相关。
模型参数α随着兴趣区域更新,但是很明显的问题是当目标尺寸因距离或者形状的改变而变化时跟踪窗尺度是不变的,对后续目标位置确定产生影响[25],又因缺少跟踪失败检查,在跟踪失败后并没有目标找回机制,在实际应用尤其是机器人应用中存在不足。图1为基于KCF的方法在三维环境跟踪示例中的过程表示,图1的A中小框内书籍为n-1帧的识别结果,目标框尺寸为132×183像素。大框内的兴趣块尺寸为330×458像素,将其划分为82×120个细胞,提取32维HOG特征并图形化表示为图1的B,利用此特征的频域表示进行模型更新。图1的C为n帧输入,方框为根据n-1帧兴趣区域得到的目标位置候选块,提取其HOG特征并进行循环位移扩展样本,其中基础样本的特征表示为图1的D。通过模型匹配得到识别响应结果如图1的E,目标中心位置像素坐标为(252,246),并将结果表示在n帧图像候选块中如图1的F,尺寸为132×183像素,再将n帧识别结果映射到配准好的深度图中得到图1的G,黄色外框为映射得到的初始识别结果。最后通过深度信息对结果进行修正,得到绿色框目标识别结果,尺寸为105×146像素,映射到n帧RGB图像中表示为图1的H。
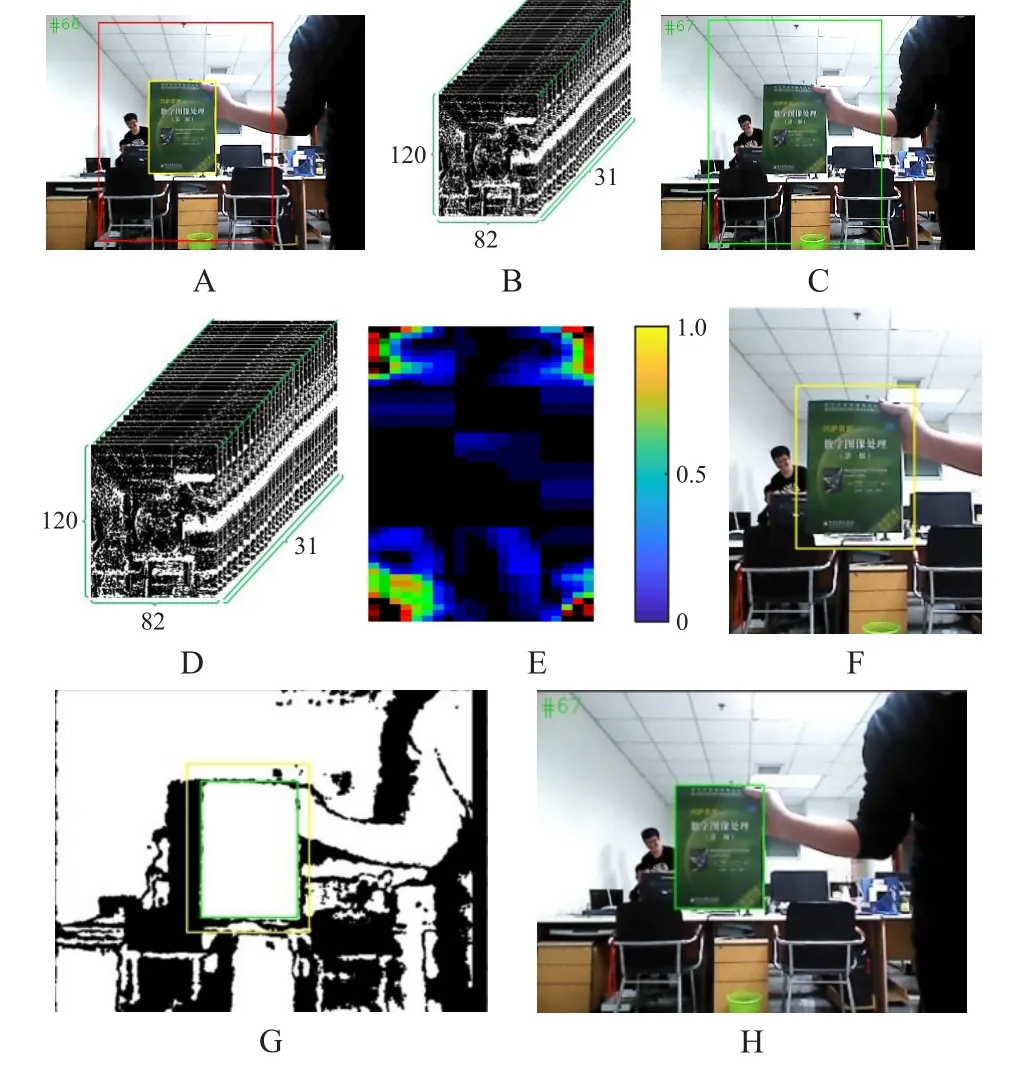
图1 KCF方法在三维场景的应用
3 跟踪系统设计
移动机器人在三维场景中跟踪的系统设计主要在于实时的长时间跟踪方法设计,为让模型更好地适应不同特征空间下的目标特征变化,减少场景腐蚀,目标尺度框自适应、跟踪失败检查以及跟踪丢失后目标找回策略是重要工作。
3.1 目标尺度框估计
深度图可以从背景中反映出目标的轮廓,且目标体本身的深度信息具有高度的自相似性[26],跟踪应用并不要求精准的目标边缘轮廓,只考虑其边缘范围即可,故可以在深度图中通过边缘交叉搜索(Cross-Searching Edge,CSE)的方法进行目标尺度框估计。
在像素坐标系下,任意点( )x,y处的梯度求解公式为:
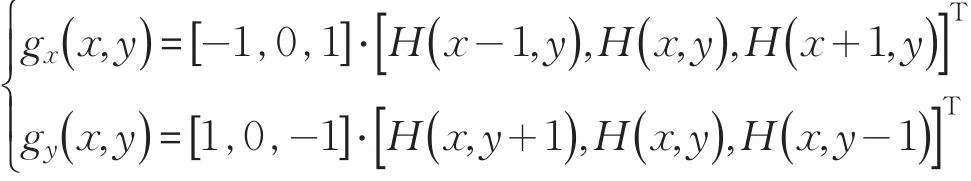
以KCF算法的回归器得到的最大响应点为起始点,沿X负方向计算每点的X方向梯度值,每点的梯度值和边缘阈值比较,超过阈值的点记为(x-m,y),认为其是目标左侧边界点,然后再从起始点沿X正方向计算每点X方向梯度得到目标的右侧边界点(x+n,y)。然后按照式(5)进行目标中点矫正,接着中点开始,分别再沿Y正方向和负方向进行各点Y方向的梯度计算,估计出目标Y方向的尺度边界点。
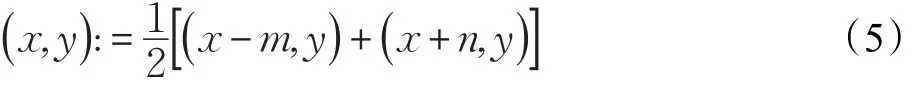
为加快计算速度,在按照上述方法搜索边缘点时可隔点进行梯度计算,这样即对计算结果影响不大又可节省一半的计算时间。如图2为本文方法示意,深色像素点为需要计算梯度的点,其中点A为初始起始点,目标中点矫正后得到点B,箭头所指为梯度取点计算方向,点1、2、3、4分别为该方法依次得到的边界点,最终确定红色的目标框。
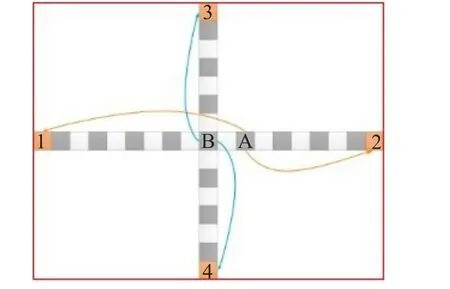
图2 边缘交叉搜索
由于本文方法对目标体轮廓的局部特征敏感,所估计出的目标体尺度可能会偏小,在应用中,会对估计所得目标框的长宽按照一定的系数进行适当放大。此外,由于红外光源为点状衍射导致场景深度图有阴影、系统内外环境不理想,深度图像受高斯噪声、椒盐噪声等干扰,而本文方法对像素质量依赖性强,需进行图像降噪处理。
为平滑图像、消除正态分布噪声,采用二维零均值离散高斯函数对图像进行平滑滤波处理,二维高斯函数为:

式中,G(x ,y)为二维高斯函数点(x ,y )处的值,σ1、σ2为X和Y方向的方差。图像滤波的过程是高斯核和图像做卷积的过程。高斯核是一个长宽均为正奇数的矩形模板,在此应用中取其为一个方形模板,X和Y的方差相等,均为σ,则该高斯核中每个元素的计算公式为:

其中,Ki,j为( )i,j位置的元素值,高斯核元素位置的确定是以中心处元素位置为原点、i轴水平向右为正方向、j轴水平向上为正方向的坐标系,2t-1为方形高斯核的宽度。为适应目标图像各像素点的数据类型,提高滤波效率,现将得到的高斯核元素整数化,整数化过程为:首先将首项归一化,即各元素乘以模板系数和的倒数;然后对各项进行取整;最后在得到的模板前加各整数元素和的倒数即为整数类型高斯核。
图像中的椒盐噪声通常由脉冲响应引起,在深度图中一般表现为数字化极大或极小值,即纯黑或纯白,对应场景含义为极近或极远。而深度相机的有效使用距离为0.6~8 m,故对图像中异点附近的所有点进行剔除,即可避免椒盐噪声的影响。降噪效果如图3所示,图(a)为降噪前深度图,存在许多椒盐噪点和高斯噪点,图(b)为降噪后深度图,减少了噪点影响,平滑了图像。

图3 降噪处理
为进一步降低噪点对边缘检测的影响,增加梯度值的可信度,可将目标点及临近点的梯度和作为判断目标点梯度大小的数值依据,即在计算X方向梯度时,将目标点(x,y)及其左右邻点的梯度和作为(x,y)处的梯度依据,这即是Prewitt算子。为体现目标点的重要性,将目标点梯度权重加大,即为Sobel算子:

其中,Sx、Sy分别为X方向和Y方向的Sobel算子,I为图像点z5附近的图像块,则在Sobel算子下z5处的梯度可为:

如图4所示,上方3张为场景的RGB信息图像,下方3张为对应的场景深度信息图像,图4(a)为场景原图,图4(b)、(c)分别为对应的X方向梯度图和Y方向梯度图,很直观地可以看出在深度图下搜索物体边界要比RGB图下更简单。将图4中行人认为目标点,图4(a)中蓝色点位置为目标中心位置,在深度图中以目标中心点的X方向边界搜索为例,得到图5(a)该点处X方向像素值分布,图5(b)为图5(a)各点对应的X方向梯度值,可以看出在物体边界处存在梯度峰值。应用中,并不需要将Sobel算子与图像做卷积运算,只需以目标响应点为起点按照CSE方法进行边界点检测,减少了计算量。目标框估计效果如图6所示,黄色框为初始目标框,在深度图6的A中利用本方法估计得到绿色框所示目标框,并将其映射到RGB图像中得到图6的B。本文方法不依赖目标体HOG、纹理、形状等特征,故理论上对刚体和非刚体在颜色、光线、几何特征变化时的尺度自适应都是有效的。

图4 梯度图像
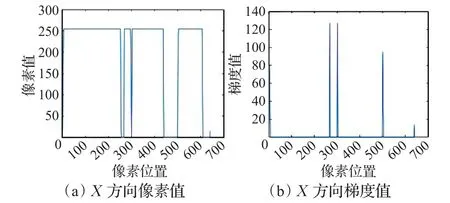
图5 目标中心点X方向像素及梯度

图6 目标尺度框估计
3.2 跟踪失败检查
由于相关滤波器本身就是模板类的方法,不管对样本采用何种特征提取方法,只要在该特征空间下的样本表示发生较大的改变都会对跟踪效果造成严重影响,比如,相关滤波器类方法对采用HOG特征模型下的目标要求不能有快速变形、采用CN颜色特征模型下的目标不能有强烈的光线和颜色变化。在3D环境中短时间内物体深度信息的变化不会特别剧烈,而当目标被遮挡时,遮挡位置处的深度信息会发生突变,因此提出通过轴向相对动能波动(Fluctuations in Axial Relative Kinetic Energy,FARKE)进行跟踪失败检查,FARKE定义式如下:

其中,fe表示轴向相对动能波动的值,D表示物体到相机的相对距离,n+1为当前相关滤波器响应出的目标中心位置,n为前一帧图像中目标中心位置。tn代表n-1到n之间目标丢失的图像帧数,若跟踪正常时tn为1。当目标被遮挡时,fe值会发生明显波动,设定阈值ξ,当fe>ξ时认为目标丢失或被遮挡,ξ与目标体的纵向尺寸及移动机器人相对目标体的速度有关。如果令图像相邻两帧间的更新时间为1,则式(9)涵义为相邻帧间目标在轴向方向相对相机的动能比。因为考虑到了目标早先的深度,相比于仅检测目标位置深度变化量的方法[27]采用动能比的方法更适合快速运动的目标。
fe响应值超出阈值时,为保护模型不被当前帧的遮挡物或环境中其他干扰污染,模型停止更新。
3.3 历史模板池
将通过FARKE检查的图像对应的目标模型保存到历史模板池,在目标跟踪模型被污染后,利用目标面积变化率估计的方法估计目标位移,然后计算取样间隔并从历史模板池抽取模板作为新的目标跟踪模型。目标面积变化率估计方法是一种基于目标框像素数的方法,假设模板池中各模板对应的目标模型准确,且目标体在相邻帧间的位移和形变是连续的即目标被遮挡的过程至少反应在连续的两帧图像中。

式中,ra是目标面积变换率估计值,Sn为第n帧中目标框的面积,a为取样帧数,可参照相机拍照帧率取值,为第n帧目标框的左边缘像素点的X轴坐标,代表右边缘像素点X轴坐标,t代表最终取样间隔帧数,Smax=max{ }Sn-a,Sn-a+1,…,Sn-1,Sn为取样内目标面积的最大值。在目标被遮挡或其他环境干扰引起目标漂移时,FARKE识别出目标丢失,丢弃当前帧对应的跟踪模型,历史模板池作为待取模型库,根据目标面积变化率方法计算所得间隔t,从中选取第n-t帧对应的模型来更新第n+1帧模型参数。
3.4 搜索策略
当目标被大面积物体遮挡再出现后,由于位移发生较大变化,在当前搜索区域可能不会检测到目标,因此根据目标被遮挡时间在一定范围内扩大搜索区域可确保目标跟踪的准确性。搜索策略为:

式中,pad是搜索区域相对目标框尺寸的倍率,初始值为1.5;α是调控系数,本文取0.8。当丢失目标找回后,pad恢复初始值。
如图7所示为应用相对动能波动进行目标跟踪失败检查的过程,上面为遮挡过程中的RGB图像,下面为对应的深度图,目标跟踪结果用绿色框标识。第一组的第657帧图像,目标尺寸面积63×241,距离2.86 m,第二组为目标被遮挡前一帧的第658帧图像,目标尺寸31×192,距离2.96 m,之后目标被遮挡,遮挡物距离为1.73 m,如第三组图所示。设置阈值ξ=16.5,计算出fe=151.29大于阈值,目标丢失,停止模型更新。在目标丢失过程中,令取样帧数a=3,得Smax=15 183,取样间隔t=5,即取目标丢失时的前第5帧模型更新跟踪器。随着丢失帧数增加不断扩大搜索区域,在第四组图即第676帧目标重新出现时,目标已丢失17帧,搜索区域扩大到丢失前目标框区域的20倍范围,跟踪器检测到目标,目标距离3.12 m,计算 fe=2.56小于阈值,通过跟踪失败检查,目标被重新跟踪。

图7 跟踪失败检查
3.5 跟踪系统流程
综上所述,由识别算法或人工框选初始化跟踪目标后,本文跟踪机器人系统的流程如图8所示,图中绿色箭头线代表KCF方法处理进程,其余橘黄色为本文方法实现。
4 实验
为验证所提方法的有效性,在对RGBD相机进行标定和配准后首先完成场景数据采集,然后在数据集上进行规则和不规则几何特征物体形变下的跟踪以及目标体在运动和不运动时被遮挡条件下的跟踪;之后,完成了移动机器人行人跟踪实验。
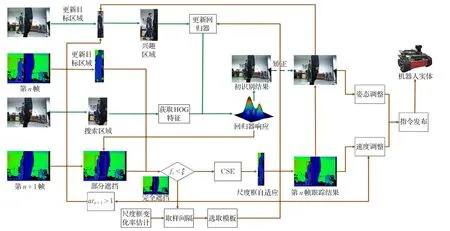
图8 跟踪机器人系统流程
4.1 尺度框自适应
在图9图像序列中,目标体为绿色书籍,由于相对相机轴向方向运动故其在图像不同帧中尺度差异较大。实验表明,KCF方法不能准确适应由距离变化引起的目标尺度变化,而本文方法则有效地解决了这类问题,识别结果能够很好地适应目标尺度的变化,避免了跟踪窗口包含过多环境噪声,有效调整了目标搜索区域。

图9 距离自适应
在图10图像序列中,目标体为黄色书籍,由于旋转其在图像中的几何特征发生变化。KCF方法识别结果不能很好适应目标体变化的几何特征,本文方法的识别结果在这种变化中具有稳定的适应性,能随目标变化自适应尺度框大小和位置。在图序后两帧图中,目标体局部被白色障碍物遮挡干扰,本文方法仍表现出鲁棒的跟踪效果。
为进一步说明,在图11图像序列中,不规则外形的红色玩偶为目标体,其在不同距离和姿态下具有差别较大的外观特征。KCF识别效果没有准确地适应目标体的变化,甚至在一段时间后目标识别框漂移到了大部分图像空间,失去了跟踪结果的有效性,本文方法则表现出较强的可靠性,面对这种变化能够准确稳定地做出目标框调整。
4.2 目标遮挡
在图12图像序列中,在静止目标黑衣少年被路人完全遮挡并短暂消失的情况下,KCF算法受到路人干扰,模型更新错误,目标漂移到路人上面,跟踪失败,本文方法能够在被遮挡时停止模型更新,在遮挡物离开目标又出现后,仍能继续搜索到目标体,继续跟踪。
在图13所示视频序列中,目标体远处少年在运动中被近处静止的黑衣路人遮挡并消失。KCF方法不能适应目标遮挡的情况,本文方法能够在移动目标被遮挡再出现后仍可继续准确检测到目标位置,完成长间跟踪。

图10 形变自适应

图11 不规则目标运动自适应

图12 静止目标被遮挡

图13 运动目标被遮挡
4.3 目标跟踪系统在移动机器人上的应用
4.3.1 机器人系统简介
图14为本文实验采用的移动机器人平台,搭载处理器为Core i5-3230M,主频2.6 GHz,内存8.0 GB的计算机,依赖Ubuntu14.4下的Indigo版本机器人操作系统(ROS),相机采用奥比中光Astra Pro。本文跟踪算法处理速度能够保持在30 FPS以上。图15(a)为Gazebo仿真实验环境界面,图15(b)为真实实验环境。

图14 移动机器人

图15 机器人跟踪实验
4.3.2 实验效果
IR镜头与物体需保持至少0.6 m的距离获取的信息才可靠,并且实际应用中近距离条件下获取的图像中不能完整包括目标体完整特征,且目标在相机径向方向运动时由于相对角速度过大容易引起机器人姿态调整不及时从而丢失目标。为保证在使用过程中稳定可靠,仿真实验和实物验证实验都使跟踪机器人和目标体保持最少1.5 m的距离,因此在曲线运动时二者转弯半径不同,两者轨迹重合度降低,但移动机器人的运动轨迹重合度并不等价于跟踪方法的精度和鲁棒性。图16为传统KCF方法跟踪轨迹,在跟踪过程中即使目标简单运动也很快发生目标漂移,跟踪失败,效果不稳定。图17(a)和(b)分别为本文方法在仿真和真实环境下的跟踪轨迹,移动机器人能够长时间保持对目标的有效跟踪。为进一步验证本方法在机器人跟踪应用的稳定性,分别在无行人遮挡和有行人遮挡以及目标体直线运动和做转弯动作条件下对本文方法和KCF方法进行实验统计,实验结果如表1。从整体效果来看,本文跟踪方法表现稳定,机器人能够保持实时准确的动作响应,说明本跟踪方法对运动目标体具有可靠的跟踪能力。
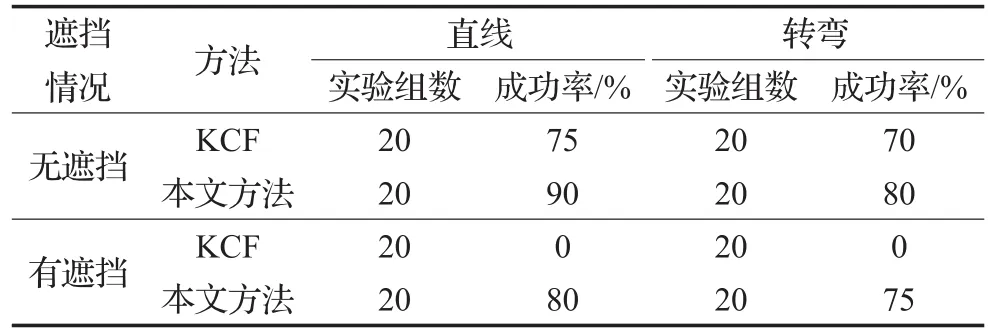
表1 机器人跟踪实验结果
5 结论

图16 KCF方法跟踪轨迹图

图17 本文方法在仿真和真实环境下的跟踪轨迹图
本文基于核相关滤波器提出了融合场景深度信息的机器人跟踪系统。为解决目标框自适应问题,实现了融合场景深度信息的边缘交叉搜索(CSE)方法,在保证实时性的同时避免了跟踪窗口包含过多的环境信息。针对目标在复杂环境下容易被遮挡发生目标漂移的现象,提出了基于场景深度信息的轴向相对动能波动(FARKE)跟踪失败检测方法,能够快速检测出目标是否被遮挡或发生目标漂移;同时根据目标尺度变化构建了含有历史模板池的模型自更新策略,为适当扩大搜索范围建立了目标丢失恢复机制,提高了复杂环境下跟踪的鲁棒性。实验结果证明,本文方法可以有效可靠地应用在3D场景及移动机器人目标跟踪中。
