基于社交和地理信息的兴趣点推荐
2020-07-17郭晨睿
郭晨睿,李 平,2
1.长沙理工大学 计算机与通信工程学院,长沙 410114
2.智能交通大数据处理湖南省重点实验室,长沙 410114
1 概述
随着移动智能设备等技术的快速发展,基于位置的社交网络[1-7](Location Based Social Networks,LBSNs)应运而生,如Foursquare、Gowall和微信等。LBSNs连接了现实世界和虚拟世界,用户通过线下访问现实生活中他们感兴趣的地理位置,并在线上以签到的方式发表评论等信息,与其他用户分享自己在该兴趣点(Points-of-Interests,POIs)的签到体验。LBSNs不仅受到了广大用户喜爱,而且受到学术界和工业界的广泛关注。LBSNs的广泛应用推动了兴趣点推荐系统的发展。在兴趣点推荐系统中融合多种影响因素可以有效提高兴趣点推荐系统的质量。因此,融合多种影响因素构建兴趣点推荐系统是广大学者的主要研究方向。
传统的基于用户的协同过滤算法将两个用户之间的相互影响当作对称的影响,即对于LBSNs中任意的两个用户,彼此的影响是相同的。然而,在现实生活中这种情况并不一定如此,例如:专家可能会对新用户产生影响,但是新用户根本不会影响专家。此外,兴趣点是现实生活中真实存在的地点,用户在兴趣点的签到行为必然会受到用户与兴趣点之间地理位置的影响,即地理影响。文献[4,7]中计算同一用户在一天内签到的两个相邻兴趣点之间的距离,并汇总所有用户签到的结果,获得如图1所示的距离函数。其中,概率值越大表明用户更愿意在该距离处的兴趣点签到。由图1可以看出,随着两个兴趣点之间距离的增加,用户愿意签到访问的概率随之减少。
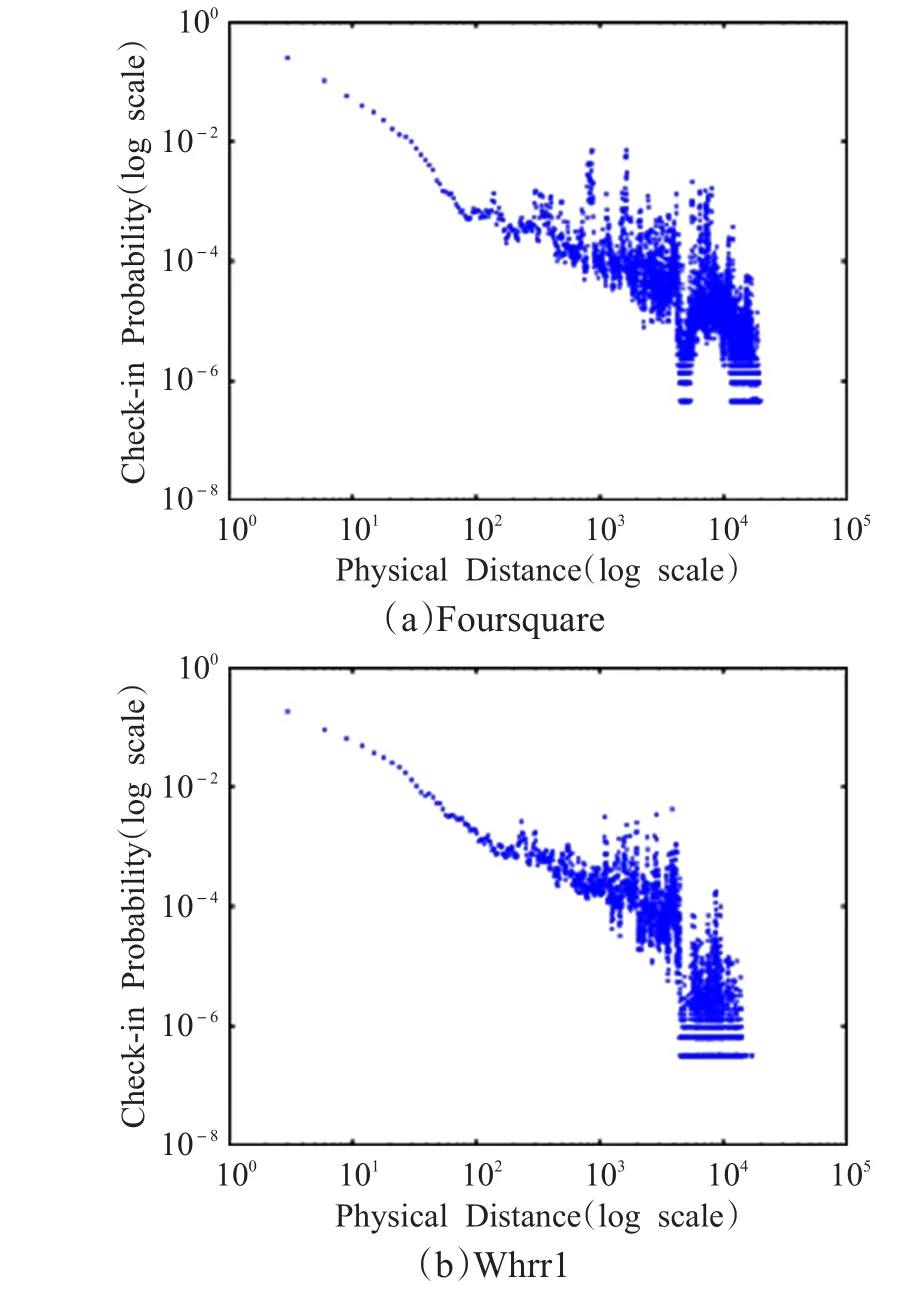
图1 地理影响签到概率分布本文
针对上述问题,本文提出了一种融合用户、社交和地理信息(Fuse Users、Social and Geographic,FUSG)的兴趣点推荐模型。首先,使用一种改进的基于用户的协同过滤算法:非对称用户影响模型计算两个用户间的定向影响,并通过PageRank算法生成用户的全局影响因子来改进非对称用户影响模型;其次,提出了一种融合社交用户之间的居住距离和他们的共同好友的方法来计算用户相似度;然后,利用地理信息挖掘用户的签到特征,生成地理模型;最后,将改进的用户影响、社交影响和地理影响融合成FUSG兴趣点推荐模型。
本文的主要贡献点由以下三个方面:(1)采用非对称用户影响模型和PageRank算法生成用户的全局影响因子来改进基于用户的协同过滤算法进行兴趣点推荐;(2)提出了一种新的计算用户相似度的方法:通过社交用户的居住距离与用户的朋友集合计算用户之间的相似度;(3)融合用户偏好、社交信息和地理信息三种影响因素生成的FUSG模型在真实数据上的精确率和召回率都有所提高。
2 相关工作
主要展示一些与本文相关的最新研究工作,这些工作主要围绕地理影响和社交关系进行兴趣点推荐。
地理影响[4-12],地理影响是区分兴趣点推荐与传统项目推荐的重要因素,用户在兴趣点的签到行为取决于用户和兴趣点的地理特征。文献[4]中Cheng等人提出了一种多中心的高斯模型(Multi-center Gaussian Model,MGM)来挖掘用户的签到历史的多个中心的位置,从而使用地理影响来增强兴趣点推荐的质量,但是由于用户签到数据的稀疏性,难以确定用户签到中心,且很难使用相同的分布对不同的用户进行建模;文献[7]中Zhang等人使用核密度估计将地理影响模型转化为用户的个性化距离分布,实验结果表明,该方法优于MGM,但是在很多真实推荐场景中并不适用,计算复杂度相对较高,且距离分布估计难度较高;因此本文模型采用文献[11]中Ye等人提出的幂函数分布,从距离上拟合用户的空间分布,假设用户签到的地点之间的距离符合幂函数分布。
社交影响[11,13-17],基于LBSNs中的朋友比非朋友会拥有更多的共同兴趣的假设来提高兴趣点推荐的质量。文献[11,14]中Ye等人提出了一种基于朋友的协同过滤(Friend-based Collaborative Filtering,FCF),该方法融合了用户的朋友集合及用户签到的兴趣点集合,但是未考虑用户现实生活中居住距离对兴趣点推荐的影响;文献[15]中在计算社交用户相似度时仅仅考虑了用户的朋友集合,未考虑到用户之间居住距离对用户相似度的影响;文献[17]中Zhang等人提出了基于用户现实生活居住距离的方法计算用户相似度,但是未考虑用户社交关系对兴趣点推荐的影响。因此,本文模型为充分考虑了用户现实居住距离及用户朋友集合对兴趣点签到的影响,提出了一种新的基于社交关系的相似度计算方法。
3 FUSG模型
3.1 非对称用户影响
R=[cul]m×n表示用户u在兴趣点l的签到矩阵,其中m表示用户的数量,n表示兴趣点的数量,矩阵中第i行和第 j列的cul表示用户u在兴趣点l的签到次数。签到次数越多,表明用户u越喜欢趣点l,若用户u未在兴趣点l签到过,则cul=0。
首先,需要计算用户u对其所有签到过的趣点l的平均签到次数 cˉu,如公式(1)所示:

其中,nu表示用户u签到过的兴趣点的总数目。使用用户的平均签到次数cˉu来构建布尔矩阵其中由公式(2)计算获得:

根据矩阵R′构建非对称用户影响矩阵W=[wuv]m×m,其中wuv表示用户u对用户v的影响因子,wuv的计算方式如公式(3)所示:

不同于传统的基于用户的协同过滤算法中使用的对称用户关系矩阵,该用户关系矩阵是不对称矩阵。
假设:(1)用户可以影响的用户越多,则该用户在兴趣点推荐系统中用户全局重要性越高;(2)如果有多个用户可以对目标用户产生影响,则目标用户更容易受到全局重要性较高用户的影响[18]。
基于上述假设,可以得出结论:除了非对称用户影响矩阵之外,全局用户重要性值在提高推荐的准确性方面也起着关键作用。因此,本文使用PageRank算法计算用户的重要性值。直观地说,如果一个用户可以影响的用户越多,该用户的全局影响值越高。目标用户的in-degree表示能够影响他的用户数量,out-degree表示目标用户能够影响的其他用户数量。如果用户u和用户v之间的影响值wuv大于等于平均影响值wˉ,则影响因子等于1,表示用户u可以对用户v产生影响;否则的值为0,用户u不会对用户v产生影响。平均影响值wˉ和影响因子分别由公式(4)、(5)计算得到:


其中,δ(x)是指示函数,当x≻0时δ(x)=1,否则δ(x)=0。
用户u可以影响的用户数目du通过公式(6)计算得到:

随机初始化用户的PageRank值,并使用下面的迭代模型得到用户最终的PageRank值。在每次迭代t中,PageRank的值由公式(7)计算:

其中,Ι∈Rm×1是全1向量,α∈[0,1]是阻尼系数,表示其他用户对目标用户的贡献的缩放因子;in(u)表示可以影响目标用户u的用户的集合。
在FUSG模型中,具有较低的in-degree和较高的out-degree的用户更重要。在公式(7)中,影响更多用户并且受较少用户影响的用户具有较小PageRank值,PageRank值越小表明用户越重要。解决上述问题最简单的方法是使用单调递增函数来改进用户的PageRank值,如公式(8)所示:

但是,该方法生成的用户重要性值远大于其影响值,当将用户的影响值和重要性结合起来进行预测时,后者会在推荐过程中压制前者,减小前者对推荐质量的影响。非对称用户影响值的范围是[0,1],因此用户的PageRank值需要映射到[0,1],所以上述方法并不适用。本文模型采用逻辑回归函数将PageRank值映射到[0,1],如公式(9)所示:

根据非对称用户影响值和用户全局重要性值的乘积来对目标用户将在某兴趣点签到的概率进行预测。给定用户u,用户u将在兴趣点l签到的预测概率ĉul根据公式(10)得到:

其中,wvu表示用户v对用户u的影响值。
3.2 基于社交的影响
现实生活中,朋友之间具有较多的共同兴趣,例如:朋友经常一起去看电影等。为了充分利用社交影响,设计了一种融合社交关系和用户居住距离来计算用户间的社交影响[11,19]。一方面居住距离较近的朋友比距离较远的朋友分享更多的兴趣点;另一方面两个用户拥有的共同朋友越多,他们之间的共同兴趣也就可能越多。通过sigmoid函数将拥有社交关系的用户的居住距离转换为规范的相似性,同时,使用Jaccard相似度计算LBSNs中用户之间的相似性。使用超参数β来平衡上述两种相似性,则用户u和用户v之间的相似度sim(u,v)如公式(11)所示:
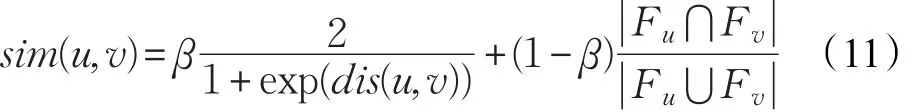
其中,Fu表示用户u的社交朋友集,v∈Fu,dis(u,v)表示用户u和用户v居住距离,超参数β∈[0,1]。用户u在兴趣点签到的预测概率r̂ul如公式(12)所示:

rvl表示用户v在兴趣点l签到的频率。
3.3 基于地理的影响
由图1可知用户在兴趣点签到的意愿与兴趣点之间的距离成幂律分布。使用幂律分布模拟用户从一个兴趣点移动到另外一个兴趣点的距离函数作为用户可能签到概率,如公式(13)所示:

其中,disl表示两个兴趣点之间的距离,wi(disl)表示用户访问距离disl远的兴趣点的概率,a和k是幂律函数的参数。
使用最大似然估计计算参数a和k,在公式(13)的两边取对数,得到公式(14):

通过最小二乘法获得公式(13)中的参数a和k。假设:用户在兴趣点li,他将要签到的兴趣点是lj,兴趣点li和兴趣点lj之间的距离为disl(li,lj)。用户将在兴趣点lj签到的概率与用户在距离disl(li,lj)处兴趣点签到的意愿wi(disl) 成比例。如公式(15)所示:

给定用户u和他签到历史的兴趣点集合Lu,基于贝叶斯公式预测用户在每个候选兴趣点的签到概率,然后向用户推荐概率较高的兴趣点。由公式(16)计算得到:

其中,P(l)是数据集中所有用户在兴趣点签到先验概率表示访问过兴趣点l的用户数目。
3.4 FUSG模型
融合用户偏好、社交信息和地理信息进行兴趣点推荐,提高兴趣点推荐系统的质量。用分别表示用户ui基于用户偏好、社交信息和地理信息模型下在兴趣点lj的签到概率,计算如公式(17)、(18)和(19)所示:

用Sij表示用户ui最终在兴趣点lj的签到的概率得分,即用户ui在兴趣点lj签到的可能性越大,则Sij越大。设、和分别表示用户基于用户偏好、社交信息和地理信息模型下的签到的概率得分,则Sij计算如公式(20)所示:

其中,、和分别由公式(21)、(22)和(23)计算获得:

其中,L表示所有兴趣点集合,Lu表示用户u签到过的兴趣点集合。
4 实验结果及分析
4.1 实验数据集
本文实验使用Gowalla公开的实际数据集[17]。数据集统计数据如表1所示,数据集包含196 591位用户、1 280 969个兴趣点、6 442 890次签到、950 327个社交关系链接、用户签到矩阵稀疏度为2.9×10-5、平均位用户签到37.18个兴趣点以及平均每个兴趣点有3.11次签到。在实验中,随机选取数据集中的20%作为测试数据集,剩余80%的数据集作为训练数据集。
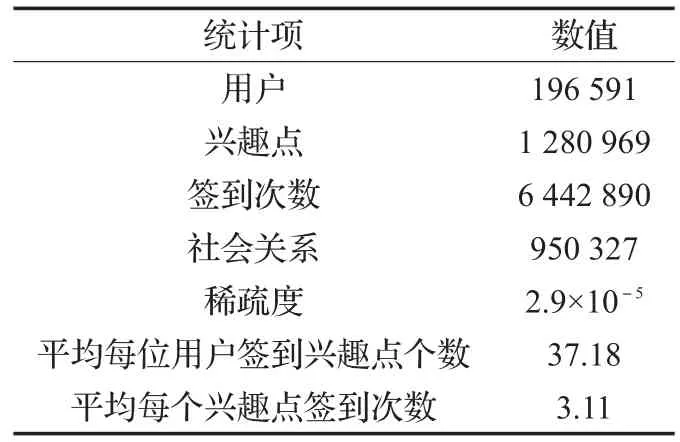
表1 Gowalla实验数据集
4.2 评价指标
在性能对比实验中,采用两种Top-N指标评估推荐的质量,精确率Precision@N和召回率Recall@N。衡量指标如公式(24)、(25)所示:
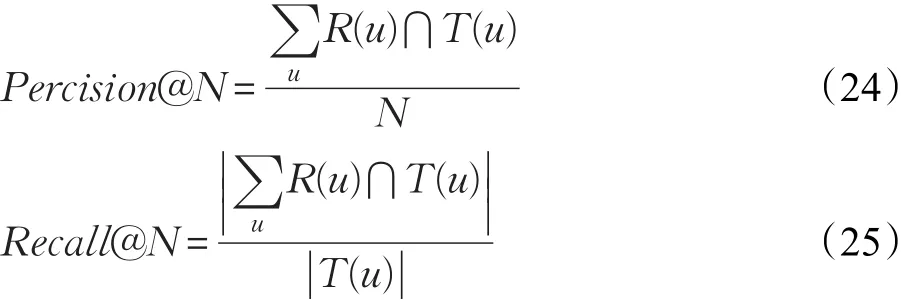
其中,N是推荐给用户的POIs的数量,T(u)是用户在测试集上的行为列表,R(u)是根据用户在训练集上的行为给用户做出的推荐列表。
4.3 参数分析
本节中,主要分析参数α和β对FUSG模型在数据集上对实验结果的影响。首先分析参数β,该参数在计算基于社交的相似度时在平衡两个用户间居住距离和用户朋友集合方面起着重要作用。图2和图3分别给出了参数β在[0,1]变化时,对推荐结果精确率和召回率的影响,其中Top-N个数为5。由图2和图3中可以发现FUSG模型的精确率和召回率随着参数的增加先增加后减少。当参数β等于0.5时,本文FUSG模型的Precision@5和Recall@5达到最高值,分别为0.13和0.07。当参数β为0.5时,模型推荐效果最佳。因此,本文实验中将参数β设置为0.5。

图2 参数β与精确率

图3 参数β与召回率
下面将分析参数α对FUSG模型性能的影响。参数α用于平衡非对称用户影响中用户的全局影响因子。固定参数β的值为0.5,参数α的值在[0,1]范围内变化。图4和图5分别给出了FUSG模型在参数α改变时的精确率和召回率,从图中可以看出模型的Precision@5和Recall@5随着参数α的增加而增加,当参数为1时,Precision@5和Recall@5达到最大值。因此,本章实验中设置参数α的值为1。

图4 参数α与精确率

图5 参数α与召回率
4.4 实验结果分析
为了验证本章FUSG模型在兴趣点推荐的性能,本节首先根据4.3节参数分析对参数进行设置。将参数α和β的值分别设为1和0.5。本章采用的对比模型如表2所示。下面为四种对比模型的详细介绍:
US模型:融合用户偏好和社交信息的兴趣点推荐(User preference and Social influence,US)。仅考虑FUSG模型中用户偏好和社交关系,计算方法为
UG模型:融合用户偏好和地理信息的兴趣点推荐(User preference and Geographical influence,UG)。选用了FUSG模型中的用户偏好和地理信息作为影响因
SGFM模型[19]:基于社交和地理影响的兴趣点推荐。该模型首先将用户偏好和基于社交的协同过滤融合到一个组合模型中,然后和地理信息影响结合在一起形成SGFM模型。
USG模型[11]:利用地理影响的协同兴趣点推荐。该模型将基于用户的协同过滤、基于社交的协同过滤和地理信息影响进行线性拟合,形成了USG模型。

表2 本文模型和对比模型
图6和图7分别为五种模型的精确率和召回率的实验对比结果。随着推荐Top-N数量的增加,模型的精确率整体呈下降趋势,召回率则呈现不断上升趋势。从图6和图7可知,本文所提出的模型在精确率和召回率上都明显优于其他四种对比模型。FUSG模型取得的显著进步表明融合多种因素兴趣点推荐的有效性。由于US仅仅考虑了用户偏好和社交信息的影响,而忽略了对兴趣点推荐影响最重要的地理信息,因此,在对比模型中该模型的精确率和召回率相对较低。在UG模型中使用地理信息代替了社交信息,充分利用用户的地理信息,虽然比US模型在精确率和召回率上有了一定的提高,但是优于使用的影响因素相对较少,没有使用到用户的社交信息。因此,在提高兴趣点质量上有一定的限制。SGFM模型中虽然使用了用户偏好、社交信息和地理信息三种影响因素,但是由于在考虑用户偏好时,认为两个用户之间的影响是对称的;在社交信息中计算用户相似度时仅考虑了用户的朋友集合,没有考虑用户之间的居住距离等信息,并且计算地理影响是存在一定的不足。USG模型在计算用户偏好时存在与SGFM模型相同的不足,但是在社交关系中计算用户相似度时,不仅考虑了用户的朋友集合,而且还将用户签到的兴趣点集合融入到相似度中,在一定程度上提高了社交关系的影响,在挖掘地理信息影响时使用幂律分布来挖掘地理信息对兴趣点推荐系统的影响,该方法优于SGFM模型中的地理信息影响。根据图6和图7可以看出,UG模型明显优于US模型,该实验结果表明,用户更喜欢访问他历史签到兴趣点附近的兴趣点,而不是他的社交朋友们喜欢签到的兴趣点,即地理信息在提高兴趣点推荐性能上优于社交关系的影响。
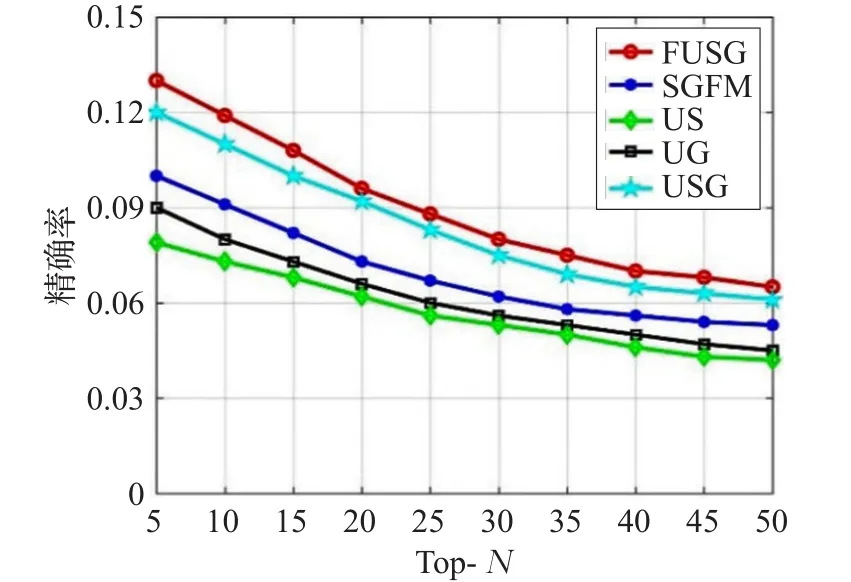
图6 五种模型精确率对比

图7 五种模型召回率对比
5 结论与展望
本文提出的FUSG模型,能够充分地利用用户的签到历史、社交信息和地理信息。同时,提出了利用朋友间的居住距离和朋友集合来求解社交关系中的用户相似度;最后融合地理信息得到推荐结果。通过在真实的Gowalla数据集上的实验结果,表明本文的FUSG模型在提高兴趣点推荐型性能上有了一定的提高,能够为用户提供更准确的参考。
在现实生活中时间信息对人们的签到行为有着重要的影响,一方面是由于用户在时间维度上具有一定的规律性和周期性;另一方面兴趣点在提供服务时有一定的时间限制,如:饭店和博物馆的营业时间等。如果在FUSG模型中能够融入时间影响将会获得更好的推荐效果。
