光子晶体的透射特性

潘 庆, 张晓茹, 刘 晗, 杨涪铨, 刘继平, 孟祥东, 吴向尧, 郭义庆

(1. 吉林师范大学 物理学院, 吉林 四平 136000； 2. 中国科学院 高能物理研究所, 北京 100049)

当光子在具有不同介电常数呈周期性排列的材料中传播时, 其传播行为可被改变, 这种材料称为光子晶体[1-2]. 光子晶体具有光子带隙、 缺陷态和光的局域态等特征. 利用这些特征可制备高效率半导体激光器、 发光二极管、 波导、 光学滤波器、 高Q谐振器、 天线、 光学波导[3-6]、 光学限幅器和放大器等[7-9].

目前, 理论研究光子晶体的方法主要有： 平面波展开法、 传输矩阵法和时域有限差分法等[10-13], 这些方法均来源于经典Maxwell方程, 即经典电磁理论方法. 本文提出一种研究一维光子晶体的量子理论方法, 利用该方法给出光子在一维光子晶体自旋波函数的形式, 进一步计算得到量子传输矩阵、 量子色散关系、 量子透射率和反射率. 在数值分析中, 计算不同结构一维光子晶体的量子色散关系、 量子透射率和反射率, 分析周期数对光子晶体量子透射率的影响, 并将量子理论方法与经典电磁方法的计算结果进行比较. 结果表明, 其计算结果一致. 量子理论方法可用于研究二维和三维光子晶体, 并可进一步研究光子晶体的量子拓扑性质.

1 光子的自旋波动方程

自由和非自由光子的自旋波动方程[14]分别为

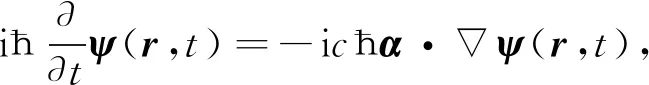
(1)

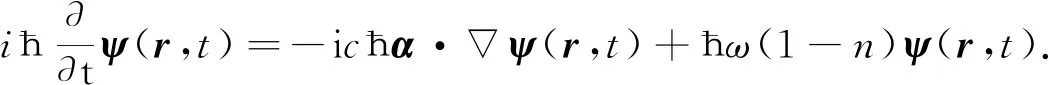
(2)

在折射率为n的介质中, 光子的势能为V=ħω(1-n)[15], 光子的自旋波函数ψ和α矩阵的三维分量形式分别为

(3)

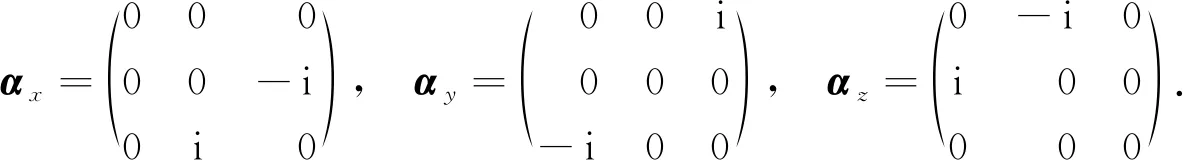
(4)

利用分离变量法ψ(r,t)=ψ(r)f(t), 方程(1),(2)可变为

-icħα·ψ(r)=Eψ(r)，

(5)

-icħα·ψ(r)+ħω(1-n)ψ(r)=Eψ(r),

(6)

其中E为光子在介质中的总能量. 方程(2),(6)分别为光子在介质中含时与不含时的量子波动方程, 由该方程可研究光在一维光子晶体介质中的量子透射特性.

2 一维光子晶体的量子传输矩阵

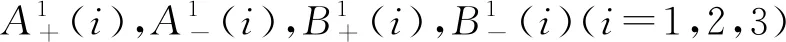
图1 一维光子晶体(AB)N的量子结构

由方程(2),(6)可得光在介质A,B中入射和反射的平面波解分别为

在真空区域的总入射波函数由入射部分和反射部分叠加组成：

(9)

其中:F1,F2,F3表示光子入射波函数的振幅分量;F4,F5,F6表示光子反射波函数的振幅分量.

类似地, 可写出第二周期和第N周期的光波函数：

其中:

θ为在真空区域的入射角.

根据波函数及其一阶导数在x=0处连续, 利用方程(7),(9)可得：

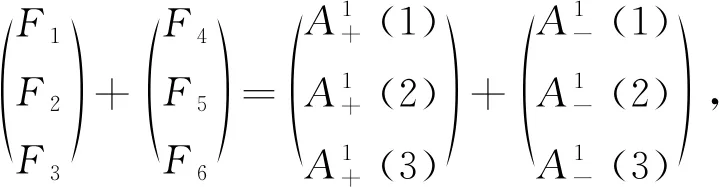
(14)

(15)

方程(14),(15)可写成如下矩阵形式：

(16)

其中:

通过计算可见, 每个介质层A和B间均可写出传输矩阵MA和MB, 且在不同周期内A和B介质的传输矩阵相同.MA和MB分别为

(17)

其中:

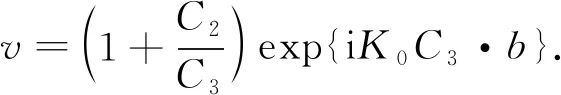
M0,MA,MB称为量子传输矩阵.

对于第N周期的一维光子晶体, 量子透射波函数可写为

(18)

根据波函数及其一阶导数在x=N(a+b)处连续, 利用方程(13),(18)可得

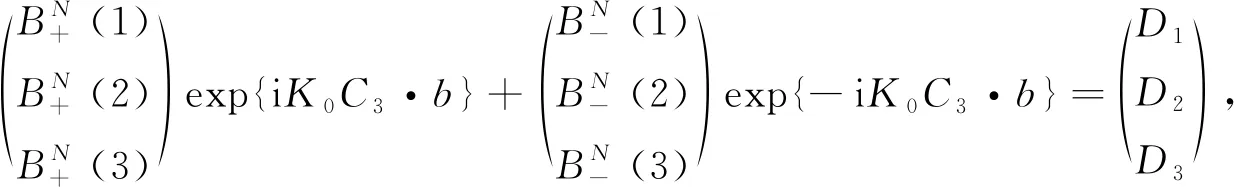
(19)

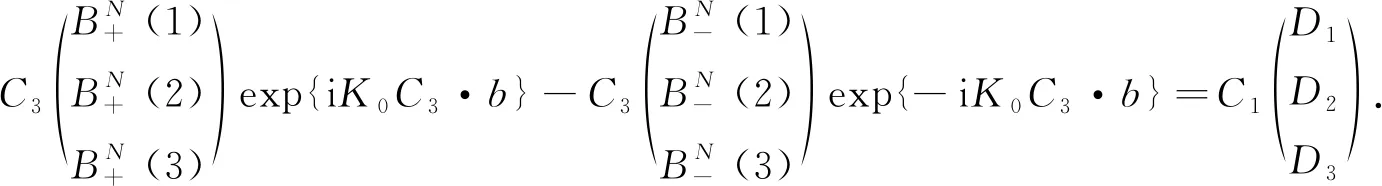
(20)

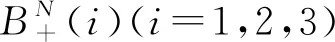
(21)

由方程(5)可得一维光子晶体(沿x方向传播的平面波)的透射率T和反射率R分别为

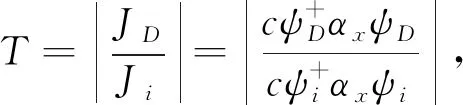
(22)

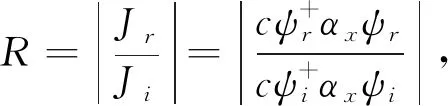
(23)

其中:

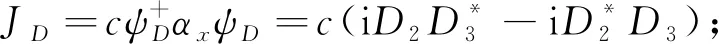
(24)

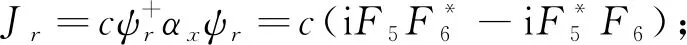
(25)

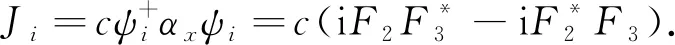
(26)

通过计算可得

(27)

(28)

其中:

Q2=M51N1+M52N2+M53N3;

Q3=M61N1+M62N2+M63N3;

Δ=M11M22M33-M11M23M32-M12M21M33+M12M23M31+M13M21M32-M13M22M31;

由Bloch定理可得

将式(29),(30)代入方程(7),(8),(10),(11)可得

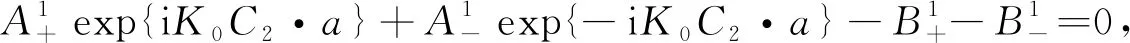
(31)

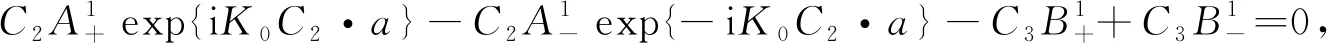
(32)

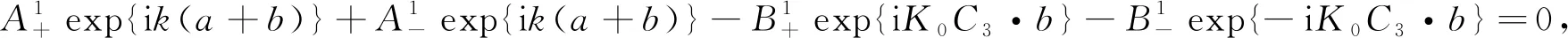
(33)

方程(31)～(34)的非零解为

(35)

由方程(35)可得一维光子晶体的量子色散关系式为

(36)

3 结果与讨论

一维量子光子晶体的初始参数如下： 介质A和B的折射率分别为nA=1.6,nB=2.97, 厚度分别为a=277 nm,b=130 nm, 入射角为θ=0, 中心频率为ω0=271 THz. 一维光子晶体结构为(AB)N, 其中N为周期数. 将上述参数代入方程(27),(28),(36)可得量子透射率、 量子反射率和量子色散关系曲线, 并与经典透射率、 经典反射率和经典色散关系进行比较. 一维光子晶体(AB)8的色散关系曲线如图2所示, 其中： 图2(A)为量子色散关系; 图2(B)为经典色散关系. 由图2可见, 在量子和经典色散关系曲线中, 禁带宽度、 位置和通带均相同.

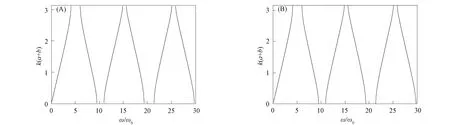
图2 一维光子晶体(AB)8的色散关系

一维光子晶体(AB)8的透射率关系曲线如图3所示, 其中: 图3(A)为量子透射率; 图3(B)为经典透射率. 由图3可见, 在量子和经典透射率曲线中, 禁带位置和宽度均相同. 一维光子晶体(AB)8的反射率曲线如图4所示, 其中： 图4(A)为量子反射率曲线； 图4(B)为经典透射率曲线. 由图4可见, 量子和经典反射率关系曲线相同. 一维光子晶体(AB)16的透射率曲线如图5所示, 其中图5(A)为量子透射率曲线; 图5(B)为经典透射率曲线. 由图5可见, 量子和经典透射率曲线相同. 比较图3和图5可见: 当周期数N=8时, 在ω/ω0=15和ω/ω0=26附近, 禁带不明显(透射率T≠0); 当周期数N=16时, 在ω/ω0=15和ω/ω0=26附近, 禁带较明显(透射率T=0), 且随着周期数N的增大, 通带变密, 即态密度变大. 因此周期数影响光子晶体的禁带和态密度.

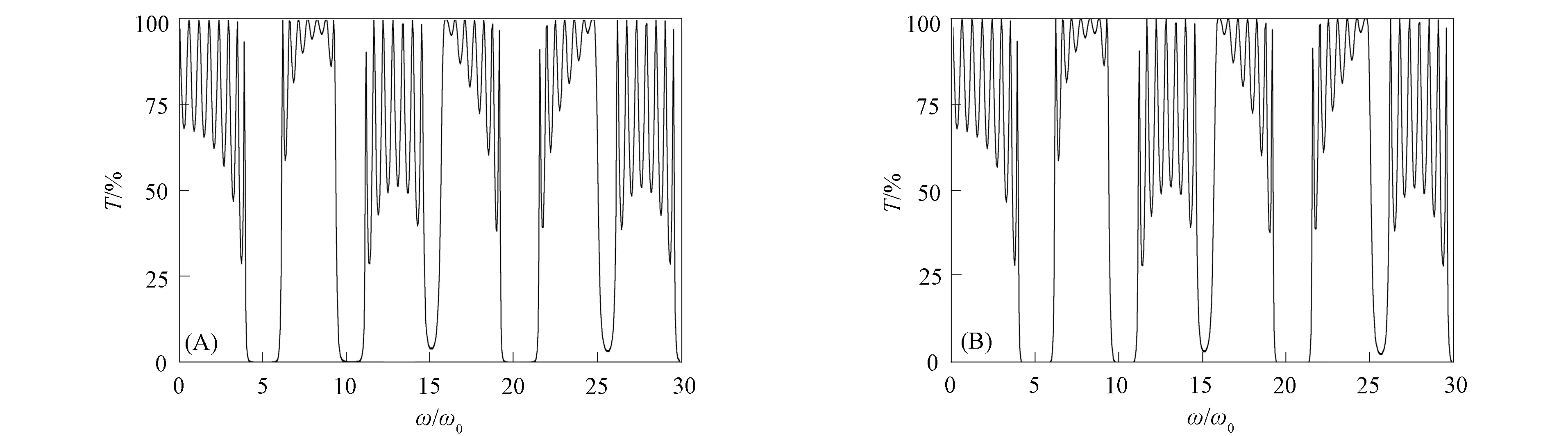
图3 一维光子晶体(AB)8的透射率

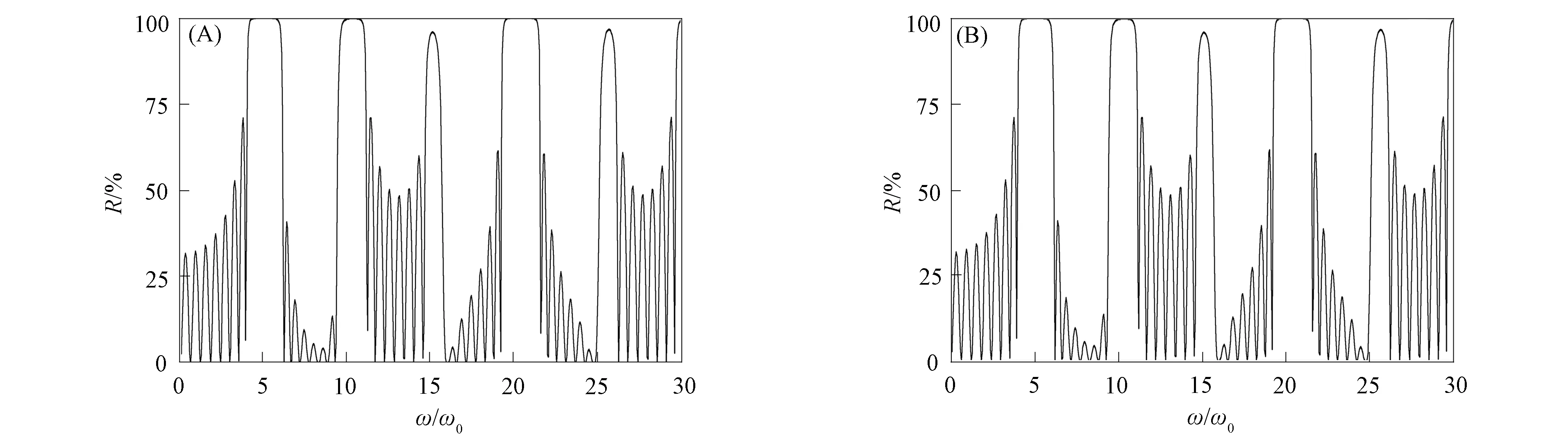
图4 一维光子晶体(AB)8的反射率

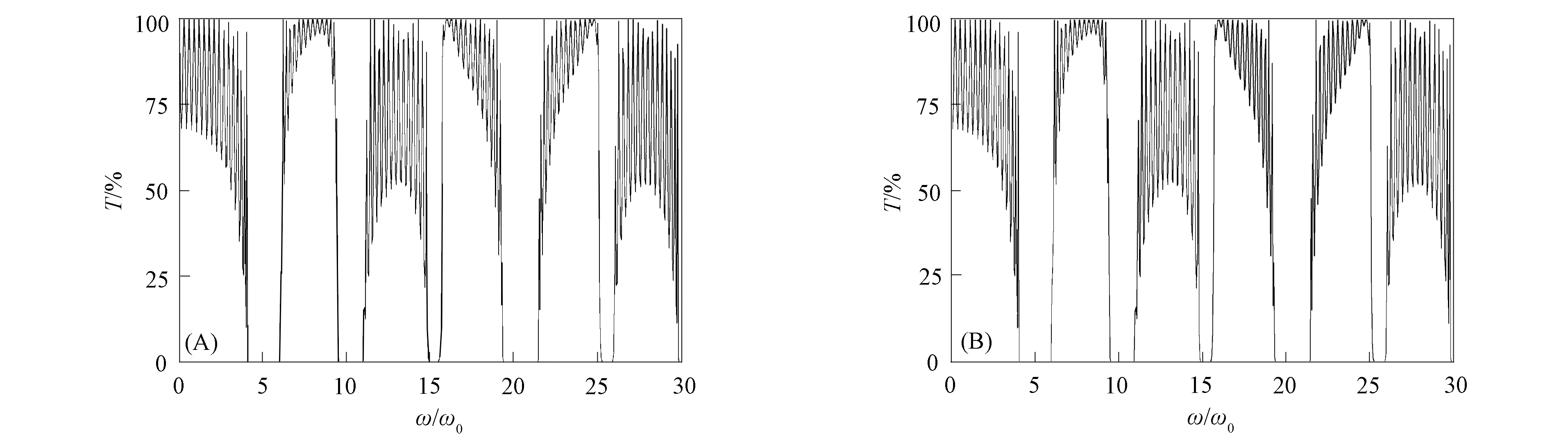
图5 一维光子晶体(AB)16的透射率

综上所述, 本文用光的量子理论方法研究了光子晶体色散关系、 透射率和反射率, 与光的经典理论方法所得结果完全相同, 表明该量子理论方法正确. 该方法可进一步用于研究光子晶体的量子Zak相位、 量子陈数和量子边缘态等量子拓扑性质.