热源参数识别问题的Bayes遗传算法
2020-07-17尹伟石刘晓奇
尹伟石, 刘晓奇, 徐 轩
(长春理工大学 理学院, 长春 130022)
热传导反问题在航空航天、 核能工程、 医疗检测等领域应用广泛. 在热传导正问题中, 温度场是在物体热物性系数、 边界条件和初始条件已知的情况下, 由一些数值算法求解得到, 常用的方法有差分法、 边界元法[1]等; 在热传导反问题中, 先已知温度观测值, 然后用已知观测值对未知的热参数等条件进行求解, 常见的方法主要有正则化方法[2-3]、 有限元[4]、 遗传算法[5]等. 热源参数识别问题作为热传导反问题的一个重要研究方向, 目前已被广泛关注. 例如: Yang等[6]利用Tikhonov正则化方法对空间热源问题进行了求解; Shah等[7]利用共轭梯度法结合伴随问题对一维热传导方程的瞬时热源进行了反演; Lee[8]将排斥粒子群算法应用于热传导反问题的热源参数估计. 近年来, 随着计算机技术的发展, 以Bayes推理为基础的热传导反问题求解方法备受关注. 例如: Zeng等[9]提出了一种非参数总体Monte Carlo的自适应Bayes近似计算方法, 用于线性和非线性热传导反问题的计算; Silva等[10]利用Bayes滤波器和Markov链Monte Carlo方法对时变边界热流进行了估计; Jakkareddy等[11]利用Bayes方法结合液晶热像仪对自然对流中的局部换热系数进行反演. 本文利用Bayes遗传算法对热源位置和产生时间参数进行求解.
1 正问题
二维瞬态热传导问题的控制方程可表示为
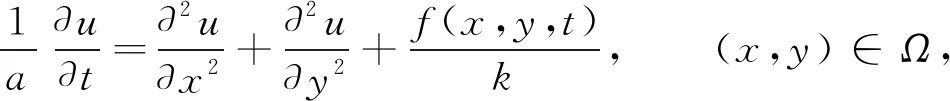
(1)
其中:u表示温度;x,y表示空间坐标;Ω表示求解域;k表示导热系数;a=k/(ρc)表示热扩散系数,ρ和c为常数, 分别表示材料密度和比热容;t表示时间;f(x,y,t)为Ω内的瞬时热源, 大小随时间变化. 该问题的边界条件和初始条件分别为
其中:Γ1和Γ2表示边界,Γ1∪Γ2=Γ,Γ1∩Γ2=Ø;n表示边界Γ的外法向量.
2 Bayes遗传算法
2.1 Bayes理论
Bayes公式为
式中:p(α|d)为参数的后验概率密度函数,α为模型参数,d为观测数据;p(α)为参数的先验密度函数;P(d|α)为条件概率密度;p(d)为积分常数.
根据Bayes公式可得参数的后验概率密度函数. 本文研究的未知参数后验概率密度函数[12]为
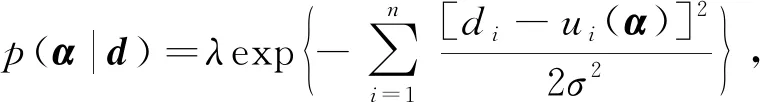
(5)
式中:α=(α1,α2,…,αm)为模型未知参数, 共有m个;d=(d1,d2,…,dn)为观测值, 共有n个;ui(α)表示与参数α相对应的第i个预测值,εi=di-ui(α)表示测量误差,i=1,2,…,n, 并且假设观测误差服从均值为零、 标准差为σ的正态分布N(0,σ2), 且相互独立;λ为常数, 与参数α无关.
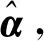
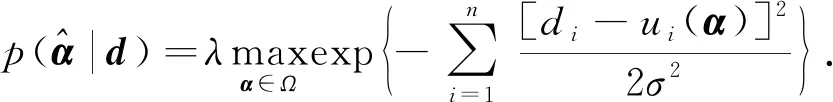
(6)
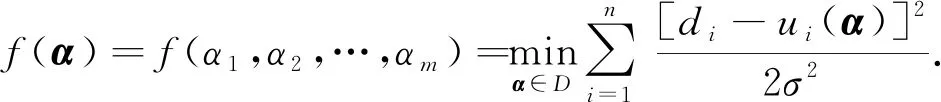
(7)
由于式(7)中的数据通常都是高维的, 因此其形式非常复杂, 直接对其进行计算很困难, 本文利用遗传算法对式(7)进行刻画, 进而得到式(6)的最大后验概率密度.
2.2 遗传算法
遗传算法是一种具有全局寻优能力的自适应算法, 其用种群作为函数解, 算法具有高效、 实用、 稳定性强的特点, 可以有效地用于解决非线性、 多峰值、 多目标函数等问题. 遗传算法包括适应度计算、 选择、 交叉、 变异4个步骤, 其中, 交叉是群体即解的信息随机交换的过程, 变异是对解添加随机扰动的过程.
1) 适应度计算: 把目标函数作为适应度函数, 计算每个个体的适应度值.
2) 选择: 选择是根据个体适应度值, 对有效解个体进行一定比例的选择保留. 本文求解的问题是使式(6)达到最大, 因此, 在计算过程中需按一定比例保留使适应度值达到最大的个体, 被保留的这些个体称为有效解, 复制这些解使其传递到子代.
在选择过程中, 有多种选择策略, 常用的是轮盘赌法. 轮盘赌法是依概率按照Monte Carlo法对每个个体进行选取, 在选取过程中, 可以对个体的适应度值进行线性缩放, 即种群中最差个体的目标函数值减去种群中每个个体的目标函数值:
fj=max{uj|j=1,2,…,m}-uj.
(8)
在选择过程中, 每个个体的选择概率可根据适应度值确定:

(9)
为有效减轻选择比例的压力, 减小算法早熟的问题, 可采用排序选择策略, 其基本思想是: 将M个个体的适应度值按从小到大的升序进行排列, 记为1,2,…,m, 排序后的个体被选择概率为
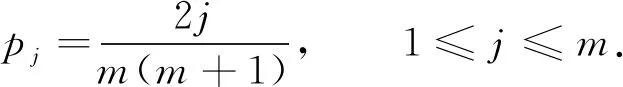
(10)
3) 交叉: 交叉是对选中的一对候选解, 将其所包含的信息按一定的概率进行交流互换的过程, 该过程是随机的, 用公式表示为
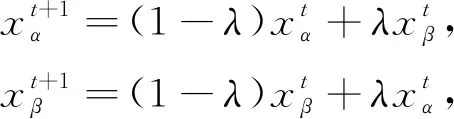
(11)
4) 变异: 变异是对交叉后的种群进行随机扰动, 用公式表示为
xj,D+1=xr1,D+F(xr2,D-xr3,D),
(12)
其中:xj,D+1,xr1,D,xr2,D,xr3,D为解个体;r1,r2,r3∈{1,2,…,Np},Np为种群数目;D为进化代数;F∈[0,1]为变异因子. 变异是为提高遗传算法对解空间局部搜索能力, 丰富种群多样性, 增大其达到全局最优可能而进行的操作, 变异通常是以非常小的预定概率进行的.
通过上述分析, 可得Bayes推理与遗传算法相结合用于热源参数识别问题的求解步骤如下:
1) 根据Bayes原理和热传导方程确定目标函数;
2) 根据待估参数的先验信息确定参数的取值范围;
3) 初始化产生一定规模的种群, 即初始解;
4) 计算每个个体的适应度值;
5) 根据合适的选择策略对种群进行选择保留;
6) 选择适合的交叉策略, 对保留的种群进行交叉操作;
7) 根据相应的变异策略对种群进行变异操作;
8) 执行终止判断准则, 如果满足终止准则, 则选择适应度值高的个体作为参数识别问题的最终解, 停止计算; 否则, 返回步骤4), 继续计算, 直到满足终止判别条件为止.
3 数值算例
下面以包含瞬时热源的二维热传导方程为例, 分析Bayes遗传算法的反演效果.
3.1 实 例
对于二维热传导方程:

(13)
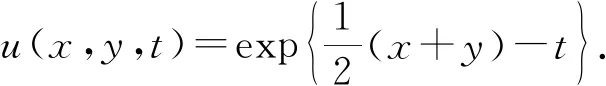
假设热源为瞬时热源, 建立热源的二维热传导模型. 设热源在坐标中心处, 热源产生的时刻记为t=0, 观测点B的位置为(x0,y0), 首次测量时刻为热源产生后的t0时刻, 则待反演参数的真实解为α=(x0,y0,t0). 取热源参数真实值横坐标x0=0.35 m, 纵坐标y0=0.55 m, 第一次检测距热源开始时间t0=0.3 s. 用x,y,t作为参数真实值x0,y0和时刻t0的估计值, 记为α1=(x,y,t).
设从首次测量开始后每隔0.02 s测量一次, 直到0.68 s, 利用热源参数真实值和式(13)计算得观测点B的温度值, 共20个计算数据, 结果列于表1.

表1 观测点不同时刻测量的温度值
3.2 Bayes遗传算法的参数反演结果
根据上述数据, 利用Bayes遗传算法对热源参数进行估计. 根据正问题的先验信息, 得到α1的分布范围, 其中每个参数都服从均匀分布, 且相互独立, 然后根据Bayes定理, 由式(5)得模型后验概率密度函数为
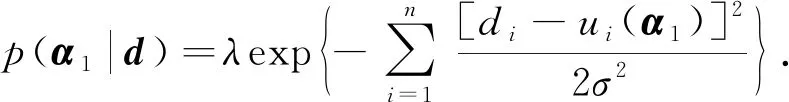
(14)
设种群规模Np=100, 交叉率为Pc=0.9, 变异率Pm=0.1, 按照遗传算法迭代50次达到稳定, 参数的估计值为:x=0.351,y=0.551,t=0.301.
Bayes遗传算法迭代300次得到参数x,y,t的后验概率直方图和迭代曲线分别如图1和图2所示, 其中, 参数x,y,t的后验概率大小分别用p(x),p(y),p(t)表示.
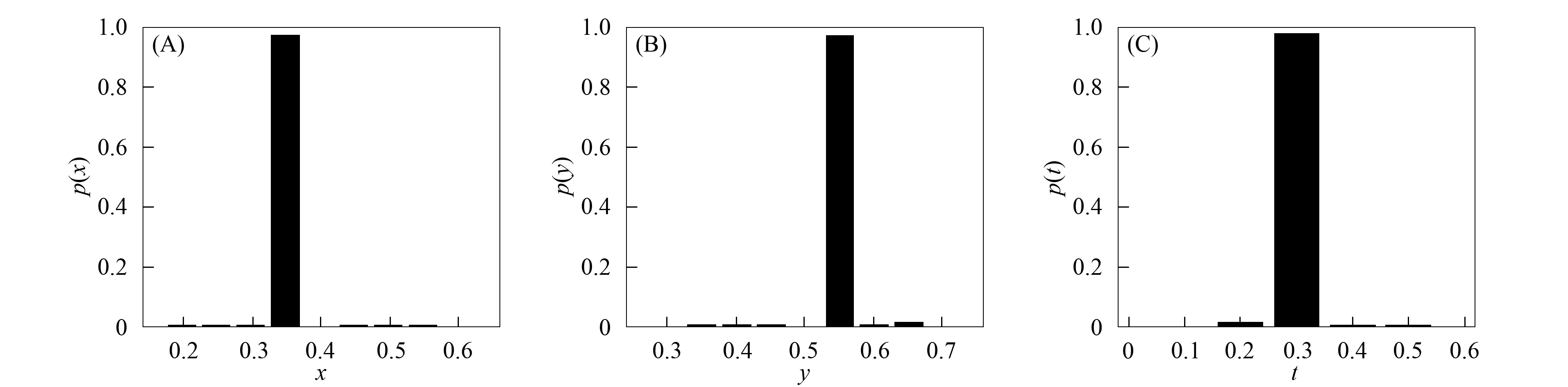
图1 基于Bayes遗传算法的模型参数后验概率直方图
由图1可见, 参数x,y,t的后验概率分布呈近似正态分布, 并且分别在0.35,0.55,0.3附近频率达到最大. 由图2可见, 当迭代次数超过50次时, 参数x,y,t稳定地收敛到参数真实值附近.
3.3 反演结果对比
作为对比实验, 采用Bayes微分进化算法对模型参数进行求解, 得到参数x,y,t的反演结果如图3所示. 由图3可见, 当迭代次达到130次时, 参数x,y,t稳定地收敛到参数真实解附近, 结合上述对Bayes遗传算法收敛速度的分析, 可知Bayes遗传算法的收敛速度更快.

图2 基于Bayes遗传算法的模型参数迭代曲线
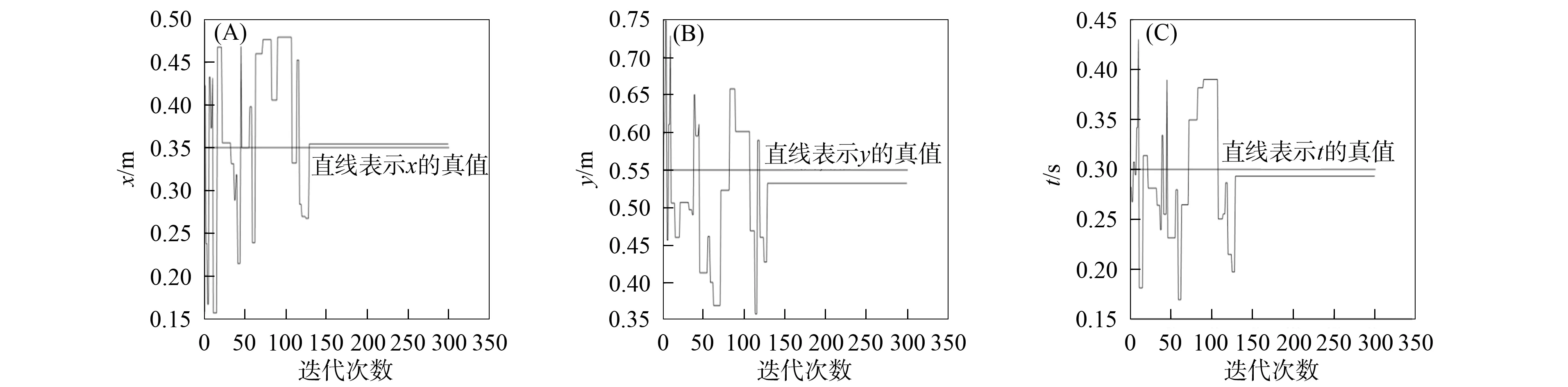
图3 基于Bayes微分进化算法的模型参数迭代曲线
为进一步分析Bayes遗传算法的反演效果, 从Bayes遗传算法的反演结果中剔除前50次不稳定的结果, 只对后250次反演结果进行统计分析; 同理, 剔除Bayes微分进化算法前130次不稳定的反演结果, 只对后170次反演结果进行统计分析, 统计结果列于表2. 由表2可见, Bayes遗传算法得到参数x,y,t的均值误差都在1%以下, Bayes微分进化算法得到参数x,y,t的均值误差在4%以下, 说明与Bayes微分进化算法相比, Bayes遗传算法的反演精度更高.

表2 Bayes遗传算法与Bayes微分进化算法的模型参数后验统计结果比较
为验证Bayes遗传算法的稳定性, 先对测量数据分别添加5%和10%的噪声, 然后对反演结果每隔10个点取一个值, 得到参数x,y,t序列的相对误差和统计分析结果, 分别如图4和表3所示.
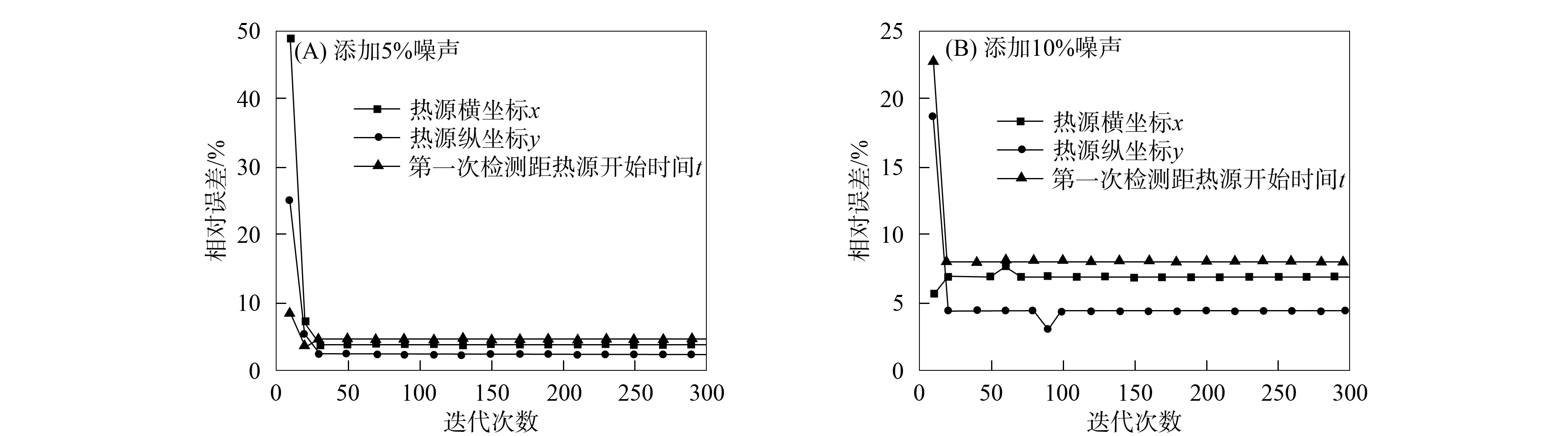
图4 Bayes遗传算法在不同噪声下的参数反演相对误差序列

表3 Bayes遗传算法在不同噪声下参数反演的统计分析结果
由图4可见, 对观测数据分别添加5%和10%的噪声, 参数的相对误差均控制在9%以下. 由表3可见, 当对观测数据添加5%的噪声时, 参数的均值误差都控制在2%~5%, 当对观测数据添加10%的噪声时, 参数的均值误差都控制在4%~9%, 说明Bayes遗传算法具有较好的稳定性.
综上可见, Bayes遗传算法用概率语言对参数信息进行描述, 算法具有较好的稳定性, 能有效地对热源参数进行估计, 为基于Bayes方法的热传导反问题提供了一种新的计算方法.
