压水堆堆芯Pin-by-pin计算广义等效均匀化方法研究①

张斌 李云召 吴宏春 刘勇 王冬勇 王星博 钟旻霄

(1.中国核动力研究设计院核反应堆系统设计技术重点实验室 四川成都 610213；2.西安交通大学核科学与技术学院 陕西西安 710049)

20世纪70年代以后，得益于粗网节块法[1,2]的迅速发展，以组件均匀化理论[3,4]和粗网节块方法为理论框架的两步法计算方案逐渐成为了压水堆工程计算中普遍采用的燃料管理中子学数值计算方法。伴随着粗网节块法的大量工程应用，适用于组件均匀化的均匀化理论得到了长足的发展。基于均匀化一般原理，结合早期有限差分堆芯计算的传统均匀化方法，Kord Smith基于等效均匀化理论提出了能够用于工程计算的广义等效均匀化方法[5]，即在等效均匀化参数中引入不连续因子以达到各节块的守恒条件，此化方法很好地满足了绝大部分商用压水堆的工程应用需求。

随着科学研究的不断深入、计算条件和对核设计计算精度要求的不断提高，传统的两步法计算方案面临着越来越严峻的挑战。为提高堆芯设计计算精度且满足对新型反应堆堆芯计算的精度要求，基于均匀化理论的改进型两步法计算方案全堆芯Pin-by-pin计算成为了下一代堆芯数值计算方法的研究热点。全堆芯Pin-by-pin计算减少了堆芯计算过程中的近似与假设，能够更加精细地考虑堆芯布置的非均匀性，直接求出单棒功率分布，便于堆芯燃料管理计算和相应的堆芯安全分析。

区别于组件均匀化的广义等效均匀化方法，Pin-bypin均匀化计算中，不连续因子的计算[6]不仅与非均匀介质本身及其所处环境有关，也与堆芯计算方法相关。本文研究了广义等效均匀化方法在压水堆堆芯Pin-by-pin计算中的理论模型，针对矩形指数函数展开扩散方法和SP3方法推导了零阶不连续因子和二阶不连续因子的计算公式，通过SP3方程形式构造伪固定源问题解决了高阶输运方程无法提供SP3方程中二阶中子通量密度的问题，并分析了压水堆堆芯Pin-by-pin计算中应用Pin-by-pin不连续因子的堆芯计算精度。

1 不连续因子的计算方法研究

广义等效均匀化方法通过放宽节块表面中子通量密度这一约束条件，来实现反应率及中子泄漏率的守恒，并提出了新的节块与节块之间的边界条件，即均匀化后堆芯内界面上中子通量密度乘上不连续因子后保持连续，第i节块第g能群的不连续因子定义式如下：

式中：f——不连续因子；s——节块表面；——节块非均匀中子面通量，单位（cm2·s）-1；——节块均匀中子面通量，单位（cm2·s）-1。

在栅格计算中，由高阶输运计算可以直接求得各个栅元各表面的非均匀中子面通量：

而栅元均匀中子面通量的计算方法则必须要与下游堆芯计算中所使用的中子学求解方法保持一致。

1.1 矩形指数函数展开扩散方法

本文堆芯低阶输运计算采用矩形指数函数展开节块方法，在矩形节块中，中子通量密度解析解取六阶近似，展开方向为各坐标轴的正负方向，则：

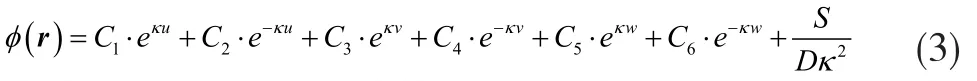
式中：Ci——展开系数；S——中子源项；D——扩散系数；Σr——移出截面；在保证右手系的前提下，。

公式(3)中的六个积分常数可由包含节块平均中子通量密度和节块五个边界面上净中子流密度（以出射流为正）在内的六个定解条件确定。

当堆芯中子学计算采用指数函数展开扩散方法求解时，根据公式(3)和表面出射中子流密度的定义式，可以得到指数函数展开节块方法内第i节块第g能群入射中子流密度与出射中子流密度之间的响应关系，以u+方向为例：

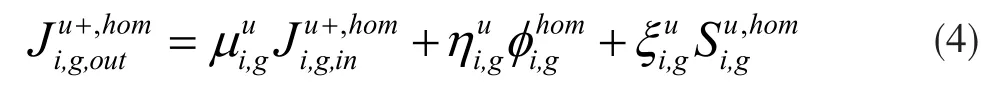
式中：h——栅元长度，单位cm；out——出射中子流；in——入射中子流；——系数；S——中子源。

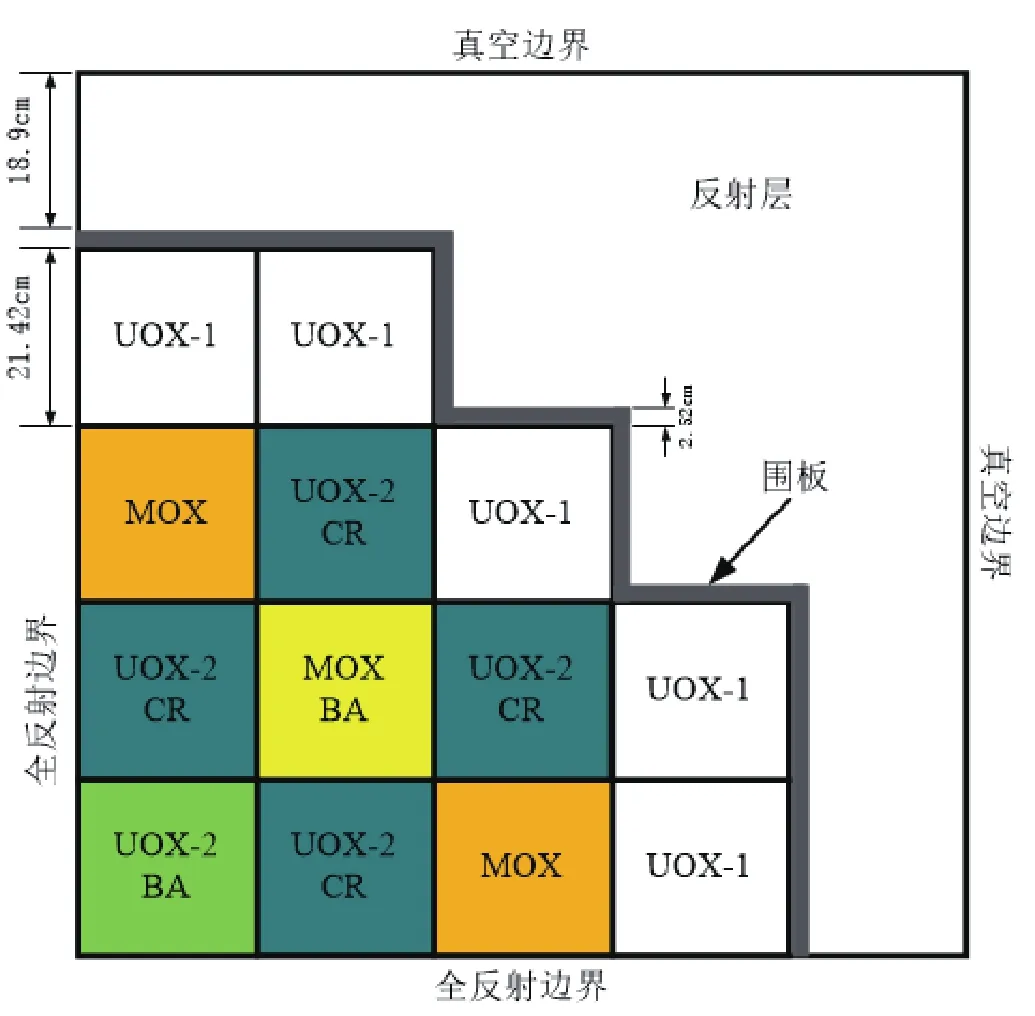
图1 KAIST基准题二维全堆芯布置和几何结构

图2 KAIST基准题二维全堆芯棒功率分布

根据菲克定律中栅元中子面通量、栅元净中子流密度与出射入射中子流密度的关系可以得到如下关系式：

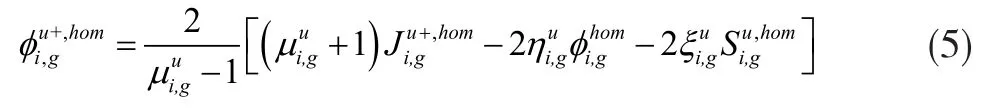
根据均匀化前后特征值、各能群反应率及中子泄漏率守恒，则在单组件栅格计算中有如下等式：

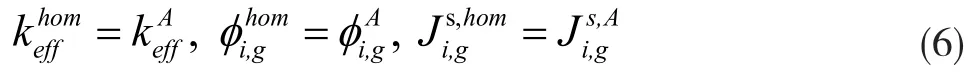
联立公式(5)和公式(6)：

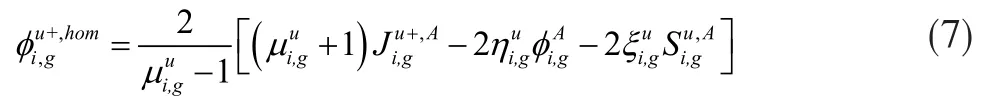
联立公式(1)、公式(2)和公式(7)即可求出指数函数展开扩散方法下栅元的不连续因子。

1.2 矩形指数函数展开SP3方法

当堆芯中子学计算采用矩形指数函数展开SP3方法求解时，通过与扩散方法中相似的推导，根据均匀化前后特征值、各能群反应率及中子泄漏率守恒，零阶均匀化面通量与二阶均匀化面通量表示如下：

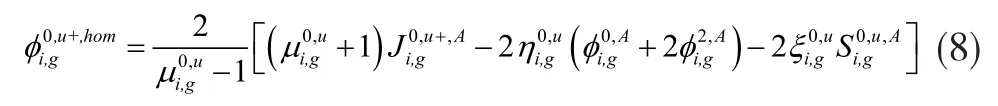
图3 组件均匀化粗网节块计算的棒功率误差分布

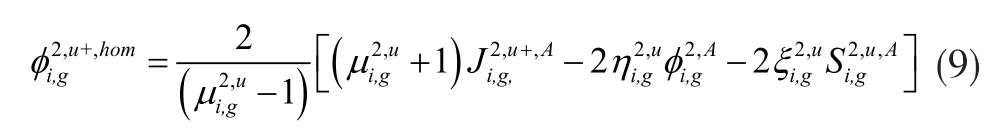
栅格非均匀一步法计算通常采用高阶输运方法进行计算，公式(8)和公式（9）中非均匀零阶中子通量密度和零阶中子流密度即为栅格输运计算直接获得，但非均匀二阶中子通量密度和二阶中子流密度无法无法由栅格计算直接提供。根据SP3方程的形式，非均匀二阶中子通量密度矩可由公式(10)计算得到。通过高阶输运的栅格计算得到非均匀零阶中子通量密度和零阶中子流密度，根据公式(10)右端项构造零阶中子通量密度的泄漏项作为该方程的固定源项，通过求解此伪固定源问题即可近似求得非均匀二阶中子通量密度和二阶中子流密度。

通过伪固定源方法近似求解出栅格计算中的非均匀二阶中子通量密度和二阶中子流密度后，根据公式(8)和公式(9)可以求出各阶栅元均匀中子面通量。需要注意的是二阶面通量的数值很小，且数值有正有负，而伪固定源方法是种近似方法，若按照不连续因子的定义式(1)进行SP3方程中二阶通量的不连续因子的求解会出现很大的数值甚至是负值。不合理的不连续因子会导致全堆芯SP3方程迭代求解时的不收敛。为避免出现这种情况，对二阶中子通量密度的不连续因子的求解关系式重新定义如下：

式中：s——节块表面。

根据公式(1)和公式(11)可以得到SP3方程中零阶和二阶不连续因子，相应地，在SP3方法进行全堆芯Pin-by-pin计算求解时，节块内部边界的耦合条件应为（以u方向为例）：

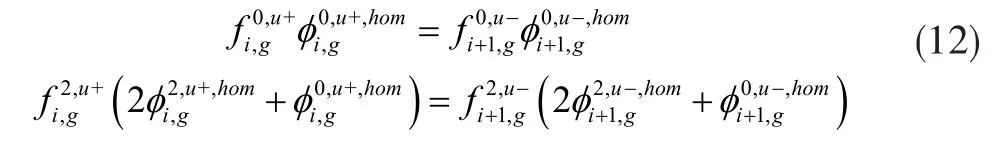
2 计算结果分析

为验证超级均匀化方法在压水堆堆芯Pin-by-pin计算中的计算精度，本节以KAIST基准题2A问题[7]下的二维全堆芯问题进行验证与分析，堆芯布置和几何结构如图1所示。

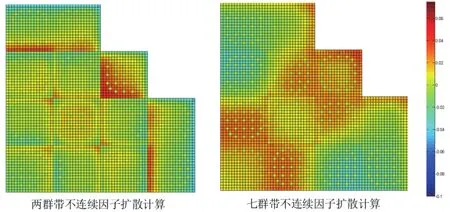
图4 堆芯Pin-by-pin扩散计算的棒功率相对误差分布

图5 堆芯Pin-by-pin SP3计算的棒功率相对误差分布

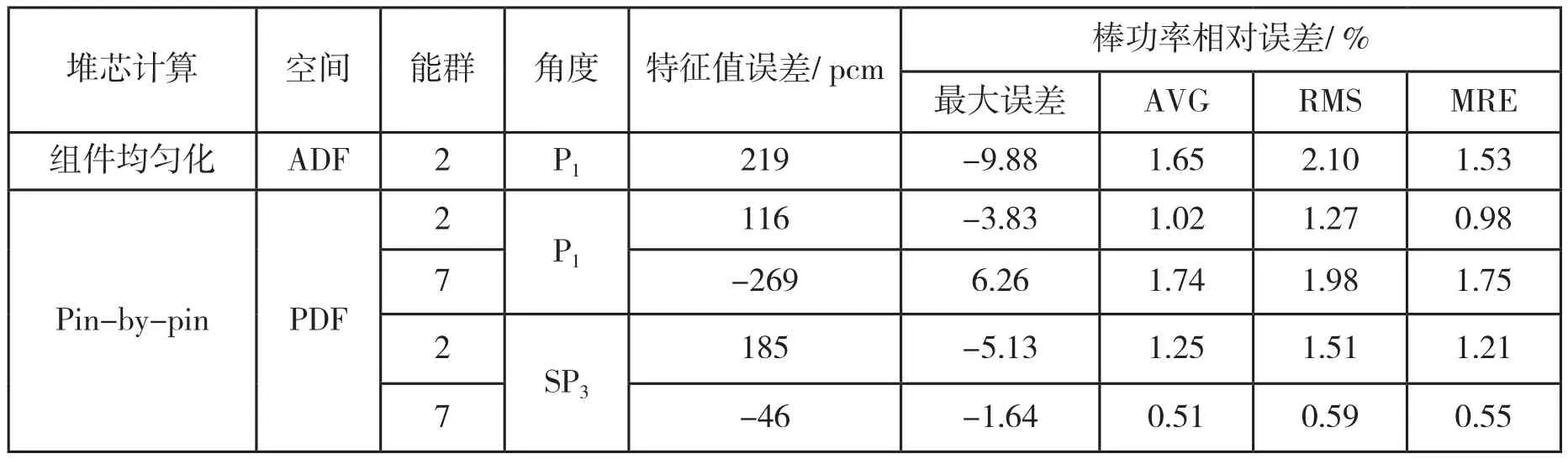
表1 堆芯两步法计算的特征值误差和棒功率误差

采用堆芯Pin-by-pin计算和堆芯组件均匀化粗网计算两种方案进行堆芯计算并加以分析和比较：

（1）依据广义等效均匀化理论模型，针对扩散方法（P1）和简化球谐函数方法（SP3）利用栅元不连续因子（PDF）分别产生两群和七群的等效均匀化少群常数，并在指数函数展开节块法中进行全堆芯Pin-by-pin计算；

（2）根据传统组件均匀化计算方法，产生两群带组件不连续因子（ADF）的组件等效均匀化常数并采用先进变分节块方法进行堆芯计算。变分节块方法在空间处理上直接针对中子通量密度分布进行离散，因此不需要功率重构过程而能直接得到中子通量密度分布，通过形状因子的求解即可得到堆芯棒功率分布。

二维堆芯参考解由Bamboo-Lattice2.0一步法计算获得，特征值参考解为0.97948，棒功率分布如图2所示。堆芯两步法计算的特征值误差和棒功率误差如表1所示。由表1的结果可知：堆芯Pin-by-pin SP3计算的计算精度普遍高于组件均匀化的堆芯粗网节块计算；除由于误差抵消导致计算精度提高的两群扩散计算外，堆芯Pin-by-pin扩散计算的计算精度都低于组件均匀化的堆芯粗网节块计算。因此，SP3方法是堆芯Pin-by-pin计算的必要条件；随着能群数的增加，堆芯Pin-by-pin简化球谐函数计算精度显著提高。七群SP3计算中特征值误差小于50pcm，最大棒功率相对误差低于2%，相对棒功率误差的AVG，MRS，MRE在1%以下；而在组件均匀化的粗网节块计算中，特征值误差为219pcm，最大棒功率相对误差接近10%。因此，七群是适用于堆芯Pin-by-pin计算精度的能群数目。

组件均匀化粗网节块计算的棒功率误差分布如图3所示，堆芯Pin-by-pin扩散计算和SP3计算的棒功率相对误差分布分别如图4和图5所示。可以发现，最大棒功率相对误差出现在组件与组件交界面以及燃料栅元与反射层交界面附近。这是堆芯内组件真实环境与单组件计算中全反射边界条件之间的不同所导致的。

3 结语

本文在压水堆堆芯Pin-by-pin计算中采用广义等效均匀化方法作为均匀化技术，对矩形指数函数展开扩散方法和SP3方法推导了零阶不连续因子和二阶不连续因子的计算公式，产生了适用于扩散计算和SP3计算的Pin-bypin等效均匀化参数。基于KAIST基准题，分析了压水堆堆芯Pin-by-pin计算中应用Pin-by-pin不连续因子的堆芯计算精度，与传统组件均匀化计算方法相比，应用了广义等效均匀化方法的压水堆堆芯Pin-by-pin计算的计算精度更高。7群简化球谐函数方法是高精度堆芯Pin-by-pin计算方案的实施策略，与KAIST基准题一步法计算结果相比，其特征值误差小于50pcm，最大棒功率相对误差小于2%，相对棒功率误差的AVG，MRS，MRE都在1%以下。