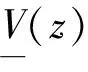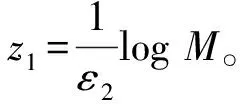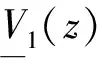一类Lotka-Volterra竞争模型中行波的最小波速选择机制

刘晓林,欧阳自根,郑肖肖

(南华大学 数理学院,湖南 衡阳 421001)

0 引 言

本文研究了下列非局部扩散的Lotka-Volterra 竞争模型[1]：

(1)

容易得到与之相关的动力系统为：

(2)

考虑系统(1)单稳的情况，假设竞争系数a1,a2满足下列不等式

a1<1

(3)

当条件(3)成立时，方程(1)有三个平衡点e0∶=(0,0),e1∶=(1,1),e2∶=(0,1)。引入一个新的变量z=x-ct，其中c为传播速度且满足c≥0，定义

(u,v)(t,x)=(U,V)(z)

是方程(1)连接e1到e0的一个解。因此U(z)和V(z)满足

(4)

受制于

(U,V)(-∞)=e1，(U,V)(+∞)=e0

(5)

S.Pan[2]证明了系统(1)的单稳态波的最小波速的存在问题，之后又被W.T.Li[3]推广应用到变换环境下的人口动力学模型中。通过J.Fang[1]以及X.Liang[4]在其文章中的论述，不难得知在系统(1)中存在一个临界值cmin≥0，当且仅当传播速度满足c≥cmin时，方程组(4)有一个非负的单调解。将其在e0处线性化得到

在生物学上，最小波速cmin表示入侵不稳定状态的物种的渐近传播速度，除非它等于c0，否则很难确定其公式[4-5]，这样可以给出最小波速选择机制的明确定义。

定义1若cmin=c0，则称最小波速是线性选择的；若cmin>c0，则称最小波速是非线性选择的。

随着最小波速问题被广泛研究，选择机制吸引了越来越多的学者的注意。在恒定系数的情况下，J.D.Murray[6]首先推测线速度c0是传播速度，但后来这一假设被Y.Hosono[7]否定并加以推进。本文旨在解决系统(1)的速度选择问题，将采用上下解方法和比较原理，来求解此类模型。

1 预备知识

本节给出了上下解的定义，并利用上下解方法证明方程组(4)行波解的存在性。

定义2若一对连续函数(U,V)(z)满足下列不等式

则称(U,V)(z)为方程组(4)的一组常规上解(下解)。

然而，一般情况下，很难找到一对这样的连续函数(U,V)(z)使其满足上述定义，所以给出较弱的非常规上下解定义。

根据S.X.Pan[8]论证的定理3.2，得到以下结论：

且不等式(3)成立，那么方程(4)存在一个正单调解(U,V)(z)使得

由上述引理得到行波解的存在性定理。

利用上述行波解存在性理论，将方程(4)线性化，连接e1到e0得到标量方程：

(6)

受阶数间隔[e2,e1]控制，定义

借助文献[9]中的引理3.3得知传播速度c*由下列(μ,c)系统唯一确定：

μ>0,f(μ,c)=0,∂μf(μ,c)=0。

令(μ*,c*)是上述方程的一个解，同时固定一个c1∈(c0,cmin)，易知存在一个μ1>0，使得f(μ1,c1)>0。定义

因为g(0,c1)=0且∂μg(0,c1)=0，可以得到μ2∈(0,μ1)使得g(μ2,c1)>0。

2 主要结论及证明

为了使计算简单化，采用文献[10]的思想，首先将证明对于任意给定的连续函数U(z)，满足U(-∞)=1和U(+∞)=0，使得满足V方程的解V(z)存在，且函数V(z)可以看作是V方程的上解或下解，所以我们提出下列引理。

引理2U(z)为给定的满足U方程条件的连续非增函数，且满足U(-∞)=1和U(+∞)=0，那么存在一个非增的函数V(z)使得下列方程成立

引理的证明，可参见文献[10]中的引理3.2。

根据上述引理，首先构U造出方程的上解，研究方程(4)的线性选择，得到了下面的结论。

定理2若条件

成立，则方程(4)的最小波速是线性选择的。

(7)

(8)

应用定理1建立线性速度选择机制，当c的值接近c0时，可以构造一个方程(4)的下解。定义一个连续函数

(1-a1)(1-Me-ε2z)+Ae-μ1z(1-Me-ε2z)(cμ1-

其中第一项中f(μ1,c)=0，第二项、第三项均为正，故

为了研究非线性速度选择，采用文献[10]中的引理3.8的思想，得到下述引理。

其中μ2在上节中已给出定义。那么当c∈[c0,c1)时，方程(4)不存在行波解。

定理3若条件

成立，则方程(4)的最小波速是非线性选择的。证明：首先构造一个下解，令

所以当

(9)