卡方检验在笔迹学中的应用
2020-07-16孙楠
孙 楠
(中国刑事警察学院,辽宁 沈阳110035)
1 概述
在文件检验中,尤其是笔迹检验,通常研究某种条件下是否导致某种现象的出现。如在改变温度的情况下,印章印文是否发生形变;在改变执笔位置时笔迹特征是否发生变化;在改变衬垫物软硬时笔迹特征是否发生变化等等,往往只根据发生变化的频数占总体样本的百分比来衡量某种现象出现的可能性,结果存在一定的偶然性和主观性。因此,利用卡方检验处理数据已经成为一种趋势。
卡方检验是一种非连续性资料的假设检验方法,所涉及的数据比较简单,计算过程也比较容易掌握,所以应用较为广泛。作为非参数检验的一种,卡方检验主要有三种用途,一是比较两个及两个以上样本率(构成比),即拟合度检验;二是两个分类变量之间有无关联性,即相关性分析;三是检验两个或两个以上总体的某一特性分布,也就是各“类别”的比例是否统一或相近,即统一性检验。对于进行相关性分析的这一用途来说,在卡方检验中,要判断两个变量是否具有相关性,不妨先假设这两个变量无相关性,进行理论上的分析,得到一系列理论值,然后以这些理论值为参照点,看实际值与理论值的绝对差距占理论值比例如何。从直观而言,如果两者很接近,在一定的条件下,就能认为两者没有差异,即两个变量彼此独立。[1]
2 应用
为研究戴手套书写笔迹特征的变化规律,设计如下实验:选取25名中国刑事警察学院的在校生,其中男性12名,女性13名。受试者在只改变书写方式即正常书写条件和戴普通薄手套书写条件下,对指定内容进行书写。分别制作笔迹特征比对表,充分比较同一人戴手套书写和正常书写形成笔迹之间的符合点和差异点,最后利用卡方检验对该实验的数据进行分析和总结,得到相应结论。
2.1 卡方检验公式推导验证
研究戴手套书写笔迹特征的变化规律,可以采用卡方检验从定性的角度说明某类笔迹特征的改变与戴手套书写这一条件改变是否具有相关性。本文选取运笔特征中的抖动弯曲现象来说明卡方检验公式的推导过程及实现过程。假设戴某一手套书写和正常书写出现抖动弯曲现象的人数如表1所示,其中变量是否出现抖动弯曲现象作为“行”,变量是否正常书写即正常书写或戴手套书写作为“列”。

表1 戴某一手套书写和正常书写出现抖动弯曲现象的人数
先假设H0成立:戴手套书写与出现抖动弯曲现象无相关性。用A表示正常书写,用B表示不出现抖动弯曲现象,则“戴手套书写和出现抖动弯曲现象没有关系”,等价于“戴手套书写和出现抖动弯曲现象独立”,即假设H0等价于P(AB)=P(A)P(B)。表1中的a恰好为事件AB发生的频数;a+b和a+c恰好为事件A和B发生的频数。因为频率近似于概率,所以在H0成立的条件下应该有即a≈(a+b)·,其中n=a+b+c+d。假设H0下,可以推得在(a+b)个正常书写的人中,不出现抖动弯曲现象的理论频数a理=(a+b)·。据概率论的基础知识,H0⇔P( AB)=P(A) P(B)可推导H0⇔P(B)=P()P(B)⇔P( A)=P(A) P()⇔P()P(),所以出现抖动弯曲现象的理论频数为b理=(a+b)·,在(c+d)个戴手套书写的人中,不出现抖动弯曲现象的理论频数c理=(c+d)·,出现抖动弯曲现象的理论频数d理=(c+d)·。如果假设H0成立,那么理论频数a理,b理,c理,d理与实际频数a,b,c,d差异不会很大,但对应差值可能是负值,也可能是正值,因此考虑使用对应差值的平方来表现实际频率和理想频率的差异,又考虑到对应差值大小是一个相对概念,因此可以考虑将对应差值平方和除以理论频数后再求和,即[2]这正是卡方检验中独立四格表资料检验的公式,说明此情况适用卡方检验进行验证。

2.2 实现过程
在自由度确定时,每一个X2值与一个概率值相对应,此概率即为在H0假设成立的前提下,出现一个这样或更大差别样本的概率。将上述表1中的数据依次代入该式子,得到卡方值X2=5.556。可以通过查看卡方对应P值表,获得P值为0.018(P<0.05),故拒绝H0假设;也能应用Excel提供的CHIDIST函数计算显著水平为0.05,自由度为(2-1)×(2-1)=1的卡方分布的P值,在Excel单元格中键入“=CHIDIST(5.556,1)”,按回车键,得到P值为0.018(P<0.05),拒绝原H0假设。最终,均得到戴手套书写与出现抖动弯曲现象有相关性的结论。对于此处卡方值的计算也可以使用SPSS统计软件实现,利用软件输入上述a、b、c、d对应数据,可得到概率P值,将P值与0.05进行比较,可得到两变量是否具有相关性的结论。此方法更简单快捷。SPSS软件操作过程和检验结果如图1~图4所示。[3]

图1 录入数据

图2 对数量(频数)进行加权
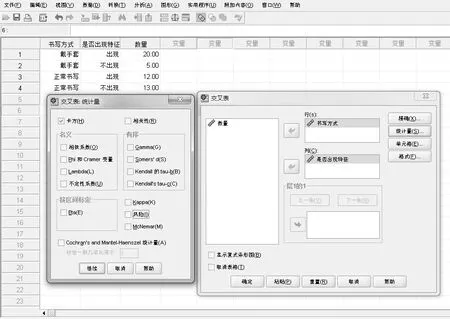
图3 进行卡方检验

图4 检验结果
图4 中的检验结果众多,不同条件P值不同,通常规定:(1)当两组总样本量n≥40且全部单元格的理论频数T≥5时,看第一行Pearson卡方的结果;当P≈检验水准时,看第四行Fisher的精确检验的结果;(2)当两组总样本量n≥40但有1≤理论频数T<5时,看第二行连续校正的结果,或看第四行Fisher的精确检验的结果;(3)当两组总样本量n<40,或最小理论频数T<1时,看第四行Fisher的精确检验的结果。本例中适用第一行Pearson卡方的结果P=0.018(P<0.05),同样拒绝原H0假设,也得到戴手套书写与出现抖动弯曲现象有相关性的结论。
3 总结与展望
目前只有极少数论文中使用卡方检验这一方法处理数据,讨论书写条件与笔迹特征变化的相关关系,讨论笔顺多样性与性别的相关关系。本论文通过公式计算法、Excel计算法、SPSS软件法对卡方检验在笔迹学中判断两变量是否具有相关性的应用做了简要介绍,为今后在笔迹学中应用卡方检验和更深层次研究其他统计方法投石问路。
将卡方检验运用到笔迹学中,对实验数据进行处理,能深入研究笔迹的影响因素,可以得到更科学、更详尽、更有说服力的结论。因此,笔迹学与卡方检验的结合是笔迹学从依靠主观意识进行模糊定性到依靠数据和统计方法进行精确定性的一大进步,这一方法具有很强的适用性和发展性,有待进一步推广使用。
