干线绿波协调控制优化研究
2020-07-16黄慧琼欧方前
黄慧琼,欧方前
(广西科技大学 机械与交通工程学院,广西 柳州 545006)
0 引言
快速增长的城市机动车辆给城市干道带来巨大的交通压力.现有的道路设施条件无法改善现有交通状况,只有通过提高交通管理与控制手段来解决.“绿波带”协调控制是最有效的方法之一.通过对干线上连续几个交叉口信号灯联动控制,使行驶的车辆每到达一个信号控制交叉口时正好遇上绿灯或少遇红灯,获得不停顿的通行权,形成连续交通流,可减少干道交通流的停车次数和延误时间,缓解城市交通拥堵状况[1].
目前,学术界对干线绿波协调控制的研究已较为成熟.国外这方面的研究较早,有着显著的成就.经典的研究以Little的MAXBAND模型[2]和Gartner的MULTIBAND模型[3]为主,这两个模型有一个共同的特点,就是都使用了混合整数线性规划算法,同时两种模型都是定时式信号控制算法,目标都是使上行和下行双向绿波带宽尽量达到最大化.
我国在干线协调控制方面的研究比较晚,但也取得了许多成果.于德新等[4]基于数学规划方法,对经典MAXBAND模型进行改进,提出绿波带干线协调信号控制优化方法.卢凯等[5]通过引入绿波带宽分配影响因子与带宽需求比例系数,构造了一种新的绿波协调控制模型性能指标函数通式.朱和等[6]通过引入启动清空时间,对MAXBAND模型进行了优化.卢顺达等[7]通过研究经典双向绿波相位差和相序中制约双向绿波带带宽的瓶颈交叉口相关因素,并对其进行优化.当前干线信号协调控制为基于车辆到达驱动的被动响应型控制,针对其特点与不足,龙科军等[8]提出一种车联网环境下干线信号协调控制与车辆速度主动引导的协同优化方法.李永强等[9]针对传统绿波协调控制的缺点,提出一种基于路网特性和交通需求数据驱动交通响应绿波协调信号的控制方法.曲大义等[10]考虑到交叉口间的关联性,提出了一种基于交通波理论的干线交叉口相位差协调优化模型.吕少姣等[11]以城市交通干道的延误时间最小化为研究目标,通过遗传算法和混沌优化算法在交通干道协调控制相位差优化上的应用,提出一种基于Logistic映射的混沌遗传优化算法.
上述成果对本文的研究奠定前期基础,但干线绿波协调控制可优化的方面还很多.本文主要是优化干线绿波定时协调控制主要参数中的共用周期和相位差,建立比较符合实际交通状况的线控协调模型,从而达到干线畅通有序的效果.
1 参数优化建模
1.1 共用周期优化建模
在绿波协调控制系统中,共用周期选取或大或小的值都会对各个交叉口的车流通行能力与车辆延误时间造成严重影响.在干线协调控制系统中,如果选取不是最大的那个周期时长作为公共周期,系统内将会有部分交叉口因周期过短而导致通行能力小于实际交通量,所以得选取最大的周期时长作为公共周期,对应的交叉口称为关键交叉口.当干线交叉口之间距离较远,相邻交叉口在同一时间内显示相反灯色的时候,各个相邻交叉口之间的距离满足:

式中:D——相邻交叉口间的距离,m;M——整数倍;V——线控制系统车辆通行速度,m/s;C——线控系统中的公用周期,s.
逆推可得理想共用周期Cm1:

综合考虑韦伯斯特以及考虑交叉口间距的理想共用周期,可得交叉口周期改进计算公式:
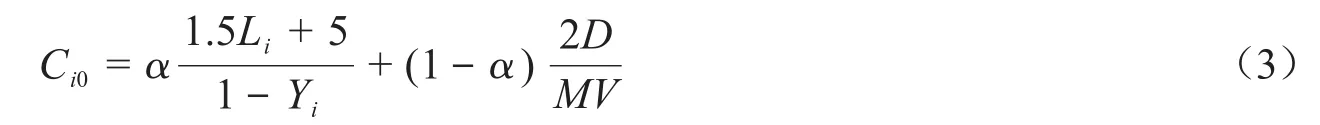
式中:Ci0——改进后的交叉口i信号周期,s;α——权重,α∈(0,1),根据实际情况取值;Li——在交叉口i一个周期内损失时间的总和,s;Yi——交叉口i组成周期的全部相位的最大流量比之和.
改进后的公共周期为Cm:

1.2 基于MAXBAND改进的相位差优化
1.2.1 动态红灯车辆排队模型
本线控制系统中各交叉口间的相位差计算以最大绿波带法为基础.由于交通规模的增大,次干道车流出入主干道,会影响原来求得的绿波带和相位差,因此,要考虑次干道车流出入主干道的影响,对MAXBAND模型进行改进.
在两相位车辆排队消散时间模型的基础上[12]进行四相位车队排队消散模型的研究,并且考虑了主干道车辆出入情况.以四相位的十字交叉口为例,其相位情况如图1所示.

图1 交叉口相位情况Fig.1 The Phase condition of an intersection
假设在此双向行驶道路上,南北为主干道方向,东西为次干道方向,南北方向为上行方向,北南为下行方向;道路有两个十字交叉口,上游交叉口用i-1表示,下游交叉口用i表示.以上行方向为例,上行方向的上游交叉口i-1驶向下游交叉口i的车流量有:相位1初期,南进口直行饱和流量和东进口右转平均流量,到相位1中后期变为南进口直行平均流量和东进口右转平均流量;相位2和相位3,东进口右转平均流量;相位4初期,西进口左转饱和流量和东进口右转平均流量,到相位4中后期变为东进口右转平均流量和西进口左转平均流量.则上游交叉口驶出车流量qu,i-1()t的表达式为:
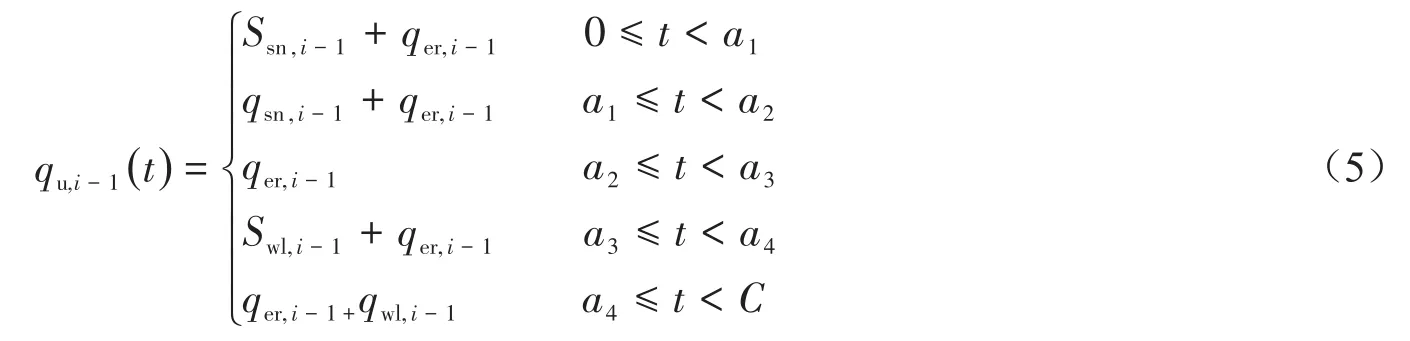
其中:
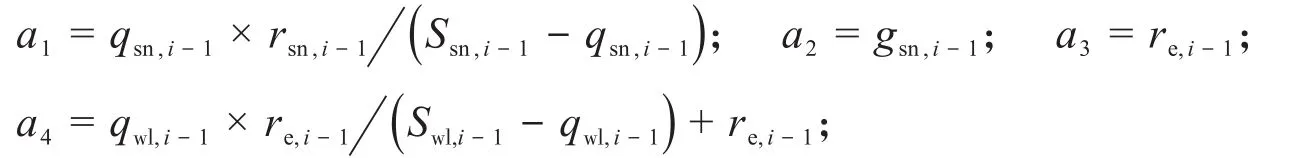
式中:Ssn,i-1——上游交叉口南进口直行饱和流量;qsn,i-1——上游交叉口南进口直行平均流量;Swl,i-1——上游交叉口西进口左转饱和流量;qwl,i-1——上游交叉口西进口左转平均流量;qer,i-1——上游交叉口东进口右转平均流量;gsn,i-1——上游交叉口直行方向绿灯时间;rsn,i-1——上游交叉口直行方向红灯时间;re,i-1——上游交叉口东进口方向红灯时间;C——信号周期,s.
从b时刻开始,上游交叉口驶向下游交叉口并且停在停车线后排队等待,直到d时刻车辆排队达到最大数量.用Pi()T表示,其表达式为:

由此可求得下游交叉口红灯期间的排队车辆数为:
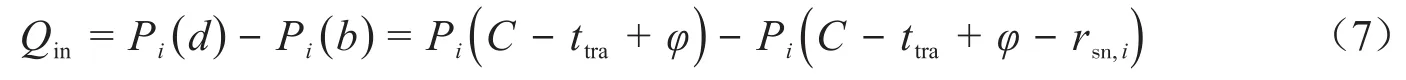
式中:ttra——两交叉口之间的行程时间,s;rsn,i——下游主干道的红灯时间,s;φ——上游交叉口与下游交叉口的相位差,s.
但在驶入下游交叉口的车辆数中并不是所有的车辆都是直行的,其中会有一部分车辆在到达下游交叉口南进口时右转或左转进入次干道.即qsnr,i×rsn,i辆车右转进入次干道,qsnl,i×rsn,i辆车左转进入次干道.其中qsnr,i为下游交叉口南进口右转平均流量,qsnl,i为下游交叉口左转平均流量.所以最终的红灯排队车辆数为:
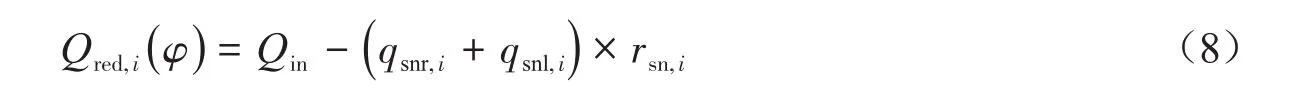
1.2.2 排队车辆消散时间模型
由于红灯期间的车辆排队,所以下次绿灯开始时刻,车辆排队开始消散,其消散时间计算公式为:

式中:τi(φ)——排队车辆消散时间,s;Ssn,i——干线直行方向饱和流量,pcu/h;tl,i——车辆启动损失时间,s.
1.2.3 MAXBAND改进模型
由于MAXBAND模型中的红灯车辆排队消散是固定的,用其作为参数所求的最大绿波带宽与实际的有较大的出入,从而使主干道方上的协调方向的车辆行驶到下一个路口时,既可能会遇到绿灯,也可能会遇到红灯.因此,将固定的红灯排队消散时间τi改为相对相位差的函数τi()φ,就可得到改进的线性规划模型:
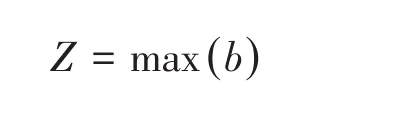
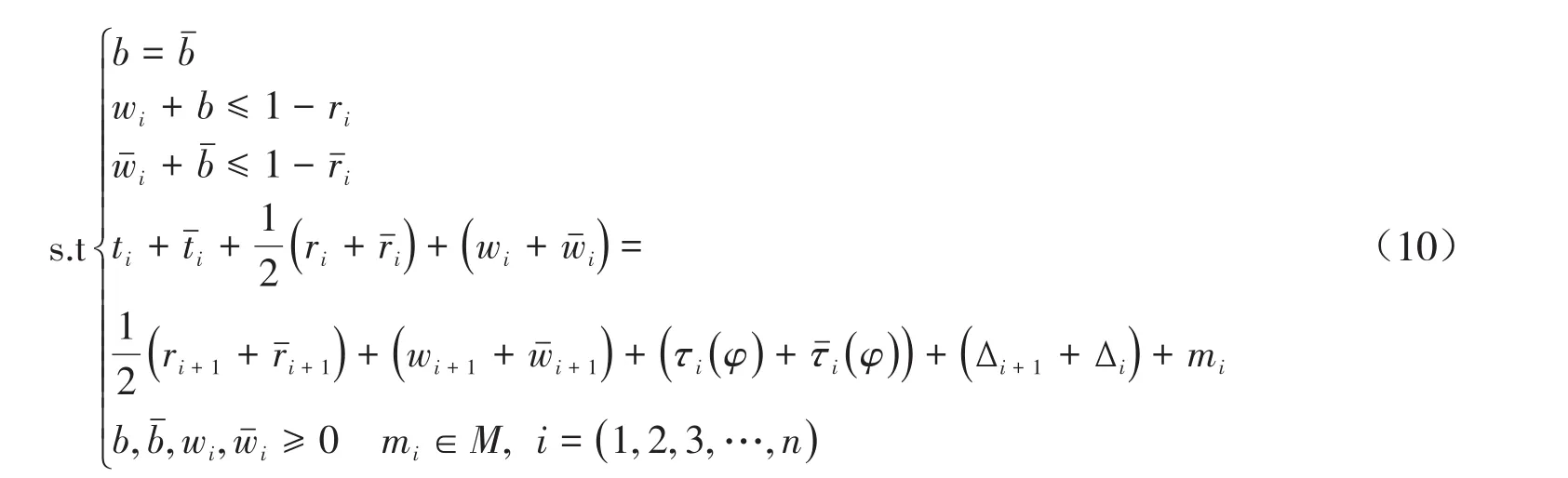
2 实例计算及仿真分析
2.1 基础数据情况
广西柳州市东环大道上南北依次为康顺路交叉口A、潭中东路交叉口B、高新一路交叉口C、高新三路交叉口D和高新五路交叉口E,选取B、C、D、E这4个交叉口为研究对象.康顺路交叉口A与潭中东路交叉口B之间的距离为500 m,潭中东路交叉口B与高新一路交叉口C间的距离为650 m,高新一路交叉口C与高新三路交叉口D间的距离为700 m,高新三路交叉口D与高新五路交叉口E间距离为670 m.经调查,4个交叉口各进口道高峰小时交通量如表1所示,各交叉口的相位信号配时方案如表2所示.
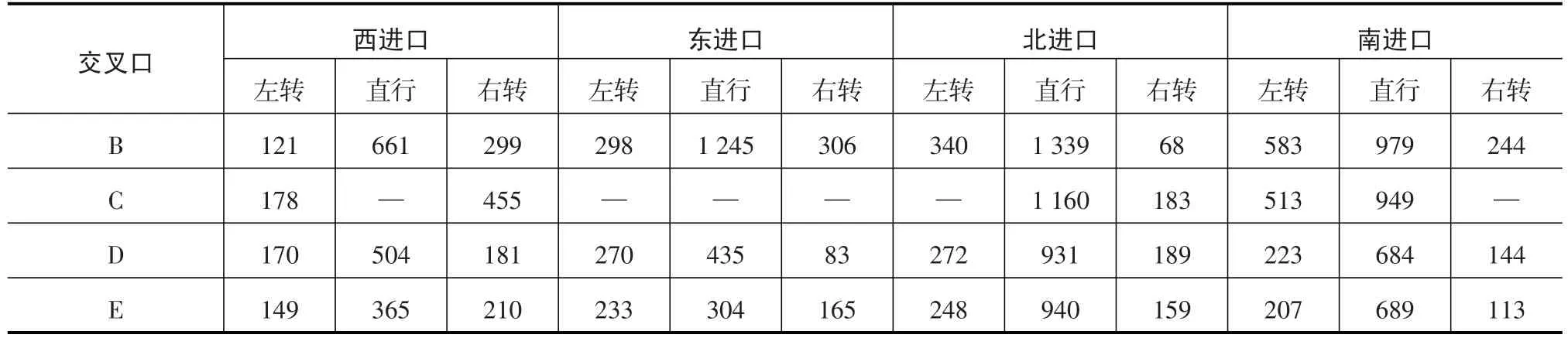
表1 各个交叉口高峰小时交通量Tab.1 Peak hour traffic at each intersection pcu/h
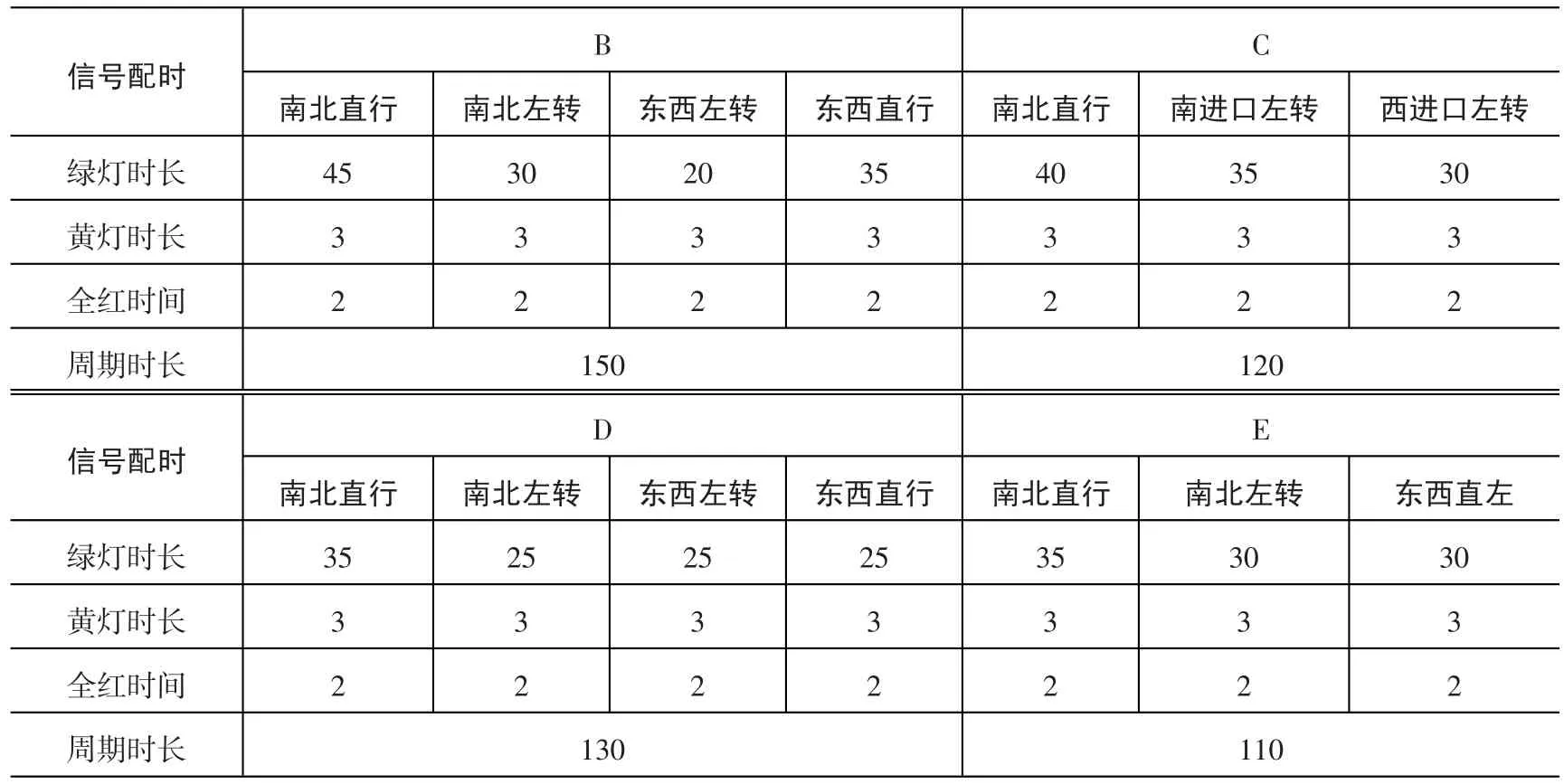
表2 各交叉口现有配时方案Tab.2 Existing timing scheme at each intersection s
2.2 信号控制参数计算
1)系统共用周期确定
东环大道上车辆的平均车速为13 m/s,根据东环大道上各交叉口进口道实际交通流量、相邻交叉口之间距离、交叉口渠化方式等,可计算得各个交叉口的设计饱和流量、总相位流量比和周期时长等参数.根据式(3)计算各交叉口信号周期,计算结果如表3所示.
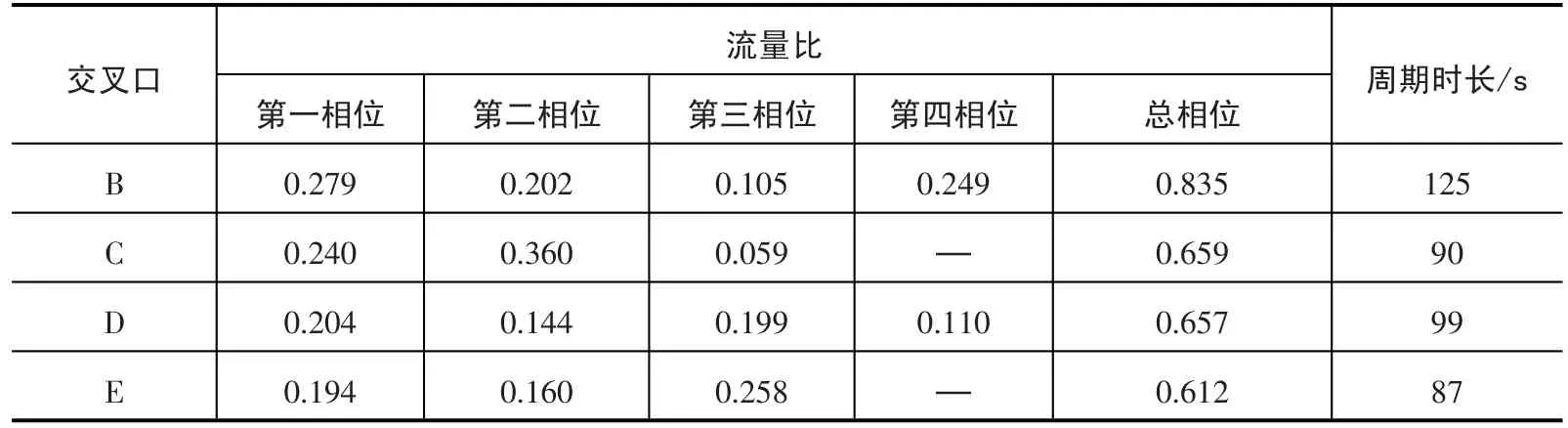
表3 各交叉口流量比及周期时长Tab.3 Flow ratio and cycle length of each intersection
根据式(4)可得系统的公共周期时长为125 s,对应的潭中东路交叉口B为关键交叉口.
2)绿信比确定
根据干线绿波控制系统共用周期计算各个交叉口的有效绿灯时间及绿信比,最终完成绿灯时间的分配.经计算,可得干线绿波协调控制系统最终配时方案,如表4所示.
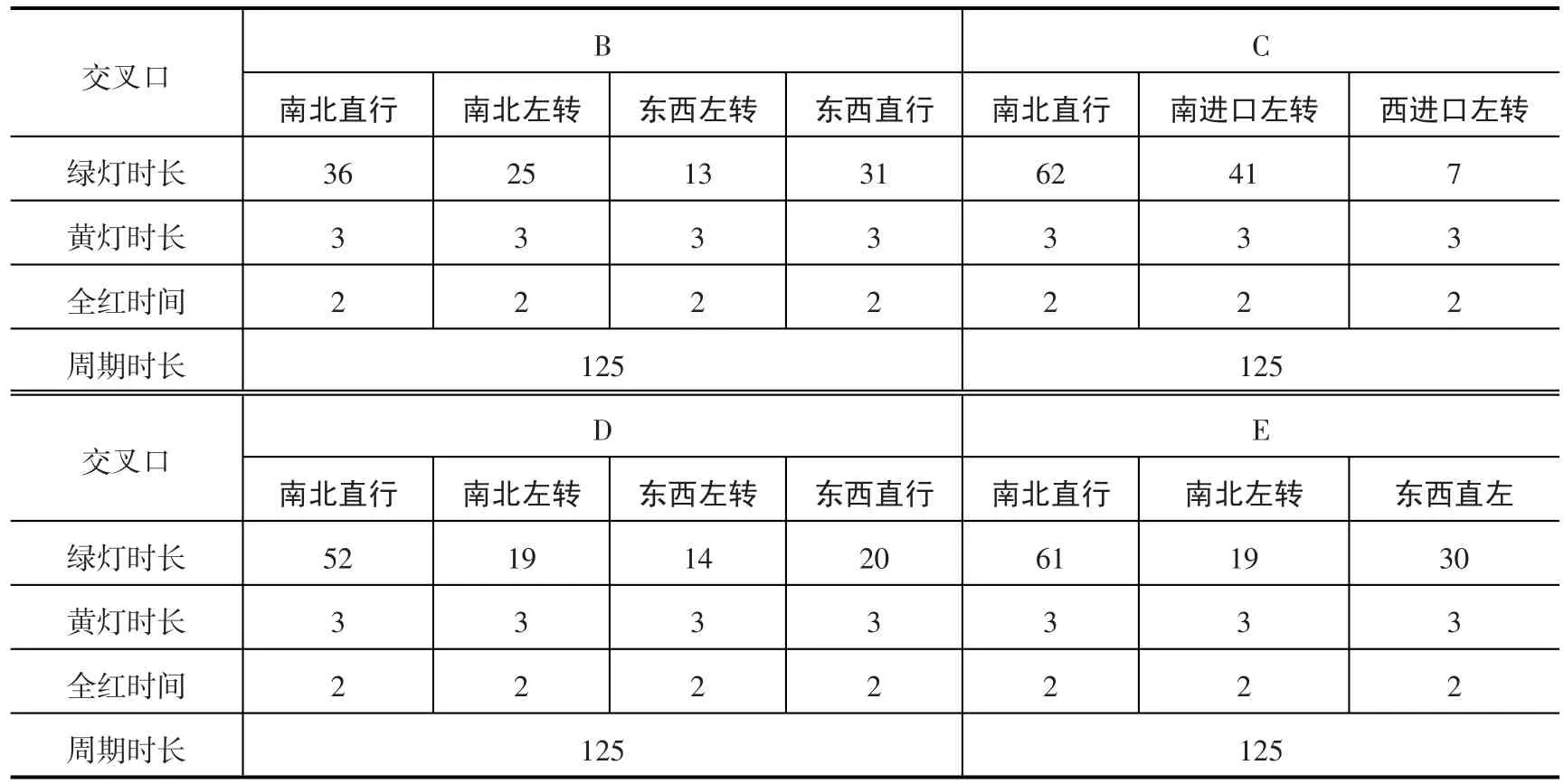
表4 交叉口各相位信号配时Tab.4 Timing of signal of each phase at the intersection
3)相位差确定
根据上文改进的最大绿波带法,潭中东路交叉口与高新一路交叉口的排队消散时间由式(5)—式(9)得:
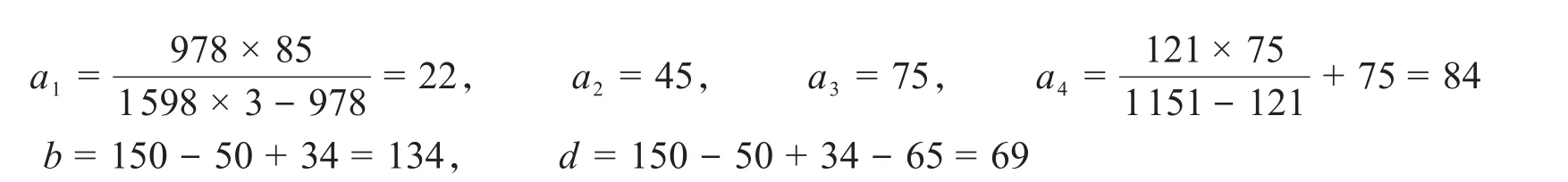
则可得从潭中东路交叉口驶向高新一路交叉口(上行方向)的车辆为:

由此易知在高新一路交叉口排队的车辆数为时间b与时间d所到达的车辆:
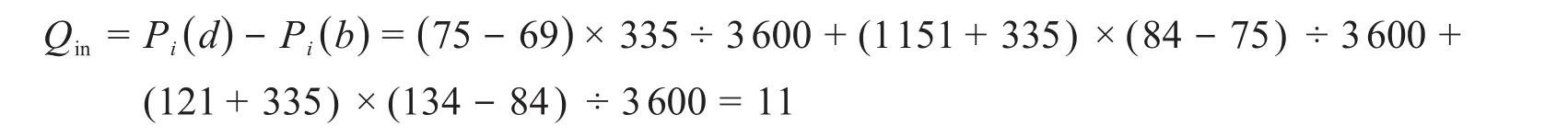
在高新一路交叉口南进口处有一部分车辆左转进入次干道(高新一路),则最终的红灯排队车辆为:
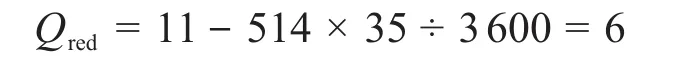
故高新一路交叉口C上行方向的红灯排队消散时间为:
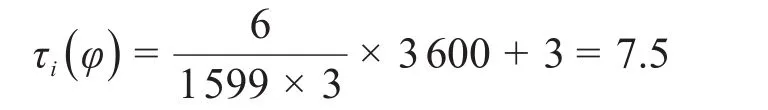
同理,计算下行红灯排队消散时间为13 s.
以此类推,可以求得上行方向中高新一路交叉口、高新三路交叉口和高新五路交叉口红灯排队消散时间分别为7.5 s、8 s、6 s,下行方向中高新三路交叉口、高新一路交叉口和潭中东路交叉口的红灯排队消散时间分别为9 s、10.5 s和13 s.
其他参数根据调查数据取值,如表5所示.上行wi、下行wˉi以及mi为所需要求的参数.
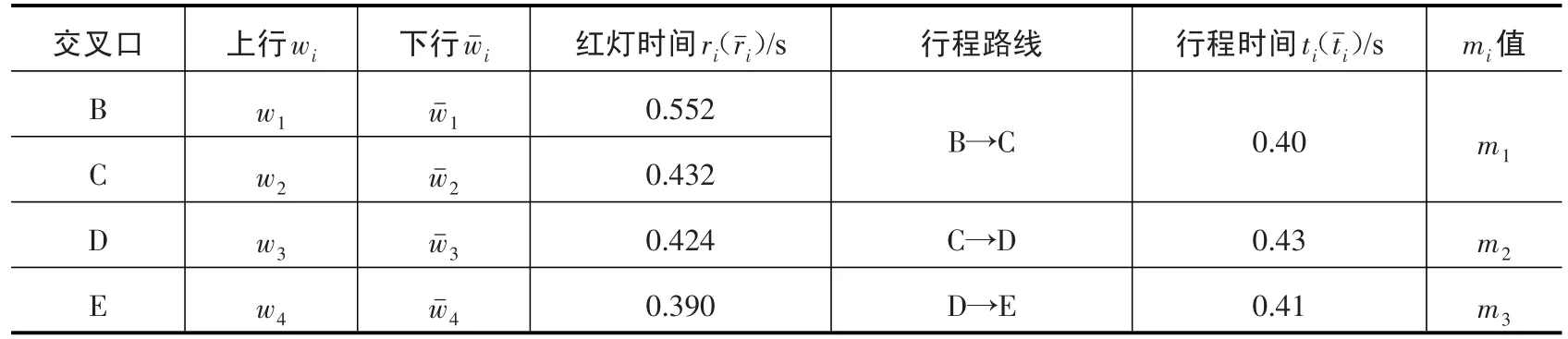
表5 最大绿波带模型参数取值表Tab.5 Parameter value table of maximum green wave band model
根据式(10),得到最大绿波带模型中的线性规划模型如下:

利用线性规划软件Lingo进行求解,求得b的最大值为0.22,表示占周期总时长的22%,最大“绿波带”的带宽为28s.
2.3 仿真分析
选择其中两个连续的交叉口用VISSIM软件进行仿真验证[13],选交叉口为高新一路交叉口C和高新三路交叉口D.采用对比法来比较优化效果,比较采用现有配时、相位差与采用优化后的配时方案、相位差的延误时间等性能指标,前者称为方案一,后者为方案二.将方案一、方案二进行仿真,再将仿真结果进行分析比较,如表6所示.

表6 方案一、方案二交叉口仿真结果对比Tab.6 Comparison of simulation results of intersection of scheme 1 and scheme 2
由表6可知:采用优化后配时方案和相位差,高新一路交叉口平均延误时长为15 s,平均排队车辆7辆,平均停车次数0.3次;高新三路交叉口平均延误时长为29 s,平均排队车辆9辆,平均停车次数0.6次;协调控制系统平均延误时长为31 s,平均排队车辆11辆,平均停车次数0.74次.方案二与方案一相比,高新一路交叉口平均延误时长减少了29%,排队车辆减少36%,停车次数减少了50%;高新三路交叉口的平均延误时长、排队车辆、停车次数与现在持平;协调控制系统延误时长减少了24%,停车次数减少了12%.
3 结语
通过对干线绿波协调控制中传统共用周期和相位差进行优化,结果表明:本次优化具有一定有效性和实用性.但本次优化过程中只考虑了两种影响因素,难免有所偏差,对于城市交通干线道路协调控制的优化研究,需要将更多影响因素考虑进去,方能将所设计协调控制系统更适用于实际交通状况的道路.
