挥舞旋转运动薄板磁弹性振动分析

冯小庭，王航，史骏

(西安铁路职业技术学院，陕西 西安 710026)

0 引言

在复杂物理场中的薄板振动分析可以指导很多实际问题。例如在热场、流场中做旋转运动的透平机械，其叶轮的振动可以简化为旋转运动薄板的振动。有大量的文献涉及导电物体的磁弹性振动分析，其中不乏作轴向运动薄板的磁弹性振动研究，亦有大量的学者研究了作旋转运动梁、板的振动分析。文献[1-9]分别对非线性振动特性、动力失稳特性、振动位移响板临界失稳荷载的影响做了深入研究，柔性薄板在磁场中的磁弹性振动分析已有丰富资料。作挥舞旋转运动的导电薄板的磁弹性分析尚不多见。导电材质的磁弹性分析有着现实的意义。

本文基于薄板理论，建立了旋转柔性薄板在横向磁场环境下的振动运动方程。应用Maxwell电磁定律得出导电薄板的电磁本构关系，使用Hamilton原理推导出在磁场中旋转运动薄板的动力学方程，并使用Galerkin法对方程进行离散，进一步研究挥舞旋转运动和磁场协同作用下薄板振动的特性。

1 系统建模

1.1 系统动能和势能

导电薄板在磁场中做旋转运动的模型，如图1所示。其中，惯性坐标系Oxyz，中心刚体的附体坐标系为O1x1y1z1，柔性薄板的附体坐标系为O2x2y2z2。x2轴、y2轴分别沿薄板的长、宽方向。中心刚体的半径为R，绕y1轴的转动惯量为J，板长为a，宽度为b，板厚为h。弹性模量为E，泊松比为μ，密度为ρ。薄板绕刚体中心轴线做旋转运动的角位移是θ。建立动力学方程时不计重力。

图1 系统模型示意图

薄板上任意一点P0(x,0,0)变形后的位置是P，其在浮动坐标系O2x2y2z2下的变形矢量为u=[u,v,w]T。在附体坐标系O2x2y2z2下的矢径为P点，在附体坐标系O1x1y1z1下的矢径为

r=(R+x+u)i+(y+v)j+(w)k

(1)

P点在惯性坐标系Oxyz下的矢径为

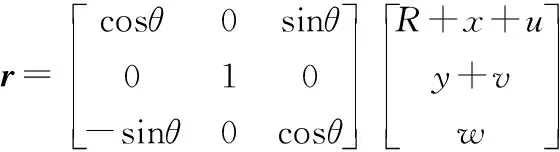
(2)

r关于时间求导，得P点的速度矢量

(3)

则系统的动能为

(4)

根据薄板理论，薄板横向变形引起轴向的缩短，得：

（4）建筑工程运维阶段应用。从全生命周期角度来看，建筑工程项目施工完成后，后期的日常运行和维护管理也至关重要。利用BIM技术能够根据建筑项目实际情况，同步获得建筑项目的使用数据，如项目容纳人员数、已使用时间、建筑财务等，以及承租人、租赁面积、收入分配、家具、设备库存等信息，根据相关信息的收集和运算，提升建筑物的经济价值，并通过相关成本运算，及时掌握建筑项目的短板和不足，提升用户体验。

(5)

计算系统势能时，忽略面内拉伸引起的变形以及中面变形，故系统势能仅是弯曲变形的应变能，即：

(6)

1.2 电磁力和电磁力矩

薄板内部的介质满足Maxwell电磁本构关系：

D=ε0E；B=μ0H；J=σ(E+V×B)；f=J×B

(7)

其中:V是旋转运动薄板各点的速度矢量;磁感应矢量为B(Bx,By,Bz)；电位移矢量为D(Ex,Ey,Ez)；电场强度矢量为E(Ex,Ey,Ez)；磁场强度矢量为H(Hx,Hy,Hz)；电流密度矢量为J(Jx,Jy,Jz)；ε0为真空介电常数；μ0为真空磁导率；σ为电导率；忽略扰动电场e。

设导电薄板在横向磁场中运动，即磁感应强度矢量为B(0,0,Bz)。此时单位面积所受电磁力和电磁力矩：

(8)

外力虚功为：

(9)

1.3 动力学方程

将式(4)、式(6)、式(9)代入式(10)。根据Hamilton变分原理

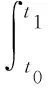
(10)

其中t0、t1为任意两个固定时刻。

(11)

2 振动分析

采用Galerkin法离散，设横向振动的解为

(12)

将式(12)带入变分方程式(11)中，由于广义坐标是相互独立的，故δqij的系数项分别为0。则振动方程整理为

(13)

其中广义坐标向量为：Q={q11,q12,…,q1N,…,qM1,qM2,…,qMN}T。将系统的振动方程整理为

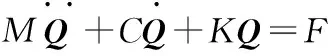
(14)

其中：广义质量矩阵

广义坐标一次导的系数矩阵

坐标的一次项系数矩阵

广义坐标的零次项系数矩阵

3 数值计算

磁感应强度为Bz=0.1T，薄板挥舞运动角速度Ω=10rad·s-1，时长为2s，薄板长为2m，宽2m，厚0.1m，中心刚体的半径R=0.2m，弹性模量为206GPa，泊松比为0.3，密度为7800kg·m-3，M=5,N=5。中心刚体运动角速度为

(15)

式中:Ω为稳态旋转角速度；T是旋转加速运动的时间，取为2s。

图2是在磁场中作挥舞运动的薄板不同阶振动模态。其中，图2(a)是m=1,n=1阶振动模态，相比于其他阶振动模态，其横向位移比较大，这说明(1,1)阶振动是实际振动的主要成分。

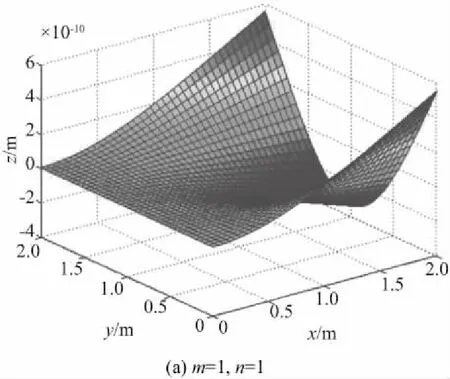
图2 1 s时振动模态

图3所示是不同时刻的横向变形位移图，可知作挥舞运动薄板在远离旋转中心的边缘处变形量最大，需要关注边缘处的疲劳强度。

当薄板绕y轴挥舞运动的角速度幅值不变且为20rad/s时，横向磁感应强度的取值依次为[0 T,0.1 T,0.2 T,0.3 T,0.4 T]时，x=a时的最大变形如图4所示。可知，发生最大变形时，边缘的变形曲线都是关于中心对称的，最大变形发生在坐标为(2,0)、(2,2)的角点处。不同的磁感应强度所对应的最大变形位移为[1.69×10-10,4.29×10-9,1.72×10-8,3.86×10-8,6.87×10-8]，单位为m。可知没有横行磁场时，变形量最小。随着磁感应强度增大，薄板的振动幅值变大。

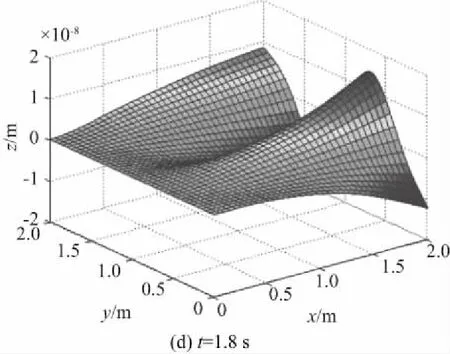
图3 不同时刻的横向变形位移

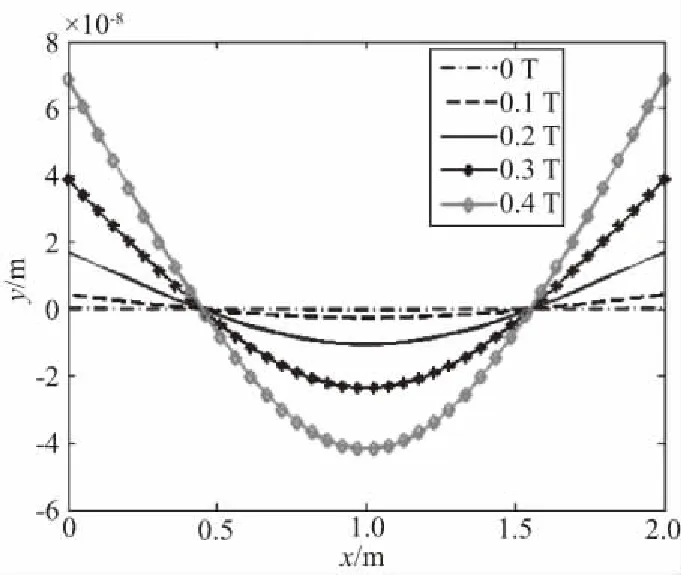
图4 x=a处的变形曲线(变形最大的时候)

当横向磁感应强度为定值0.1T时，薄板绕y轴挥舞运动的角速度幅值变化值取为[0,10,20,30,50]，单位为rad·s-1，不同的磁感应强度所对应的最大变形位移为[0,4.29×10-9,1.29×10-8,2.15×10-8]，单位是m。可知不旋转时，薄板没有变形。随着角速度增大，薄板的振动幅值变大(图5)。

图5 转速和最大变形量的关系

薄板的长宽之比变化时，角速度幅值为10rad/s时，横向磁感应强度取值0.1T，长宽比，即b/a=[0.1,0.2,0.5,0.7,1.0]。其最大变形如图6所示。不同的长宽比所对应的最大变形位移为[3.28×10-13,5.28×10-12,2.18×10-10,8.95×10-10,4.29×10-9]，单位是m。可知，随着长宽比增大，薄板的最大振动幅值变大。

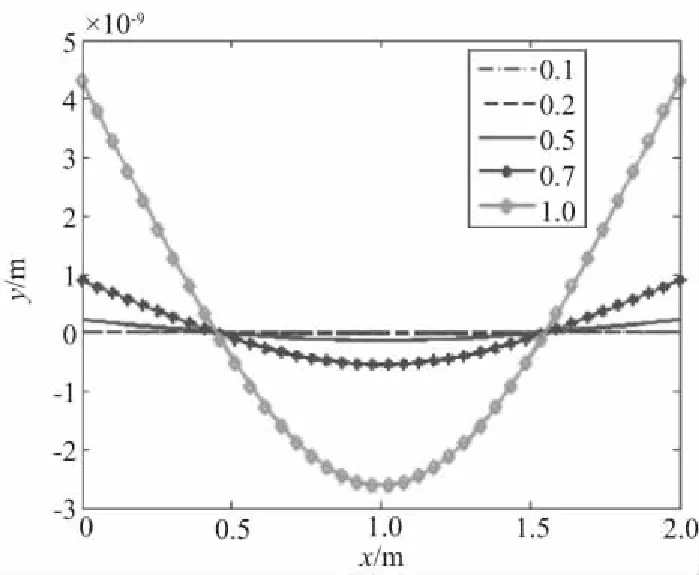
图6 板长和最大变形量的关系

4 结语

利用Hamilton变分原理，建立了在磁场中运动的薄板系统动力学方程。研究了该系统的振动特性。经过分析，得出如下结论:1) 推导了横向磁场中旋转运动薄板的非线性磁弹性振动方程。2) 薄板的振动以1阶振动为主。3) 薄板的振动幅值随着外界横向磁感应强度的增大而增大，随着旋转运动角速度的增大而增大，随着长宽比的增大而增大。4) 本文建立动力学方程的过程，可应用于其他在磁场中作旋转运动的厚板、层合板等。