基于PCE法的某涡轮泵转子动力学特性不确定性分析

沙粒子，王晓伟，穆鹏刚

(1. 南京航空航天大学 能源与动力学院，江苏 南京 210016； 2. 液体火箭发动机技术国防科技重点实验室，陕西 西安 710100)

0 引言

涡轮泵是火箭发动机的心脏，转子系统是涡轮泵的重要核心部件，其运行的稳定性及可靠性直接关系到涡轮泵的寿命。转子是旋转机械振动的主要来源，如何减少转子振动是设计制造旋转机械的重要课题[1]。

研究转子的动力学问题，首先需要对转子进行有限元建模。有限元建模需要足够的精度保证建立模型的准确性。除了确保模型的精度以外，还需要考虑计算效率。如果一个模型占用的空间过大，将会严重降低其计算效率。因此，平衡精度与效率问题就成了有限元建模的难点所在。蔡力钢等[2]研究了多种约束的机械式主轴有限元建模，发现把主轴考虑为用梁单元结果更为精确。边杰等[3]研究了当一种发动机转子没有具体样机时可用超模型去替代实物模型的有限元建模方法。

因为转子本身的构造复杂多变，加工难度高，会产生一系列不确定性的因素，如材料属性、加工尺寸、测量误差等。对于转子这样的高精尖部件来说，很小的误差可能会产生巨大的影响。因此研究转子的不确定性问题是很有必要的。白长青等[4]将不确定因素表示为一维随机场函数，给出了转子系统的随机响应分析方法。不确定性问题的研究方法有很多，其中多项式混沌展开法(polynomial chaos expansion, PCE)凭借其坚实的数学基础和良好的性能，近年来受到越来越多的关注，在数学及工业领域的应用也越来越广泛。本文将此方法应用到所建立好的转子模型上，验证了此方法的有效性，并指出不确定性对转子系统产生的重要影响。

1 基于PCE的转子动力学建模理论

多项式混沌理论总的来说就是用一系列与输入参数分布类型对应的正交多项式之和来近似精确地表示一个随机扩展的过程。最开始的多项式混沌是由WIENER[5-6]提出的，如式(1)所示。它是利用Hermite多项式来构建模型的。

(1)

式中：α(α0,αi1,…)是需要求解的多项式系数；ξ(ξi1,ξi2,…)是服从标准正态分布的随机变量。ξ=[ξi1,ξi2,…]的维数通常与原任意正态空间下的随机输入变量X=[X1,X2,…]的维数保持一致并存在一一对应关系。Hn(ξi1,…,ξin)是阶数为n的Hermite正交多项式。

对于转子系统，主要由转轴、作用在上面的圆盘和支承系统组成。根据M. I. Friswell等人[7]所著内容，其中转轴可以看成由不同分段的铁摩辛柯梁单元组成，每个节点有4个自由度。对于有直径变化、集中质量、连接方式改变等情况，则需要在该处进行分段。

将转轴、盘、支承等全部结合起来组成整体转子系统的动力学方程。其形式如下：

(2)

其中：M、G分别代表转轴和盘的质量矩阵、陀螺矩阵；K、C分别代表转轴的刚度矩阵和阻尼矩阵；Kb代表支承的刚度矩阵；q是整个转子系统上受到的激励项。

将方程转换到频域系统，得到下式：

Z(ω)X(ω)=Q(ω)

(3)

其中：

Z(ω)=-ω2M+iω(C+ωG)+K+Kb

(4)

转子动力学方程与其他系统动力学方程最大的区别就是它多了陀螺力项，因此会使系统的振动形式复杂更甚。接下来针对具体的转子系统进行不确定性建模分析。

2 某涡轮泵转子模型

转子的几何构造如图1所示，由转轴、诱导轮、离心轮、叶轮及大轮盘等构成。图示也给出了坐标方向，轴向为x向，径向为y、z向。

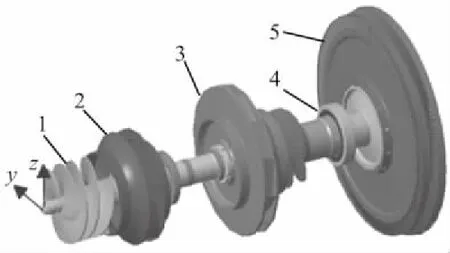
1—诱导轮；2—离心轮；3—中间轮；4—轴承；5—叶轮。图1 转子结构图

转子为套装转子，除轮盘采用螺栓紧紧与转轴相连以外，其他轮件均为单独部件，用槽约束其周向位移，轴向与套筒、挡圈等压紧。

3 基于试验数据的有限元模型修正

由于有实物样机，能够得到可靠的实验结果，所以在对转子进行动力学建模的过程中，可以不用建立超模型作为参考，直接建立简化模型，结果若偏差过大可以进行模型修正，使之与实验结果相匹配。

一般对转子进行有限元简化建模，可以考虑将转子分为若干段，在外接轮盘质心处、轴承安装处及转轴径向结构有较大变动处等部位截断,然后考虑实际的几何结构关系，考察各部件与转轴之间的物理关系。对于该转子，各轮部件都是套在转轴上，对转轴的刚性影响很小，故只需考虑它们在节点处的质量和转动惯量，而忽略其刚性的影响。转轴总共有16个节点，被分为15段。各段轴单元的质量、转动惯量与长度均与原有模型保持一致，其杨氏模量则可按照刚度等效的原则计算得到。

对有限元模型进行计算分析，对比初始杨氏模量下有限元模型前2阶固有频率计算结果与实验结果。在此基础上以实验结果为基准进行模型修正，得到修正后的杨氏模量。表1给出了修正后前2阶固有频率误差。

表1 修正后固有频率误差

由表1可以看出，修正后模型的固有频率十分接近实验值，说明该转子有限元模型可以代替实验模型。接着对修正后的转子有限元模型进行不确定性建模分析。

4 转子动力学特性的不确定性分析

对于此涡轮泵转子系统来说，中间部分是由大量轴环套装在一起的，对其施加预紧力以压紧。不同的预紧力会使中间轴环部分对该段转轴的刚性造成不同程度的影响，由此会带来实际建模过程中的不确定性问题。对此，针对其中环套2和环套3影响下转轴的杨氏模量的不确定性，基于PCE法对该转子系统进行不确定性分析。

环套2、环套3二者综合影响下的杨氏模量服从正态分布且波动值均为20%。采取1000个样本抽样得到的转子动力学不确定性频响曲线结果如图2-图4所示。图中中间由红蓝两条线组成，红色线代表确定值情况下的结果，蓝色线代表PCE法抽样结果的均值。两条绿色线则是多项式混沌展开法抽样计算得到响应的最大值与最小值曲线(因本刊为黑白印刷，如有疑问请咨询作者)。

从图2-图4中可以看出，由预紧力引发的转轴中间部分刚度的不确定性会引起整个转子系统的不确定。两个环套对转子系统的第1阶临界转速的影响很小，对第2阶临界转速的影响则相对较大。受两个环套综合影响的不确定性会呈现出比受单一环套影响更大的波动。

图2 涡轮泵转子不确定性频响曲线(环套2)

图3 涡轮泵转子不确定性频响曲线(环套3)

图4 涡轮泵转子不确定性频响曲线(环套2和环套3)

实际情况中受到影响的转轴刚度不确定性会更多，这种累加效应引发的不确定性的扩展会更大，由此会带来转子设计过程中的一系列问题。因此在涡轮泵转子动力学实验的过程中，应当考虑中间环套的预紧力。

接着考虑环套2和环套3综合影响下的转轴轴段杨氏模量波动值分别为10%和30%的情况。由于主要波动发生在第2阶临界转速附近，因此统计其附近的不确定影响,包括第2阶临界转速的转速范围和幅值范围。经计算，第2阶临界转速和幅值的准确值分别为625.1r/s、2.621×10-4mm。

由图5可以看出，转速的变化范围随着波动值的增加基本呈线性增加，而幅值的变化范围则呈现非线性。随着波动的加大，幅值变化的不确定性程度会更显著。

5 结语

论文针对火箭发动机涡轮泵转子系统的结构特点，以涡轮泵转子中的局部连接结构为研究对象，建立了转子系统的有限元模型，通过与模态试验结果对比及模型修正，前2阶模态的频率误差不超过4%。首先保证了有限元模型的准确性，其次将多项式混沌展开法应用到局部连接刚度含不确定性参数的动力特性建模及计算。通过结果分析可以发现，采用PCE法计算得到的含不确定性参数的转子前两阶临界转速均值十分靠近基准解，这证明了多项式混沌展开法的正确性。通过结果波动值的变化又可以看出连接刚度的不确定性在转子系统中呈现不同程度的扩展，这也就说明了涡轮泵转子中间轴环部分预紧力大小引发连接刚度的不确定性问题会对转子系统产生不可忽视的影响。

图5 波动大小对第2阶临界转速的影响