铣削机器人动力学建模及仿真研究
2020-07-16张永贵牛蓉周明夏恩帅
张永贵,牛蓉,周明,夏恩帅
(1. 兰州理工大学 机电工程学院,甘肃 兰州 730050; 2. 兰州空间技术物理研究所 真空技术与物理重点实验室,甘肃 兰州 730000)
0 引言
铣削机器人动力学建模和分析,对于其运动学分析具有重要意义。其主要有Lagrange法[1]、Newton-Euler递推法、达朗贝尔-虚功原理[2]等。Lagrange法不易求解复杂结构拉格朗日因子;Newton-Euler涉及到微分方程,推导过程复杂[3];而达朗贝尔-虚功原理,对于较复杂机构较为抽象[4]。
动力学仿真分析在机器人研究中起着至关重要的作用,也因此吸引了众多学者的研究。李辉等人[5]基于MATLAB对工业机器人在复杂工作路径下的动力学仿真进行研究。王战中等人[6]基于ADAMS和MATLAB对6臂机器人进行联合仿真,找出控制系统的不足之处并进行优化。马如奇等人[7]使用MATLAB/Simulink模块搭建其控制系统,基于ADAMS和MATLAB进行了联合仿真。文献[6-7]都是基于机器人三维模型导入ADAMS环境进行仿真分析,然后利用MATLAB/Simulink模块进行控制系统仿真,并不是对机器人动力学方程进行编程计算,没有验证动力学建模正确性的环节。
本文基于机器人在铣削过程中动力学状况对铣削加工质量的影响研究需要,以MOTOMAN UP50机器人(以下简称机器人)为对象,首先基于Creo软件对机器人三维虚拟实体模型进行建模,获得动力学建模所需的惯性参数;然后基于Newton-Euler递推法对该机器人建立动力学方程,并采用MATLAB软件对该方程进行编程,得到机器人末端执行器位移以及关节驱动力矩随时间的变化曲线;最后基于ADAMS对建立的三维模型进行虚拟样机动力学仿真分析,同样得到上述的变化曲线,通过对比验证了所建机器人动力学模型和所编制计算程序的正确性,为后续研究奠定了基础。
1 动力学模型的建立
1.1 三维模型的建立
图1为基于Creo软件建立的机器人虚拟样机。在 Creo “质量属性”工具中测得机器人各关节的质量mi,质心位置rci及惯性矩阵Ji,如表1所示,为后续基于MATLAB对机器人的动力学编程提供数据。

图1 MOTOMAN UP50机器人三维模型

表1 机器人各关节惯性参数
为方便对该机器人进行动力学研究,对图1所示的机器人建立如图2所示的坐标系,该坐标系采用改进D-H法[8]建立,然后依据此图可建立动力学方程。
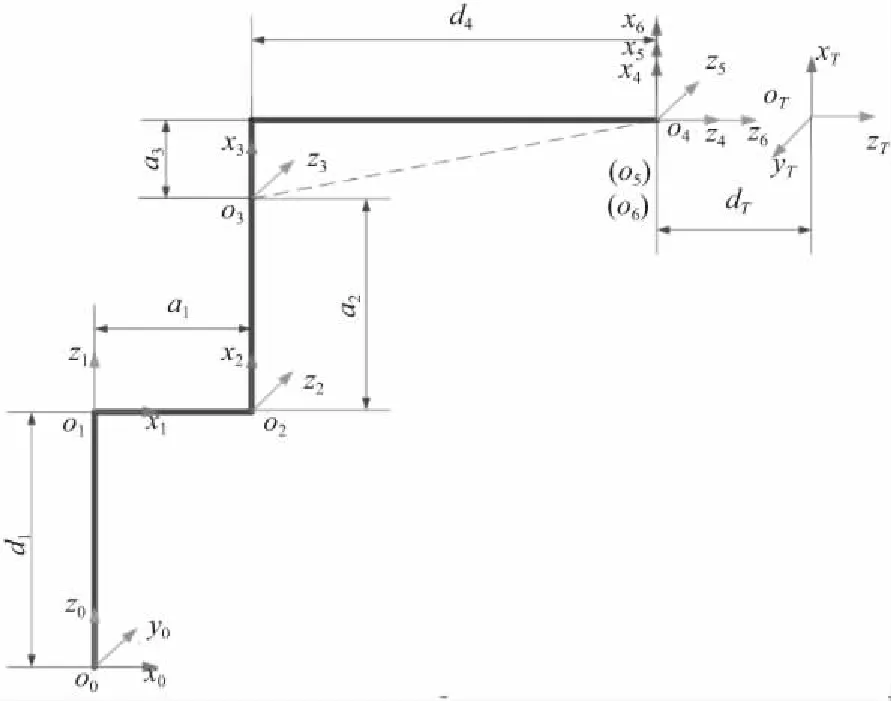
图2 铣削机器人连杆坐标系
1.2 动力学建模
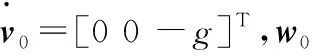
(1)
式中i=0,1,2,3,4,5。
公式(2)解决了各关节的相互作用力、力矩、关节驱动:
(2)
式中:i=6,5,4,3,2,1;
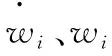
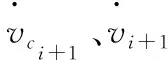
Zi表示指定杆件坐标系的每个Zi轴向单位向量;
Zi+1表示指定杆件坐标系的每个Zi+1轴向单位向量;i+1表示第i+1根杆件;

Ri+1表示杆系{i+1}的旋转矩阵;

Pci+1表示坐标系统中的位置矢量{i+1 };

Ici+1表示i+1杆相对于质心的惯性张量;
Ni+1、Fi+1分别表示i+1杆件惯性力矩以及质心处惯性力;
ni、fi分别表示i关节上的平衡力矩以及平衡力;
τi表示i关节中的驱动力矩。
1.3 求解关节力矩
当机器人工作时,已知其工作路径,而且在各关节变量均为固定值的条件下,依据式(1)-式(2),可按顺序推出各关节添加的驱动力。在已知各连杆速度、加速度和惯性张量的情况下,通过Newton-Euler方程,可以反推机器人铣削过程中末端的铣削力,得到各关节的作用力,为实现ADAMS动力学仿真提供理论依据。
基于表1利用连杆坐标系计算每个臂杆的姿态矩阵和位置矢量,然后基于第1节Newton-Euler法在MATLAB中编写逆动力学算法程序,设置铣削加工所需要的轨迹,按照其轨迹编写驱动函数,对1.2节动力学模型进行理论计算,得到角位移和各关节驱动力矩。
该机器人的初始位置为q0=[0 -90 0 0 0 0]T。根据铣削加工机器人工作需要,可规划该机器人在MATLAB的末端轨迹,其运动路径如图3所示。图4显示了在该路径下,通过程序计算出的6个关节驱动力矩随时间变化的曲线。
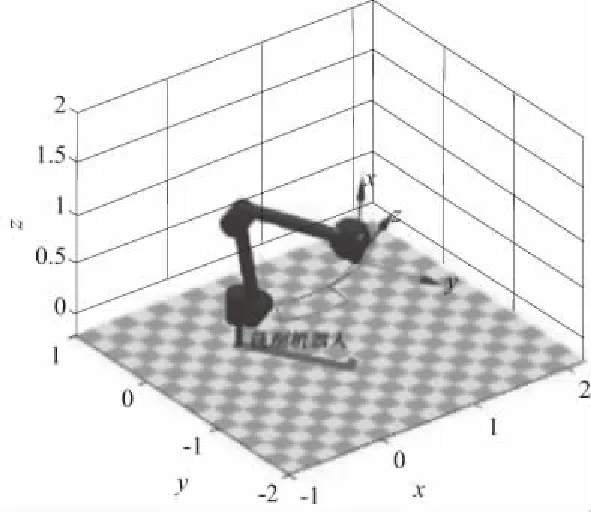
图3 MATLAB中铣削加工运动轨迹
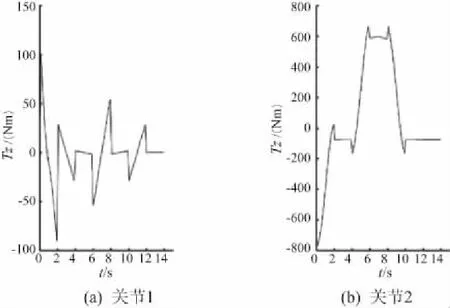
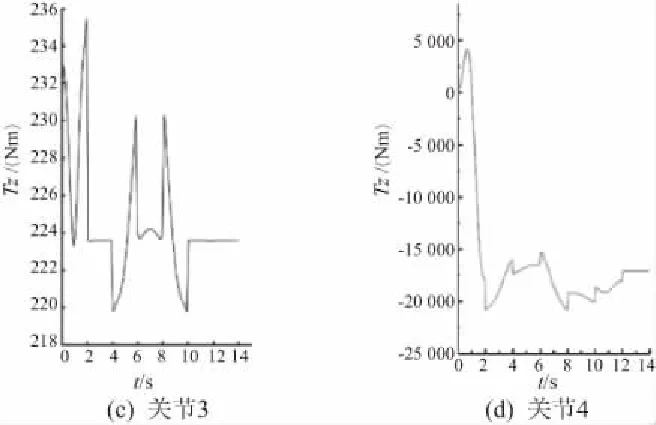

图4 MATLAB中计算的各关节力矩曲线
2 ADAMS动力学仿真验证
使用Creo来简化机器人的三维模型,接着导入ADAMS以建立虚拟样机模型,设置对应的材料特性、约束、驱动函数和外力等动态参数,最后进行动力学仿真。
2.1 添加驱动函数
将MATLAB中的驱动,运用“save q.txt -ascii a”指令将其导出并保存为txt格式,然后将其导入到ADAMS中生成样条曲线,最后在各个驱动上添加相应的驱动函数。腰关节、肩关节、肘关节、手腕旋转关节、手腕摆动关节、手腕回转关节的驱动函数都表示为:
CUBSPL(time,0,SPLINE_1,0)。
2.2 添加末端铣削力
当铣削条件、铣削用量以及铣削材料等各要素条件都选定时,即根据铣削加工要求选择工件材料为可锻铸铁,刀具材料为铝合金,直径为6mm的圆柱铣刀,且电主轴转速为3000r/min。根据刀具材料和铣削工件材料选择铣削公式进行计算主切削力,计算公式如下:
(3)
其中:FZ为铣削力,N;CFZ为铣削力系数,铝合金的CFZ可取钢的1/4(钢的CFZ为641);ae为铣削宽度,mm,(圆柱铣的ae=0.05d0);af为每齿进给量,mm(圆柱铣的af为0.1~0.2);z为铣刀的齿数;d0为铣刀直径;KFZ为铣刀铣削力修正系数,当刀具的前角系数为0时,KFZ=0.89。
其中ns为主轴转速。一般铣削进给速度的计算公式为:Vf=f×ns=af×z×ns(mm/min)。
当圆柱铣刀的每齿进给量取0.1mm,铣削深度取0.2mm时,可以计算出末端铣削力FZ为388N。
添加铣削力后,将模拟结束时间设定为14s,将其模拟步数设定为500,并使用ADAMS/PostPocessor后处理模块分析机器人,可得到该机器人在ADAMS中的运动轨迹如图5所示,可输出该铣削机器人末端执行器位移和各关节驱动力矩。

图5 ADAMS中铣削加工运动轨迹
3 动力学曲线拟合分析
通过MATLAB计算和ADAMS仿真分析得到该机器人末端执行器位移和各关节驱动力矩。机器人末端执行器位移变化情况对比结果如图6所示(因本刊为黑白印刷,如有疑问请咨询作者)。

图6 末端执行器位移对比曲线
由图6可知,机器人结束时产生的运动轨迹基本上与期望的运动轨迹相同,只有在1.8s之前有轻微的偏差,因此z方向的误差最大值是0.80%,而x方向和y方向的误差值最大值分别是0.92%和0.86%。通过图6可以看到,机器人末端执行器位移在MATLAB和ADAMS环境下的曲线基本吻合,充分证明机器人系统运动相对稳定,可以验证所建立的机器人动力学模型的有效性。
图7为机器人各关节驱动力矩随时间变化情况的对比分析,其中计算结果指在MATLAB中进行编程计算得到的数据,仿真结果指在ADAMS中进行仿真分析得到的数据。
比较图7可以看出,各个关节力矩的仿真和计算曲线的趋势基本一致,且较大误差均出现在曲线的波峰、波谷处,关节力矩曲线对比图的最大误差分别为0.250Nm、0.001Nm、0.200Nm、0.001Nm、0.010Nm、0.120Nm,两者都在所允许的误差范围之内。误差产生的主要原因是ADAMS环境中的动力学仿真更加接近工程环境,在仿真时如出现较大波动,ADAMS能够更好地处理机械构件惯性影响,较编程计算更加准确,从而可验证所建立的机器人动力学模型的合理性。
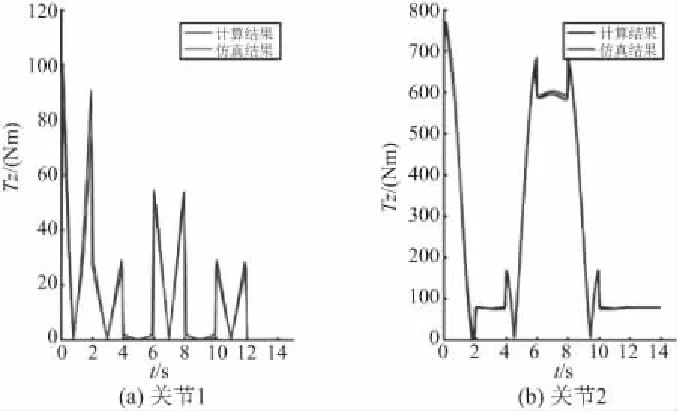

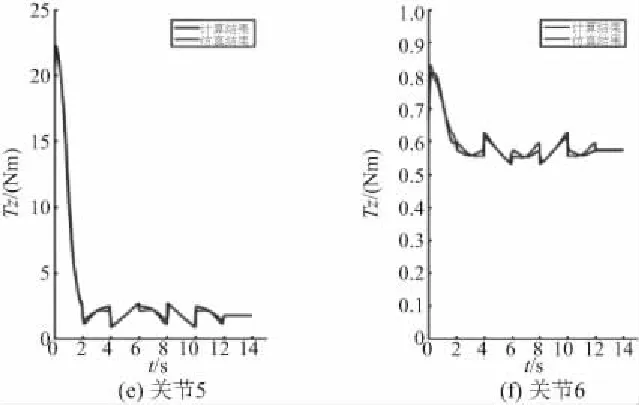
图7 各关节MATLAB计算和ADAMS仿真力矩拟合曲线
4 结语
1) 基于Creo三维软件建立机器人三维虚拟实体模型,获得动力学建模所需的惯性参数;基于Newton-Euler方程建立机器人的动力学模型并在MATLAB环境下编程计算,可以对6自由度铣削机器人进行动力学研究分析。
2) 对于同一机器人,在设置了同样的铣削加工路径的情况下,基于Newton-Euler方程进行MATLAB编程计算的结果与基于ADAMS仿真分析的结果基本一致,可以验证基于Newton-Euler递推法所建立的铣削机器人在铣削规定路径时动力学模型的正确性。
