B样条曲面光滑拼接方法

2020-07-16黄吴戟王志国

机械制造与自动化 2020年3期

黄吴戟，王志国

(南京航空航天大学机电学院，江苏南京210016)

0 引言

飞机、船舶、车辆的外形非常复杂，需要由大量曲面片拼接而成。无论是从美学设计角度考虑，还是从满足流体力学性能以减小阻力的角度来说，这些产品的外形数模往往由大量曲面碎片光滑拼接而成。从产品的初步模型直至得到最终模型的过程中，往往伴随着设计人员大量的时间与精力的投入，以期产品模型满足相关设计需求。可见，高效实用的曲面变形方法对设计过程的效率提升是不言而喻的，更能从中获得可观的经济效益。而这些产品模型的曲面变形设计方法是产品设计过程不可缺少的一项技术。

20世纪80年代，BARR[1]率先对曲面的变形以几何的形式做出描述，随后，WATT A[2]等学者对BARR的变形手段做出了进一步完善与发展。1986年，学者SEDERBERG T W[3]给出了一种著名的自由变形方法，即FFD技术。王小平等提出了一种基于多项式幂基因子的参数曲线曲面变形手段[4]，该变形手段计算量不大，且不被几何描述局限，其核心思想是通过仿射变换矩阵作用于曲线曲面的参数方程上，非常简明，但变换后的几何形状无法用STEP标准表达，因此适用范围不广。于超升[5]通过刚架模型利用有限元方法实现曲面变形，该方法避免了几何约束方程的建立，对于曲面拼接有实用性。崔洺瑞[6]等利用曲率信息延拓曲面实现了对曲面上孔洞的填补。目前，国内外曲面变形研究的成果主要集中在对单张曲面进行变形与调整的效果上。然而用单张参数曲面去表达复杂的产品外形过于勉强，实际产品模型往往是使用多张曲面进行光滑拼接而成。设计人员在编辑模型形状的过程中对其中一张曲面施加变形约束后，与其相邻的曲面片必须随之做出变形调整，才能保持模型外观的光滑光顺。因此若能设计出一种能够在某张曲面发生约束变形后，其他曲面自适应地做出变形调整以满足连续性的方法将能极大地提高工程人员的设计效率。

过于严格的光滑拼接要求本身并非必要。在工程实践中，当曲面边界的拼接误差在一个可接受的精度要求范围内时，即可认为两张曲面已达到光滑拼接效果，且一般保证拼接边界的G1连续性即可满足绝大多数产品的设计要求。这种允许一定误差的曲面变形技术属于容限造型的范畴，事实上很多几何造型平台均支持容限造型技术。

本文基于CAD/CAM行业的一般理论，提出了一种具有可控误差且保持G1连续的多曲面变形技术，对施加外在约束后的多曲面满足G1连续的协调变形提出了行之有效的算法，摆脱了边界节点矢量必须相同的限制，更具一般性，有重要的学术意义和工程应用价值。最后，以实例验证了本文方法的有效性与正确性。

1 B样条曲面连续性条件

(1)

将4组节点矢量两端均取相应次数加1的重节点个数并进行规范化处理，其余2组节点矢量W与T采取相同处理手段。

对于这样的两张B样条曲面，如果两者满足G0连续，则应满足如下约束条件：

P1(1,v)=P2(0,t)

(2)

式中存在v=v(t)的参数映射关系。该等式的意义为曲面P1(u,v)与曲面P2(w,t)拥有共同的边界曲线。

如果两曲面在边界上满足G1连续，则在满足上述G0连续条件的前提下，还需满足

(3)

图1 连续性条件示意图

2 曲面G0连续拼接

式(2)的G0连续条件为理论上的严格连续条件，根据此条件可给出离散拼接方法。

对曲面片之间的边界进行离散采样。首先需要确定合适的采样个数。众所周知，采样点越密集边界处几何信息越完整，但考虑到计算效率，应将采样点数目控制在合理范围。通常的采样方法为将定义域均分成若干份，参数点以相同的间隔进行取样。对于边界曲线P1(u,v)，其规范化后的节点矢量为V=[v0,v1,…,vn1+kv+1]。

本文采取对每段定义域的中间参数以及定义域的两端点进行采样，以边界曲线P1(1,v)为例，则采样参数序列Q为：

Q={q0,q1,…,qp-1,qp}

(4)

其中每个节点的值为：

(5)

该采样个数确保了边界曲线的每个分段都有采样点。同时定义域两端点也进行采样，确保了边界曲线的起点与终点位置严格约束。

(6)

其中Nj(v)为第j个由节点矢量V=[v0,v1,…,vn1+kv+1]所决定的参数v向B样条基函数。由于上述采样方法确保了参数点数量小于边界待调整控制顶点数，故该方程组为欠约束方程组，有多解，可以用优化的方法获得最优解。

本文的优化目标为曲面片边界处的形状尽量相似。运用文献[7]的思想，目标函数为：

(7)

对于此类带约束问题，运用文献[8]的思想，可采用Langrange乘数法求解，相应的Langrange方程为：

(8)

求方程对各个Langrange乘子与控制顶点各分量的偏导并令其=0，即可获得一组有唯一解的线性方程组。从而获得优化的G0拼接解。

3 曲面G1连续拼接

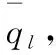
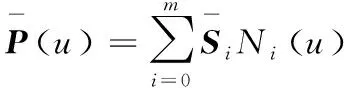
(9)

(10)

图2 等参线控制顶点示意图

由于边界曲线具有Bézier端点性质，根据计算可知，如果节点矢量U的内节点均匀分布，则在u=1处的切矢为

(11)

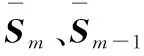
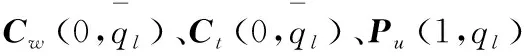
(12)

则曲面必然可以在这点处满足三切矢共面，这是曲面C1连续的条件，自然也能够保证G1连续，且求解条件明晰，方便列出方程组求解。经检验，该方法对曲面变形的调整量较大，且随着节点插入算法的执行，同一点切矢量的值会发生改变，从而等式条件也会发生改变，因此本文不采用C1连续的条件，寻找更优化的满足G1连续的曲面变形调整方案。

ΔPu(1,ql)=P'u(1,ql)-Pu(1,ql)

(13)

图3 跨界切矢调整量

(14)

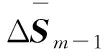
(15)

其中ΔSm-1j(j=0,1,…,n)为待调整曲面第m-1行控制顶点的调整量，是待求解量；Nj为v参数方向的B样条基函数。该方程组为欠约束方程，存在多解，可通过优化的方法获取最优解。

在保证G1连续的协调变形中，待调整曲面形状的改变是不可避免的，基于最小二乘优化原理，优化目标为变形后的控制顶点调整量的平方和最小，因此构建如下目标优化函数：

(16)

这是一个带约束的优化问题，同样采用Langrange乘数法，可构建Langrange方程

(17)

求方程对各个Langrange乘子与控制顶点各分量的偏导并令其=0，即可获得一组有唯一解的线性方程组，从而获得优化的G0拼接解。

4 实例验证

如图4所示，展示了汽车引擎前盖板曲面模型以及在前盖板中间轴线上设置的4个点约束，图5所示为曲面模型变形后的效果。

图4 汽车前盖板曲面模型及多点几何约束

图5 变形后曲面模型

初始汽车前盖板由两片曲面拼接而成，拼接边界为模型中轴线位置，对右半张车前盖曲面边界施加图4所示的4个离散点约束，从而使右半张曲面在靠近中轴线的边界处产生变形，经由本文提出的曲面拼接方法，左半边模型的曲面相应做出变形调整，保证两片车前盖曲面继续保持光滑拼接，最终产生了图5所示的车前盖凸起造型。因此本文多曲面光滑拼接方法的准确性得到了有效的验证。