低压亚超混合层燃油雾化特性数值研究

2020-07-16宫冠吉

机械制造与自动化 2020年3期

宫冠吉

(南京航空航天大学航空发动机热环境与热结构工业和信息化部重点实验室，江苏南京 210016)

0 引言

亚超混合层广泛存在于火箭冲压发动机、超燃冲压发动机等领域，这种流场是通过一股亚声速来流和一股超声速来流混合形成的，其流场结构十分复杂，研究难度大。国外学者对混合层的研究开始得很早，如BOGDANOFF[1-2]等定义了描述混合层特征速度的公式，而国内对于混合层的研究主要是从数值模拟和实验两方面对超声速混合层进行的[3-5]，得到混合层的大涡拟序结构和冷态流场的时空结构。

航空发动机雾化性能的优劣对发动机的各种性能参数有着重要的影响，雾化性能的评价指标主要是索泰尔平均直径和其均匀性的分布[6]。国内学者大量的数值模拟和实验[7-8]研究了不同工况下液滴粒径的变化和均匀性的分布曲线，发现气液质量流量比(即气液比，ALR)、韦伯数、环境压力和喷射角度对雾化性能均有影响。

国内外对于低压条件下亚超混合层的燃油雾化性能的研究很少，因此，本文通过对低压条件下(环境压力：0.01MPa～0.1MPa)不同工况参数亚超混合层的雾化性能进行数值模拟[9]，并分析各参数对雾化性能的影响，总结出有关代表雾化性能颗粒平均索泰尔直径(SMD)的无量纲关系式，从而对后期实验起到指导作用。

1 物理模型与计算工况

本文所使用的物理模型如图 1所示，利用支板将两个流道分隔开来，其中亚声速流道的入口为100mm，超声速流道的入口为16mm，取后端计算域400mm。将直射式喷嘴的直径设置为0.3mm，令喷嘴直径为特征直径，在距离支板末端20mm、50mm、80mm处设置3个不同的喷注位置a、b、c。

图 1 亚超混合层计算模型

图2为剪切层处的网格划分，使用Gambit6.3对亚超大梯度剪切混合层模型进行网格划分，网格划分采用结构化网格，在剪切混合层处进行网格加密处理，划分网格为828 000个。

图2 剪切层处网格划分

2 计算方法与验证

2.1 控制方程

本文采用商用流体力学计算软件Fluent进行数值模拟，计算过程需要求解2位笛卡儿坐标系下的N-S方程，它具有以下形式[10]：

(1)

(2)

(3)

式(1)-式(3)分别为连续性方程、动量方程和能量方程，其中i，j=1，2。式(2)中忽略了体积力做功的影响，u2包括流体自身运动和转子平移运动速度两部分。

求解器选择了基于压力的分离式求解器，流场的迭代方式选用SIMPLEC算法，并选择了RNGk-ε湍流模型。

2.2 破碎模型

对低压混合层燃油喷注过程的数值模拟中启用了液滴二次破碎模型——TAB模型。TAB模型是由AMSDEN A A建立的，将液滴的振动和变形与弹簧质量系统相类比，将空气动力作用视为外力，液体表面张力视为弹性恢复力，黏性视为阻尼力，如图3所示。其中ug为来流速度，R0为原始液滴半径，R为形变后液滴长轴半径。

图3 TAB破碎模型

2.3 验证算例

采用二元低压亚超混合层的试验对数值模拟方法进行验证，实验系统为课题组前期所做工作，模型图如图4所示，其中超声速流道高为16mm，亚声速流道高为100mm，压力测点布置在下壁面。

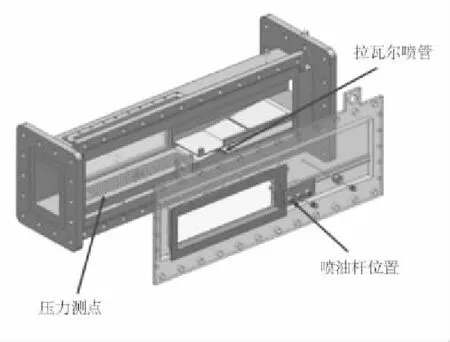
图4 试验件三维模型图

初始边界条件设置与数值模拟过程相同，环境压力设置为0.04MPa，亚声速流、超声速流入口温度分别为300K和548K，马赫数分别为0.1和1.45，压力对比验证选取冷态流场沿流向分布的绝对压力值对比。其中P为绝对压力，x为展向距支板末端的位置。

由于激波的存在，在混合流出口处的位置会产生高低压间隔分布的区域，由图5可以看出，压力分布和颗粒分布对比的趋势基本相同，表明流动结果的可信度较高。

图5 试验与数值模拟结果对比

3 结果分析

3.1 亚超混合层流动分析

图6为混合室的流场结构，横坐标X为距离喷嘴位置，其中图6(a)、图6(b)分别为温度场与速度场，并选取了3个截面得到其速度剖面和温度剖面。从图中可见，两股存在温度梯度和速度梯度的气流在支板末端混合，两种梯度曲线并不单调，气体从低温低速流加速至高温高速流需要一定的区间，首先保持一段低温低速区，其剖面十分平缓，随着展向位置的变化，在一段极小的范围内会迅速加速至高温高速流，这段位置可认为是亚超气体的混合层，继续向超声速流方向发展后，气体会保持高温高速状态。

流向截面的梯度变化也略有不同，最明显处为距支板末端10mm的速度剖面，会产生一部分弯折，这是由于支板的某段存在一小段的回流区。另外其马赫数的峰值也有些许变化，从图6(d)的流场云图可以看出，是因为支板末端的扰动，使得超声速流进入混合室时产生激波。支板末端处由于存在一段低压区，因而会产生膨胀波，膨胀波后总会有压缩波的产生，使压力重回高压，在激波的不断反射过程中，混合室底部会存在交替的高压区与低压区，这就会导致速度的变化。

图6 混合层的主流流场结构

本文在总结了速度梯度曲线后，依据前人的方法定义了混合层的动量厚度为U=U1-Δ0.1U和U=U2+Δ0.1U(U=U1-U2)。

3.2 环境压力对SMD的影响

选取0.01MPa～0.1MPa中典型环境压力，结果显示随着环境压力的增加，燃油雾化后的SMD随之减少，雾化均匀性逐渐降低。在常压状态，燃油的SMD最小，为13.056μm，但是其雾化均匀性最差。典型工况下的SMD分别为72.235μm、46.997μm、29.439μm、20.880μm，相对于常压状态下分别增长了453%、260%、125%、60%。

环境压力的增长导致气流密度增加，因此空气动力作用增加，在燃油颗粒破碎的过程中，表面张力和气动力是主要的影响因素，表面张力维持颗粒形态，而气动力的作用使其变形拉伸。由图7可以看出，当压力增加后，气动力增加使其破碎得更加完全，使SMD逐渐变小，但是SMD的快速下降会使得小颗粒过多，雾化均匀性有所下降。

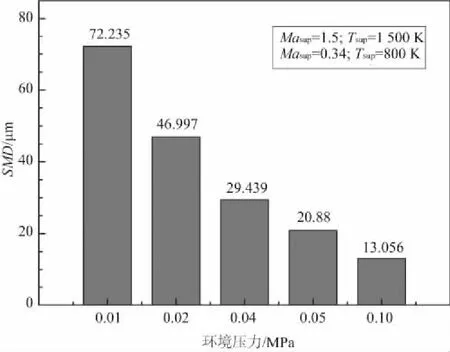
图7 不同环境压力下的SMD变化

图8为液滴数量积分分布和数量累计分布，从图中可以看出，随着环境压力的增加，液滴处于主要积分分布的颗粒逐渐减小，从68μm左右降低至19μm。另外，压力的增加会使得曲线分布更加平缓，小尺寸颗粒数量减小，雾化水平逐渐降低。

图8 不同环境压力下的数量积分分布

3.3 气液质量流量比对SMD影响

燃料在喷注进入气体流道的初始阶段分为表面破碎和液柱破碎，决定破碎方式的是雾化性能另一个关键的无量纲数是气液比ALR，表达式为：ALR=ma/ml。其中ml、ma分别为液相与气相的质量。

从图9可以看出，随着气液比的增加，喷雾粒径φSMD逐渐变小且变化趋势有逐渐减缓的趋势。一方面，在气液比增加后，空气与燃料的速度差所引起的气动力随之增加，空气能够克服液体表面张力，使得液团破碎成为更小的液滴。另一方面，气液比的增加使得液柱的初始扰动有所增加，这能快速形成表面波从而使液柱破碎。

图9 ALR对SMD的影响

3.4 韦伯数对SMD影响

图10为韦伯数分别为150.404、148.105、143.560条件下，3个不同位置直射式喷嘴的SMD计算结果。可以看到，随着韦伯数的增加，SMD近似呈线性减小，但是随着喷嘴位置的向后推移，SMD是在逐渐增大。图11则显示韦伯数的增加使得体积分数曲线更加平缓，雾化破碎效果更好，颗粒直径分布得更加均匀。

不同的韦伯数下主要为气液间的相对速度影响着两者气动力和表面张力的平衡。液滴是否发生二次雾化主要取决于韦伯数的大小，当韦伯数大于临界韦伯数时，气动力的作用将超过维持液滴表面的表面张力，从而发生袋式破碎、剪切破碎或者爆炸破碎。随着韦伯数的升高，两者的相对速度在不断地增加，这也导致了气液两相间的气动力增长，破碎更加完全，雾化性能提升。