波纹叶片控制扩压叶栅流动分离的DES数值模拟

2020-07-16苏丽蓉羌晓青

节能技术 2020年1期

苏丽蓉，羌晓青,2

(1.上海交通大学航空航天学院，上海 200240; 2.燃气轮机与民用航空发动机教育部工程研究中心，上海 200240)

近些年来，航空发动机正朝着高推重比的目标发展，为尽量减少压气机级数，分配到每级的负荷势必显著增大[1]。在提高压气机负荷的同时，有必要采取流动控制技术抑制叶片表面的气流分离。波纹叶片是一种起源于仿生学的新型被动流动控制技术。海洋生物学家发现，座头鲸肢状鳍前缘的圆齿型结构能帮助座头鲸在做急转运动、捕食行为中保持较高的升力而不致失速[2]。受此启发，Watts和Fish[3]首先提出采用波浪型前缘仿生学翼型(以下简称“仿生学翼型”)提高风力机叶片的升力，验证了仿生学翼型升阻比在10°攻角下提高了17.6%。Miklosovic等[4]对座头鲸肢状鳍模型的试验研究表明，圆齿型凸起可将最大升力系数提高6%，失速攻角扩大40%。Pedro等[5]通过数值研究发现圆齿型结构可延缓分离区由翼尖向根部扩散的趋势。Johari等[6]对不同波长、波幅组合的仿生学翼型性能进行了数值研究，结果表明波幅是影响波纹翼型性能的主要设计参数。Skillen等[7]认为，波纹前缘的展向压力梯度诱导产生的二次流提高了波峰下游的附面层能量。Hansen等[8]和Perez-Torro等[9]分别对流向涡的径向位置变化及其作为层流分离泡与相邻完全分离剪切层之间交界面的演化过程进行了详细研究。

近五年来，有学者开始将仿生学叶片应用于压气机叶栅中，开展了相关的试验和数值研究。Keerthi等[10-11]在平面叶栅试验中的研究表明，仿生学叶片的失速攻角扩大了43%，很大程度上改善了叶栅性能。郑覃等[12]在环形叶栅中进行的数值研究表明，仿生学叶片诱导产生的对转旋涡与角区分离涡相互作用，可有效改善叶栅端区流动。屠宝锋等[13]在跨音速压气机中进行的数值研究表明，对转涡结构可形成局部分离延缓效应。王博等[14]在高负荷扩压叶栅中的数值研究表明，仿生学叶片在中径处可减小流动分离、缓解通道堵塞。

如上所述，目前的仿生学叶片研究主要集中在外流孤立叶片，而在扩压叶栅中的应用研究起步较晚，国内外研究成果较少。因此，本文在仿生学叶片的研究基础上，提出一种应用于扩压叶栅中的新型波纹叶片设计方法，探索其控制叶栅流动分离、降低气动损失的可能性。本文将以准三维平面叶栅为研究对象，在典型攻角工况下对原型叶栅和波纹叶片叶栅进行高保真度的DES数值模拟，研究波纹叶片对扩压叶栅性能的影响，探索叶片表面波纹诱导产生旋涡的非定常流动现象，对波纹叶片控制扩压叶栅流动分离的机理进行初步探讨。

1 计算模型及数值方法

1.1 计算模型

选取亚音速大折转角扩压叶栅作为基元叶型，通过径向积叠得到原型叶栅，进口马赫数为0.50。表1给出了与该基元叶型相关的主要几何参数，其中，角度均定义为与轴向的夹角。

表1 基元叶型主要几何参数

参数值进口马赫数M10.50弦长c/mm60安装角γ/(°)14.27稠度s1.667进口几何角β1r/(°)37.95出口几何角β2r/(°)-2.18

本文的研究对象为波纹叶片，波纹叶片由叶型相同、弦长不同的波峰、波中、波谷3个截面经尾缘积叠而成，主要设计参数包括波数N、波长W和放大系数k。其中，波长W定义为两个相邻波峰之间的径向距离，放大系数k定义为波峰与波中弦长之比，即

k=ccrest/cmiddle=cmiddle/ctrough

(1)

以往研究的仿生学叶片均带有前缘凸起、表面平滑的几何特征[11-14]，而本文所研究的波纹叶片具有完全不同的几何特征，除了前缘同样具有凸起特征外，波纹叶片的吸力面和压力面侧均带有周期性波纹，由于采用尾缘积叠的缘故，波纹由前缘向尾缘逐渐趋于平缓。经过设计参数选取的预研究，本文最终选定波数N=3，放大系数k=1.005，波长W=6.67%c的波纹叶栅作为研究对象，展弦比为0.2，几何模型如图1所示。

图1 波纹叶片几何模型

1.2 数值方法

本文使用商业软件NUMECA FINE/Turbo 12.2进行数值模拟，采用基于Spalart-Allmaras的分离涡模拟(DES)湍流模型，分别对原型叶栅和波纹叶栅在0°攻角和8°攻角工况进行数值模拟。计算网格由AutoGrid/IGG模块生成，由于DES湍流模型对于计算网格的要求较高，因此在重点研究的吸力面侧及叶片前缘附近对网格进行加密，最终采用的网格径向网格点数为105，网格总数为505万，第一层网格距离固体壁面0.001 mm，保证叶片表面y+值始终小于1。

计算域和网格拓扑结构如图2所示，在进口给定总温、总压和气流方向，出口给定大气压，通过改变进口参数保证进口马赫数为0.5不变。上下端壁为周期边界条件，叶片表面为绝热无滑移固壁边界条件，通道两侧取周期性平移边界条件以保证相邻叶片通道间的连接。使用已收敛的RANS定常结果作为初场，设置物理时间步长为Δt=1×10-5s。在吸力面近前缘区域选取气动探针监测点，待监测点静压达到稳定波动后继续计算2 000步，并将此期间内的流场做时间平均处理，得到时均参数，监测点静压波动曲线如图3所示。

图2 准三维平面叶栅计算域及B2B拓扑结构

图3 吸力面监测点静压波动曲线

为验证本文数值方法的可靠性，在上海交通大学平面叶栅试验台上对原型叶栅进行吹风试验，测量50%叶高的叶片表面静压分布，并与DES数值结果进行对比，如图4所示。由图可见，0°攻角下的数值结果与试验结果吻合较好，而8°攻角下DES模拟的压力面静压相比试验结果偏高，但是曲线趋势基本一致，偏差在可接受范围内。因此，本文所采用的DES数值方法以及计算结果具有一定的合理性和可靠性。

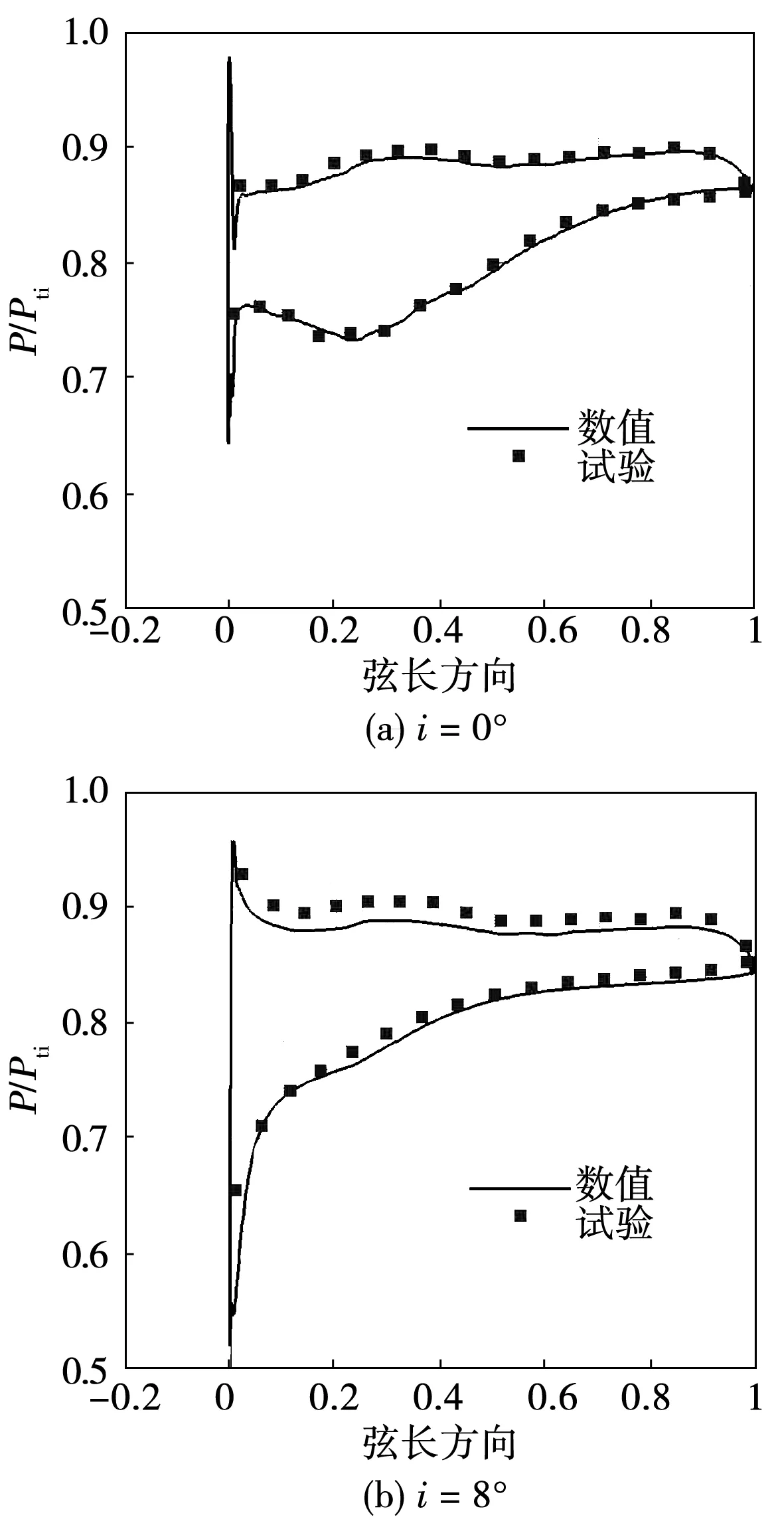
图4 叶片表面静压分布

2 计算结果与分析

2.1 叶栅总体性能

为研究波纹叶片扩压叶栅的总体性能，表2、表3分别给出了原型和波纹叶片分别在0°、8°攻角下的时均性能参数对比。用总压损失系数TPLC来衡量叶栅损失大小，定义如下

TPLC=(Pt1-Pt2)/(Pt1-P1)

(2)

式中Pt1、Pt2和P1——叶栅进口总压、出口总压和进口静压。

表2 时均性能参数对比，i=0°

方案总压损失系数气流折转角扩压因子原型0.021 437.310.172 1波纹叶片0.021 537.260.171 4

表3 时均性能参数对比，i=8°

方案总压损失系数气流折转角扩压因子原型0.108 742.350.205 6波纹叶片0.098 942.620.212 3

从表2可以看出，在0°攻角下，波纹叶片扩压叶栅的性能参数均与原型叶栅非常接近，表明波纹叶栅设计并未由于加剧流场的三维流动特性而引入过多的额外损失。由表3可知，在8°攻角下，波纹叶栅的总压损失系数相较于原型叶栅降低9.02%，扩压因子增大3.15%，气流折转角有所扩大，表明叶栅扩压能力得到一定程度的恢复。综合考虑两个攻角下的性能参数可初步得知，波纹叶片设计在大攻角下起到降低叶栅损失的作用，同时在设计攻角下不造成明显的额外损失，是一种较为理想的流动分离控制措施。

2.2 吸力面附面层分离

图5给出了0°攻角下的零轴向速度等势面，显示出流动分离区。由图可以看出，原型叶栅的吸力面分离区仅存在于前2%弦长以及尾缘附近的小范围回流区内。而在波纹叶栅中，前缘分离区在径向上呈现明显的周期性，且分离区域相对集中在波谷下游，尾缘回流区同样呈周期性波纹状。结合表2中的分析，波纹叶栅虽然改变了分离区的分布形式，但是对总压损失系数几乎没有产生影响。

图6给出了8°攻角下的叶片吸力面流动分离区。在该攻角工况下，原型叶栅吸力面出现严重流动分离，分离区范围覆盖10%弦长位置上游以及32%弦长位置下游。在波纹叶栅中，10%弦长上游的近前缘区域流动分离得到缓解，波峰下游处的前缘分离泡几乎完全消失，而波谷下游处的分离泡依然存在，但相较原型叶栅也有明显减弱。值得注意的是，由于大攻角工况下的流场复杂性增加，波纹叶栅流场不再呈现明显的径向周期规律，尤其是在上下两个周期面附近的周期性较差，在不同径向截面的分离起始点轴向位置差异也较大。

图5 叶片吸力面流动分离区，i=0°

图6 叶片吸力面流动分离区，i=8°

2.3 涡结构

Q=((2-tr(

(3)

式中 tr——矩阵的迹。

从图7中可以看出，0°攻角下，波纹叶栅吸力面、压力面附近均存在相对稳定的旋涡结构，压力面50%弦长位置处还存在细小的近壁面涡层。此外，尾缘附近的脱落涡呈现出类似于卡门涡街的两排交替形成的双列线涡。在t=1/4T时刻，尾缘分离涡开始脱落形成小涡团，随时间推移沿流向发展且尺度逐渐增大，随着涡团与主流掺混耗散，涡团尺度逐渐减小直至消失。至t=4/4T时刻，新的小涡团开始从尾缘脱落形成，进入下一个周期。

图7 波纹叶栅Q=100 000等势面，i=0°

由此可见，虽然波纹叶片设计对流场有一定的额外扰动，但是流场复杂性并未明显增加，流场中的涡演化主要来自尾缘脱离涡，且呈现明显的周期性。

图8给出了8°攻角下波纹叶栅流场内的Q等势面在一个时间周期内的变化过程。

图8 波纹叶栅Q=100 000 000等势面，i=8°

如图所示，8°攻角下，从前缘开始产生的吸力面分离涡拉伸成细长条的流向结构，从1/4T至3/4T时刻，可看到较大尺度的涡团逐渐脱落，并汇入尾缘附近的涡系。80%弦长位置附近存在一些细小涡结构以及近壁面涡层。此外，尾缘附近还存在较大尺度的尾缘脱落涡，与吸力面的分离涡产生周期性融合，并在向下游移动过程中急剧耗散。8°攻角下叶栅非定常流动现象比0°攻角下具有更复杂的三维流动特性。一方面，前缘附近积聚大量的旋涡结构，形成流向涡结构的脱落以及局部的能量传输，另一方面，尾缘脱落涡不再呈现相对规整的双列线涡，而是表现为由尾缘脱落涡和吸力面分离涡产生的周期性融合。

为进一步了解波纹叶栅的前缘局部非定常流动，图9给出了原型叶栅和波纹叶栅流场内的Q=100 000 000等势面，并以轴向涡量ωz着色。

从图9来看，原型叶栅的前缘至30%弦长范围内存在近壁面分离涡，涡量较小，而尾缘处回流区的涡系更为明显。相比之下，波纹叶栅诱导产生的旋涡在前缘至30%弦长范围内有明确的发展轨迹，多呈现为流向结构。波纹叶栅诱导产生的反向旋转的对涡结构增强了前缘的局部流动，流向涡在向下游发展的过程中为前缘附面层低能流体注入动量，同时阻碍低能流体的横向迁移，改变了前缘损失区域的范围。结合图5分析得到，前缘形成的分离涡积聚在每个波谷的下游处，且在波谷两侧发展为旋转方向相反的一对流向涡。此外，前缘流向涡脱落后与尾缘附近涡系的周期性融合也为尾缘附近的附面层低能流体注入动量，提高其抗分离能力。