GPS/BDS下ARAIM的可用性验证和卫星的故障检测*
2020-07-15刘瑞华董開琳
刘瑞华 董開琳 王 剑
1.中国民航大学电子信息与自动化学院,天津 300300 2.民航航空器适航审定技术重点实验室,天津 300300
0 引言
2012年,《国务院关于促进民航业发展的若干意见》指出:推动北斗导航卫星系统(BDS)在民航领域的应用。截止到2018年12月27日,北斗三号正式向全球提供基本导航服务,BDS迈入全球时代。为了积极响应国务院的号召,必须首先满足民航运行最看重的一个点:“安全性”。一般来讲,对于民航用户,主要是通过确保导航系统的完好性,来保证飞机飞行的安全。
高级接收机自主完好性监视(Advanced Receiver Autonomous Integrity Monitoring, ARAIM)是接收机自主完好性监视(Receiver Autonomous Integrity Monitoring, RAIM)的进一步提高和拓展。相较于RAIM只能提供水平方向的完好性监视服务,ARAIM则可以在进近阶段为飞机提供垂直方向的完好性监视服务,最多可以支持将飞机以规定的所需导航性能(Required Navigation Performance, RNP)引导至距地面200英尺的高度,即LPV-200 (Localizer Performance with Vertical guidance-200 feet)[1]。
当前,国内外对ARAIM的仿真研究绝大部分是基于全球定位系统(GPS)和格洛纳斯(GLONASS)或伽利略(GALILEO)组合系统进行的,很少涉及到我国自主研发的BDS。因此,为了弥补ARAIM在BDS下仿真研究的空白,为了给ARAIM在民航领域应用做一定的铺垫,在GPS/BDS下分别研究了ARAIM在亚太范围内的可用性和ARAIM算法故障检测的性能。
1 ARAIM的导航要求
1.1 LPV-200的完好性性能要求
基于现有的相关标准,LPV-200的完好性性能要求主要有以下4个[2]:
1)水平保护级(Horizontal Protection Level, HPL)小于水平告警门限(Horizontal Alert Limit, HAL);垂直保护级(Vertical Protection Level, VPL)小于垂直告警门限(Vertical Alert Limit, VAL)。
2)有效监视门限(Effective Monitoring Threshold, EMT)小于等于15m。
3)垂直导航系统误差(Vertical Navigation System Error, VNSE)在95%的时间里小于4m。
4)告警时间小于6s。
要求1)在LPV-200的完好性性能要求中最为重要,安全等级最高。
除此之外,ARAIM有一个明显的优点,就是不用满足告警时间小于6s的要求,因为ARAIM算法没有将全部的计算都放在地面,而是分配到航空设备当中。因此,不用地面在6s内给用户告警[3]。
1.2 ARAIM的可用性判据
由1.1可知,当计算结果满足以下3个条件时,说明ARAIM是可用的。
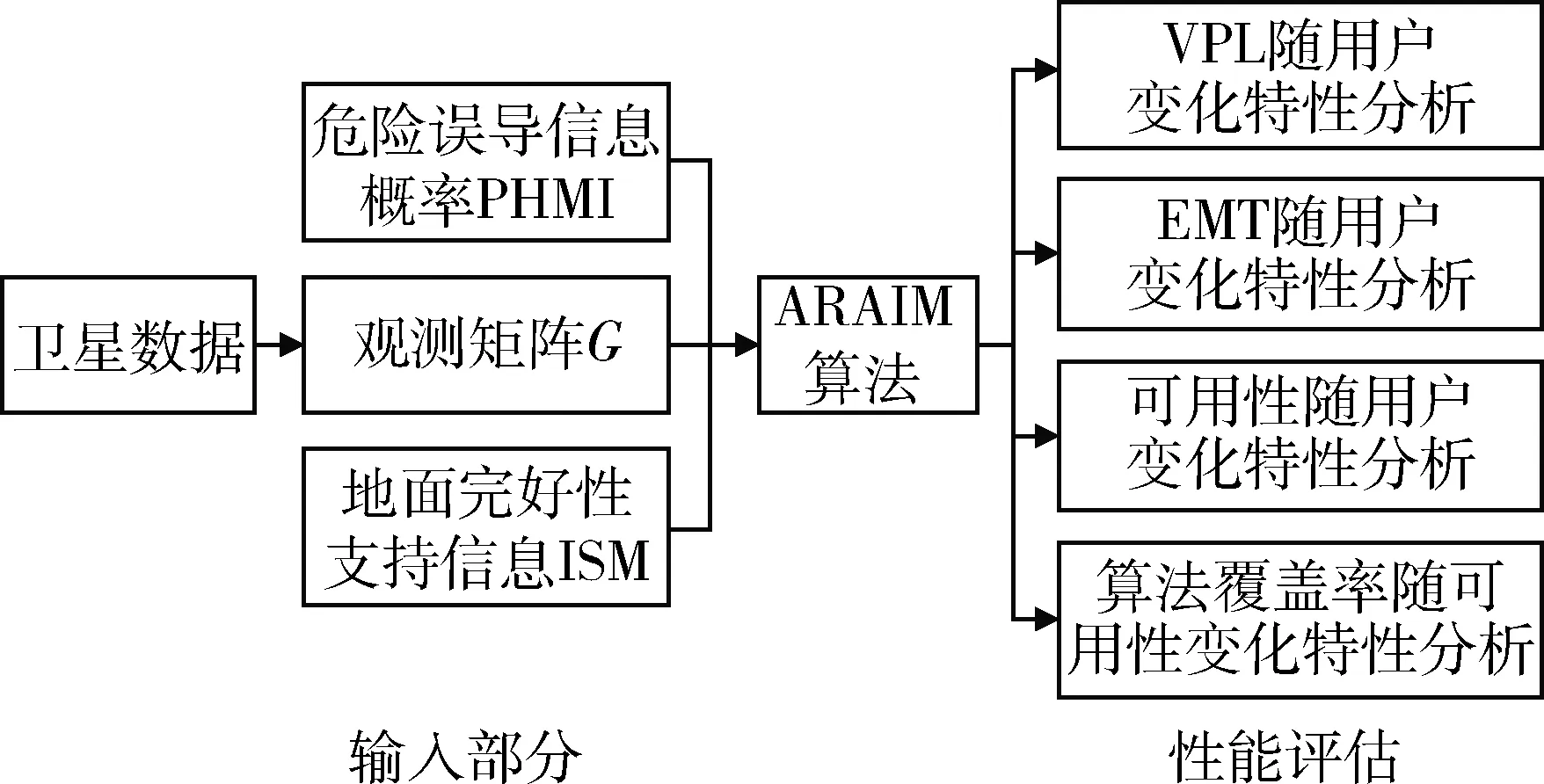
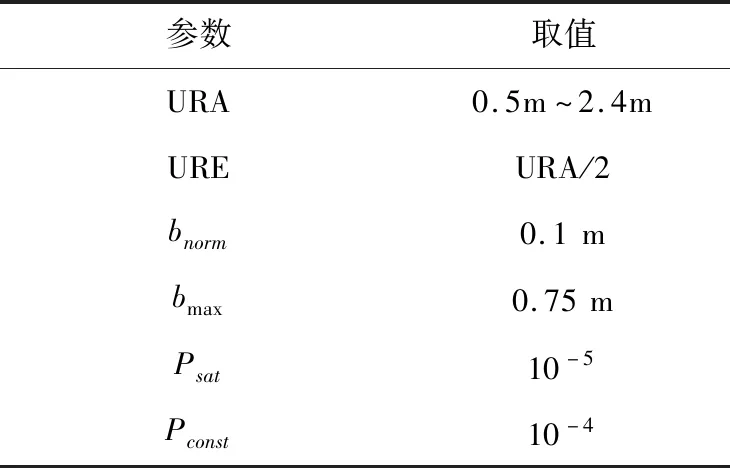
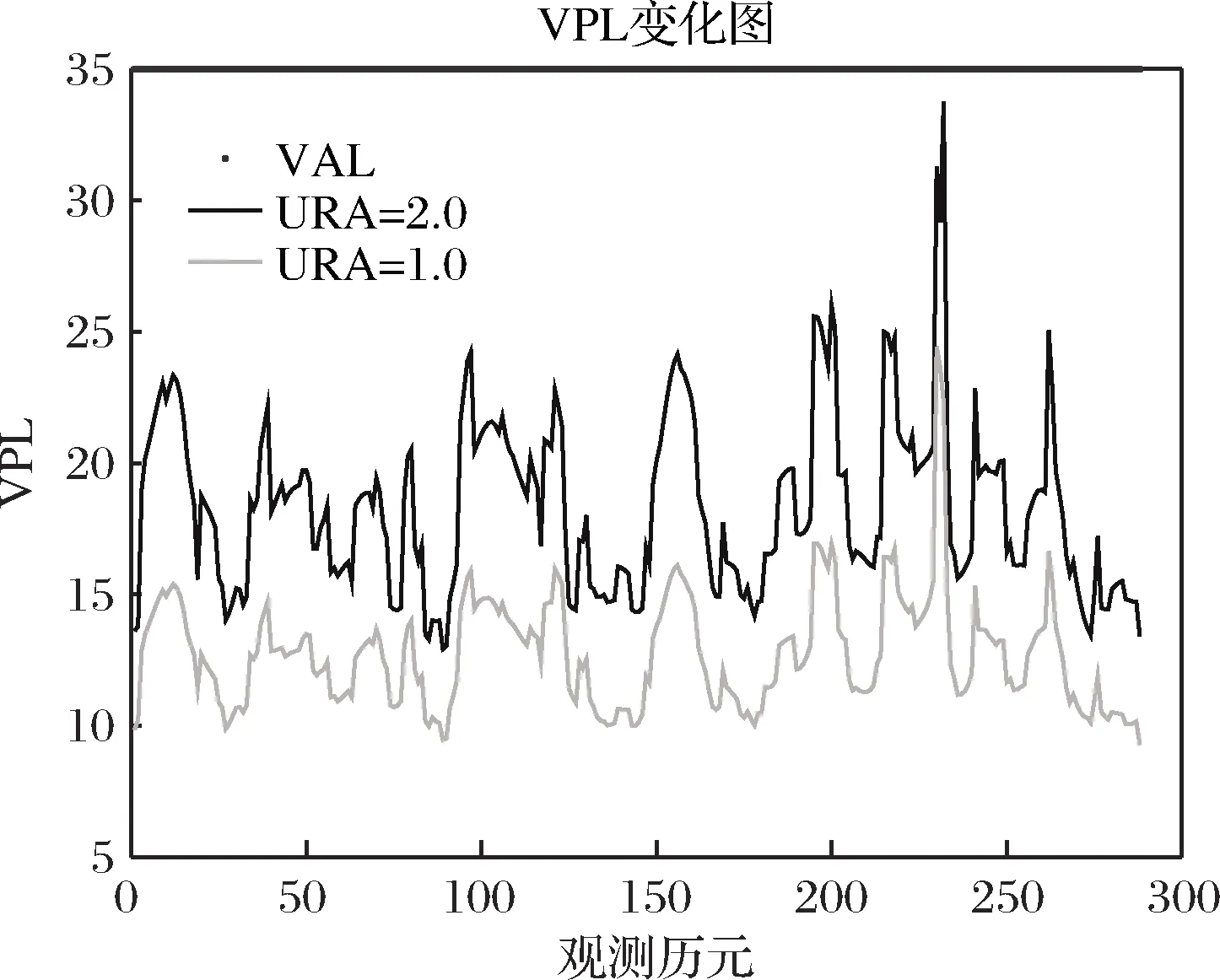
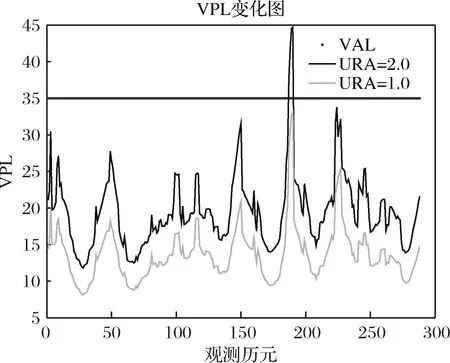
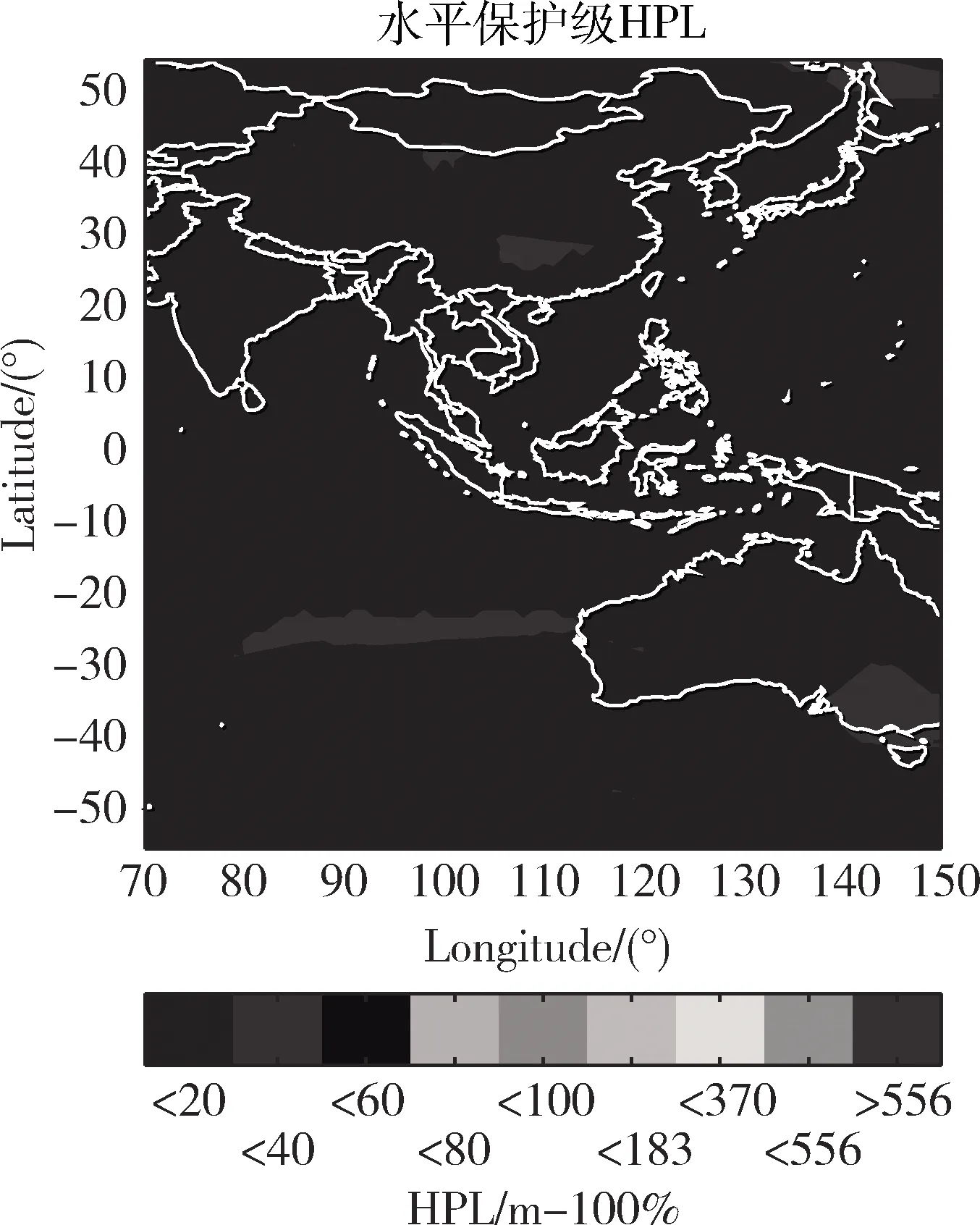
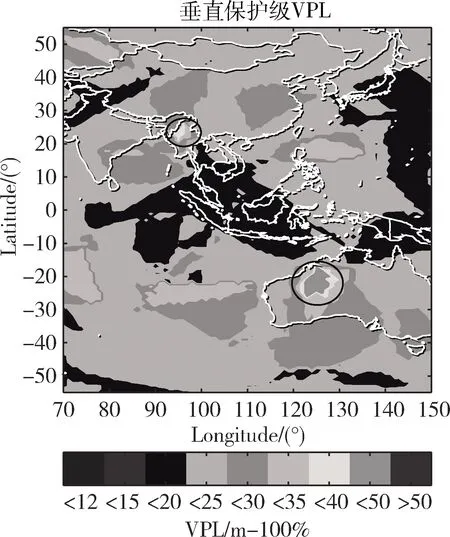
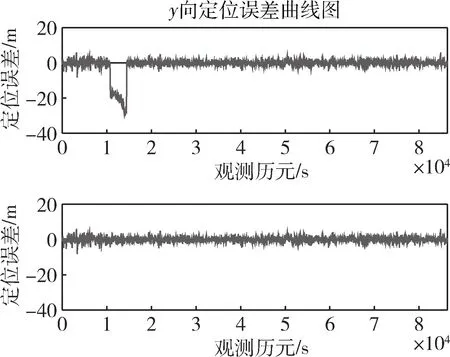
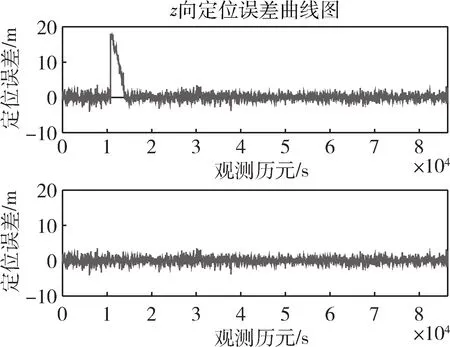
1)HPL 2)EMT=max{Dk}≤15m; 3)95%的时间里VNSE<4m; 其中1)是判断ARAIM是否可用的主要条件, 2)和3)不被强制。因此,在仿真和实际应用中,可以通过最小化HPL和VPL来最大化满足ARAIM的可用性[4]。 ARAIM的整体架构如图1所示,主要包括输入部分,ARAIM算法部分和性能评估部分[5]。 图1 ARAIM的整体架构 输入部分包括危险误导信息概率(Probability of Hazardously Misleading Information, PHMI),通过接收卫星实测数据所获得的观测矩阵G,以及地面完好性支持信息(Integrity Support Message, ISM)。 ISM是基于星座运行的历史,分析其表现和性能所总结出来的,用于表征卫星和星座在正常和故障状态下的伪距精度和先验概率[6]。 当前,ISM包含的参数以及参数的大小都还在研究讨论当中,但是一般来讲,它主要包含以下6个参数,如表1所示。 表1 ISM包含的各个参数 1)用户测距精度(URA):是指由卫星部分和地面部分引起的测距误差,用来评估ARAIM算法的可用性。取值范围通常为0.5~2.4m。 2)用户测距误差(URE):是指卫星信号在空间的误差估计。取值通常为URA的一半。 3)连续性偏差(bnorm):也称为标准偏差,用来评估系统的精度和连续性。 4)完好性偏差(bmax):也称为最大偏差,用来评估系统的完好性。 5)卫星故障概率(Psat):是指卫星发生故障的先验概率。 6)星座故障概率(Pconst):是指星座发生故障的先验概率。 基于多假设分组解(Multiple Hypothesis Solution Separation, MHSS)的ARAIM算法不用计算误警率、漏检率以及检测门限,而是直接根据具体飞行阶段对导航系统的完好性要求来计算保护级,即ARAIM算法通过保证PHMI来满足完好性要求[7]。 根据卫星导航定位原理,对导航系统的观测模型进行线性化处理可得: y=Gx+ε (1) 式中:y为观测伪距与线性化伪距预测值之间的差值;G为观测矩阵;x为用户状态矢量,是用户的三维位置及时钟与标称值之间的偏差;ε是测量误差矢量,假设它的所有元素均服从零均值的高斯分布[8]。 (2) (3) 式中:σURA,k表示地面检测部分造成的钟差和星历误差的标准差;σtropo,k表示信号传输过程中对流层延时误差的标准差;σuser,k表示接收机噪声和多径效应的标准差。 (4) 式中:Mk为第k个对角线元素置0的单位矩阵;Sk为假定第k颗卫星为故障卫星时的加权最小二乘投影矩阵。 因此,第k颗卫星的检验统计量为: (5) 检测门限为: (6) 式中:Kffd,k为连续性约束系数;ΔSk=Sk-S0。 Kffd,k=-Q-1(Pfa/2n) (7) 式中:Q-1为标准正态累积分布函数的逆函数;Pfa为连续性风概率。Kffd,k是将Pfa平均分配到n颗可见星上得到的。 对比检验统计量和检测门限,若dk>Dk,则认为检测到了故障[9]。 在基于MHSS的ARAIM算法中,VPL的定义如下: VPL=max{VPL(0),VPL(k)},k=0,…,n (8) 式中:VPL(0)为n颗可见星均处于无故障状态下的VPL;VPL(k)为假定第k颗卫星为故障卫星时,排除第k颗故障卫星后的VPL。 (9) (10) 式(9)和式(10)中:Kmd,0为无故障条件下的完好性风险约束系数,Kmd,k为第k颗卫星故障条件下的完好性风险约束系数。 Kmd,0和Kmd,k的计算公式如下: (11) (12) 式(12)中:Psat,k为第k颗卫星的故障概率。 PHMI(0)和PHMI(k)需满足以下条件: (13) 基于MHSS的ARAIM算法采用平均分配的方式将PHMI分配到n颗可见星上可得: (14) (15) 将式(7)、式(14)和式(15)代入式(9)和式(10)就可以计算出VPL (0)和VPL (k),从而得到VPL[10]。 ISM作为ARAIM最主要的输入参数,会对ARAIM的可用性造成一定的影响,而ARAIM的可用性最直观的体现就是VPL的大小。在ISM的所有参数中,URA最为重要,因此,首先探究URA对ARAIM可用性造成的影响,接着再进行ARAIM的可用性验证。 以天津市(39°N,117°E)和格尔木市(36°N,94°E)为例,利用2019年12月6日8时的历书数据,设置卫星遮蔽角为5°,URA为1.0m和2.0m,其它ISM参数值的大小如表2所示。计算2019年12月6日8时至2019年12月7日8时这24h内天津市和格尔木市的VPL,采样间隔设为5min。 表2 ISM参数值的设置 仿真结果如下: 由图2和图3可以看出,在天津市和格尔木市,URA为2.0m时的VPL明显比URA为1.0m时的VPL大;但是在天津市,2个不同的URA下,VPL均小于VAL,而在格尔木市,URA为2.0m时有部分时间的VPL大于VAL,不能完全满足LPV-200的完好性性能要求。 图2 天津市不同URA下VPL的变化 图3 格尔木市不同URA下VPL的变化 由此可知:在双频条件下,电离层误差已经基本被消除,系统的可用性很大程度上取决于URA,在仿真和实际应用中,可以通过确定更精确的伪距测量误差模型来提高URA,从而获得更小的VPL,提高系统的可用性。 ARAIM的可用性是针对LPV-200的完好性性能要求而言的,因此,在进行ARAIM的可用性验证时,主要考虑HPL和VPL的要求。 以亚太范围为例,将经纬度间隔设为1°×1°,利用2019年12月8日8时的历书数据,设置卫星遮蔽角为5°,URA为1.4m,其它ISM参数值的大小如表2所示。对2019年12月8日8时至2019年12月11日8时这72h内亚太范围内ARAIM的可用性进行验证,采样间隔设为5min。 该仿真过程共有865个采样点,图中的100%表示以这865个采样点中计算所得的最大值作为作图依据,以此保证仿真结果的可靠性。 仿真结果如下: 由图4可以看出,在72h的仿真时长内,亚太范围内的HPL均小于HAL,完全满足LPV-200的完好性性能要求;由图5可以看出,在72h的仿真时长内,亚太范围内的VPL在两个小黑圈所标注的地方略大于VAL,其它区域的VPL完全满足LPV-200的完好性性能要求。 图4 GPS/BDS下亚太范围内的HPL 图5 GPS/BDS下亚太范围内的VPL ARAIM在亚太范围内的可用性覆盖率达到90%以上,验证了ARAIM的可用性。 之所以有部分区域未满足要求,是因为在仿真时,URA的取值为1.4m,比ARAIM技术工作组(ARAIM Technical Subgroup, ARAIM TSG)规定的URA的取值大0.4m。而且是以计算得到的最大的VPL作为作图依据,难免会在72h的仿真时长内,出现1、2个采样点的VPL大于VAL的情况。 为了确保导航系统能够向用户提供准确的导航定位服务,ARAIM算法需要及时对出现故障的卫星进行检测与排除。 以格尔木市(36°N,94°E)为例,设置卫星遮蔽角为5°,统计格尔木市2019年12月1日8时至2019年12月2日8时这24h内的BDS可见星数量。由统计结果可知,编号为1到5号的地球同步卫星始终存在于观测时长内。因此,在2号卫星上添加一个幅值为100m的“阶跃型”伪距误差,模拟2号卫星出现故障,然后利用ARAIM算法对存在故障的卫星进行检测与排除。 仿真结果如下: 由图6~8可以看出,当导航系统的卫星存在幅值为100m的“阶跃型”故障时,用户的定位误差明显变大,利用ARAIM算法对存在故障的卫星进行检测与排除后,重新计算得到的用户定位误差回归正常。 图6 故障检测与排除前后x向的定位误差 图7 故障检测与排除前后y向的定位误差 图8 故障检测与排除前后z向的定位误差 ARAIM算法准确检测出了存在故障的卫星,说明了ARAIM算法故障检测的性能良好。 针对ARAIM在BDS下仿真研究的空白,本文基于实测数据,在GPS/BDS下,验证了ARAIM的可用性,利用ARAIM算法成功对卫星的故障进行了检测与排除。由仿真实验的结果可知,ARAIM在亚太范围内的可用性良好,ARAIM算法故障检测的性能良好。因此,ARAIM完全可以在将来应用于民航领域,为民航提供高标准的完好性监视服务。 后续工作可以从多系统组合下ARAIM的研究着手,而不是仅限于GPS/BDS组合系统。还可以试着改进ARAIM算法,对保护级的计算方法和故障检测的方法进行优化。2 ARAIM的实现原理
2.1 ARAIM的整体架构

2.2 基于多假设分组解的ARAIM算法
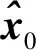
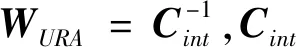

2.3 垂直保护级的计算
3 仿真校验
3.1 URA对ARAIM可用性的影响
3.2 ARAIM的可用性验证
3.3 卫星的故障检测

4 结论
