横列式直升机纵向鲁棒控制系统设计及半实物仿真

齐 浩 王泽河 杨 骁 朱纪洪

1.河北农业大学 机电工程学院，保定071001 2.清华大学 计算科学与技术系, 北京 100804

0 引言

重量、重心作为直接影响飞行器的过载性能、操作稳定性等指标的基本状态参数[1-2]，为保证飞行器在不同重量、重心状态下满足飞行重心包线要求，需对飞行器重心进行调节[3]，然而传统飞行器重心调节方法多为预先重心调节及配重调节法，虽然解决了大重心变化的调节问题，但对燃油面变化等因素造成的小幅度、高频次重心变化没有较好的解决办法[4-6]，因此本文通过基于同伦连续原理修改的Nelder-Mead Simplex优化算法得到了横列式直升机的配平条件，并以此为基础提出了一种基于角加速度估计补偿的强鲁棒控制方法。

1 横列式直升机纵向模型

横列式直升机旋翼系统产生的力随旋翼变距的变化是一个非线性动态过程[7-8]，此过程最终稳定于一个高频小振幅极限环上，此非线性动态过程的上升段类似于一阶线性动态，可以直接采用旋翼力作为控制输入[9-10]，得到飞行器的简化模型。

如图1所示，n为俯仰角，T为桨盘拉力，FTxb和FTzb为桨盘拉力在机体坐标系上的投影，β为输入桨盘纵向倾角，DA为飞行器产生的气动总阻力，LA为飞行器产生的气动总升力，mA为飞行器产生的总气动俯仰力矩，l1和l3分别为从短舱根部到重心和短舱顶端的长度大小，ξ为桨盘拉力方向与地面的夹角，V为飞行器飞行速度，γ为飞行器航迹倾斜角度。其它符号意义参见前后文或符号表。

图1 横列式直升机纵向结构和受力情况示意图

横列式直升机纵向数学模型根据刚体三自由度运动方程，其中，θ为以地面坐标系为基准，飞行器俯仰角的大小，q为以机体坐标系为基准，俯仰角速度的大小，Vxg和Vzg为以地面坐标系为基准，水平和垂直速度的大小。

(1)

式(1)中：Iyy为飞行器产生的纵向转动惯量，mT为桨盘总拉力，为飞行器提供俯仰力矩，FTxg和FTzg为以地面坐标系为基准，桨盘拉力合力产生的投影，FAxg和FAzg为以地面坐标系为基准，飞行器空气动力合力产生的投影，由此推得：

(3)

将式(3)代入式(2)，可以得到横列式直升机的纵向数学模型(4)。

(4)

2 配平分析

通过配平分析，可以对飞行器不同飞行工况的特性进行定量分析，为控制方法的设计奠定基础。

2.1 非线性直接搜索优化算法

Nelder-Mead Simplex算法是一种用于求解非线性方程最小值问题的直接搜索方法。因为求解飞行器气动力和力矩部分的非线性方程没有解析解，无法取得直接的梯度信息，通常需要通过查询数据表格得到，因此，配平分析过程可以采用Nelder-Mead Simplex算法。

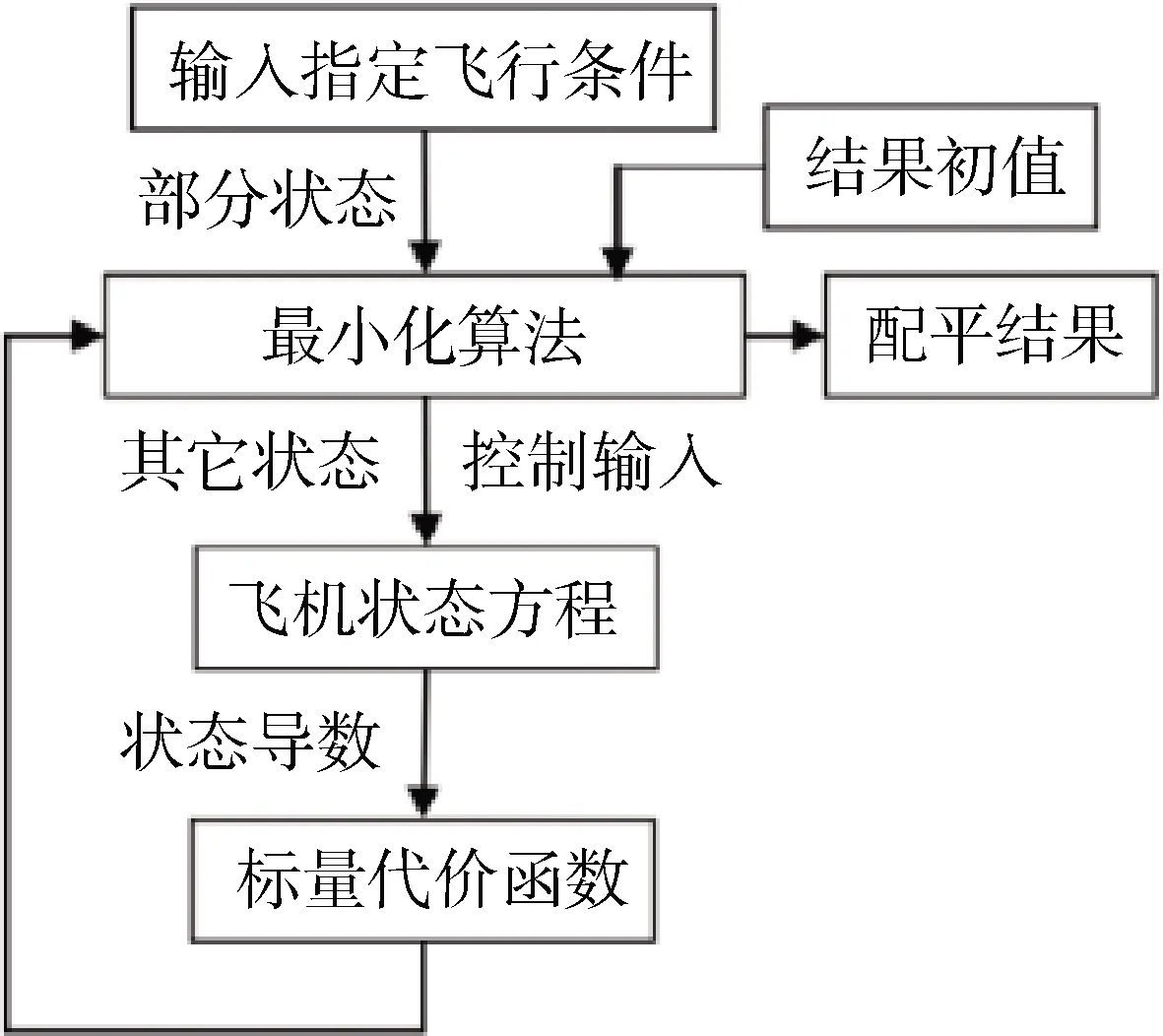
图2 配平方法流程图

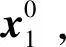
2.2 基于同伦连续原理的优化算法

基础Nelder-Mead Simplex算法是一种局部收敛算法，算法运行过程中，当给定初值不合适时，代价函数极易在局部极值点收敛。因此，本文在基础Nelder-Mead Simplex算法上基于同伦连续原理进行了修改，解决了对初值敏感的问题。

同伦连续法为克服牛顿迭代法局部奇异性的缺陷，通过对非线性方程组f(x)=0，x∈Rn，f:Rn→Rn嵌入一个凸线性全域同伦矢量函数，推导出：H(x,t)=tf(x)+(1-t)g(x)=0，式中，t是同伦参数，则g(x)=0的解易知。显然，t=0时g(x)=0的解能满足方程组H(x,0)=0，而通过t=1时H(x,1)=0的解可以推导出f(x)=0的解。

基于同伦连续法的Nelder-Mead Simplex算法，将求解目标非线性方程组中的某参数作为同伦参数，即，目标函数为F(c,x)=0，其中，F=(F1，F2，…，Fn)T，选取常数c作为一个标量参数，则c的初值c0使得F(c0,x)=0的解易知，通过将这个易知解作为迭代初值，计算F(c0+dc,x)=0的解，再重复上述步骤进行类推，推导得出F(c,x)=0的解。根据图3所示对比结果，修改后的算法更为高效。

图3 修改后算法与基础算法计算结果对比

2.3 配平结果分析

通过上述优化算法，求解横列式直升机在不同工况下的配平条件。图4是横列式直升机不同速度时，俯仰角n、桨盘拉力T、输入桨盘纵向倾角β的配平条件。

图4 不同速度时，俯仰角的配平条件

图5 不同速度时，拉力的配平条件

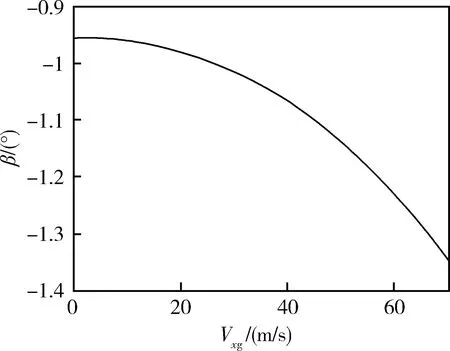
图6 不同速度时，桨盘纵向倾角的配平条件

3 增强纵向稳定性强鲁棒控制方法

3.1 影响飞行器纵向稳定性因素

根据确定规则的控制器(简称RB控制器)和串联混合动力系统。RB控制器通过比较电机返回的需求功率和发电系统可产生的功率，结合当前电池组电量，控制发动机输出指定的功率，并输入给飞行器动力学模型，解算出燃油消耗量，从而初步得到整机重量。

根据飞行器发动机仿真模块输入发动机扭矩等需求，输出发动机实际运行功率，发动机效率及发动机油耗。

根据文献[11]得到的飞行器油箱油面角变化对燃油重心的影响规律：

(5)

燃油X向的重心位置为：

(6)

其中，s为油箱长度；t为油箱宽度；h为油箱高度；油箱油面角α为：当飞行器以俯仰角为θ、航向加速度为a做准定常飞行时α=θ+arctan(a/g)；

结合飞行器燃油消耗仿真结果得到飞行器受燃油消耗产生的重心变化。

图7 飞行器燃油消耗仿真结果

3.2 基于角加速度估计补偿的鲁棒控制方法

根据3.1中所述影响飞行器重心变化因素，开展横列式直升机操稳特性分析及配平与耦合运动规律研究。

在地面牵连坐标系中构建横列式直升机悬停动力学方程：

(7)

随着重心的变化，机身发生倾斜，同时在机身倾斜状况下横列式直升机的配平还会受到强侧风条件影响。其中，横列式直升机所受主要力和力矩如图9所示。

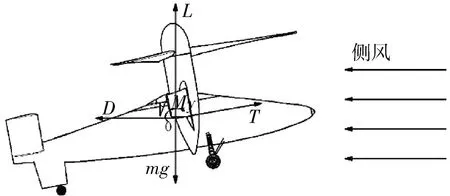
图8 强侧风悬停状态尾坐式飞行器纵向受力示意图

为提高飞行控制系统的鲁棒性和抵抗内、外部扰动影响的能力。本文拟采用角加速度估计信息对外界扰动进行补偿，从而获得强鲁棒闭环性能。

在重心变化过程中，重心变化量及机身倾斜受到侧风对飞行器的影响,最终以力和力矩的方式进行相互作用。同时，加速度信号和角加速度信号是力与力矩在目标物体作用效果的直接体现。通过采用加速度和角加速度信号反馈控制的方法，可以快速地在系统最内环消除模型不确定和内、外部扰动对飞行器运动状态造成的影响，显著地提高飞行控制系统鲁棒性。

然而在实际运作中，系统很难得到高品质的角加速度信号，本文利用横列式直升机的动力学模型和状态测量值角加速度信号，提出了一种角加速度信号估计方法。根据飞行器动力学方程，飞行器俯仰运动的角加速度信号可通过飞行器运动状态和所受内、外部作用力矩计算得到：

(8)

(9)

(10)

上述方法是一种基于飞行器动力学模型的理论计算方法，虽然无法避免模型不确定性和系统扰动问题，但它的动态响应性能及中频和高频特性较好；

角速率传感器采用的直接微分方法虽然存在放大噪声，致使信号品质变差的问题，但是由于微分法无需建立和使用目标的动力学模型和物理参数，其预估结果的真实性很高，可以有效地反映出实际系统中信号的变化，避免了因内、外部扰动和模型不确定性问题导致的偏差，具有良好的准确度和较高的鲁棒性。与模型预测法相反，由于实际系统运行时的信号大多处于低频段，因此微分法估计结果低频特性很好但是由于受到噪声和相位滞后问题的干扰，中频和高频特性较差。

通过互补滤波器将上述模型预测法和微分法得到的估计结果数据进行融合，得到兼具良好动态响应、高品质、高准确度的角加速度信号。同时利用加速度信号和角加速度信号在控制器中进行鲁棒补偿，消除内、外扰动及建模误差的影响。

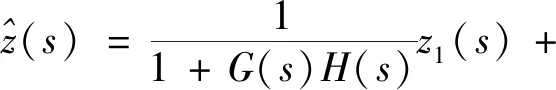
(11)

图9 基于互补滤波器的角加速度信号估计方法

若将H(s)设计为一阶低通滤波器的形式，如式(12)所示，则上述结果将变为式(13)。

H(s)=b/s+a

(12)

(13)

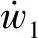
以wn=5Hz，ξ=1为例，画出Bode图如图11所示。由图可知，二者在幅频特性上具有较好的互补性，很好地体现了利用互补滤波器进行数据融合的特点，两者均将各自有利的部分保留至最终的估计结果中，用于补偿对方不利的部分。

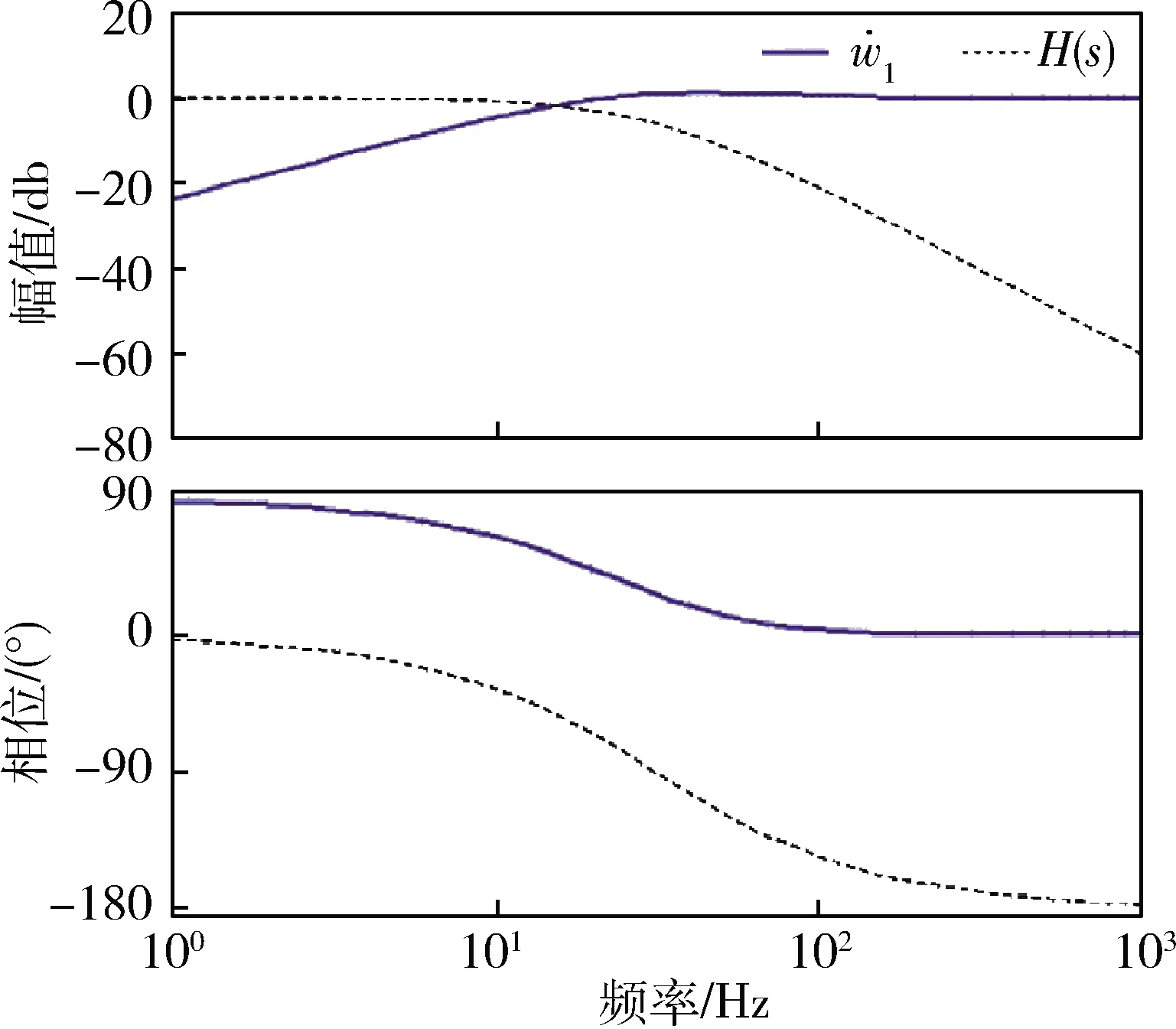
图10 互补滤波器的Bode图

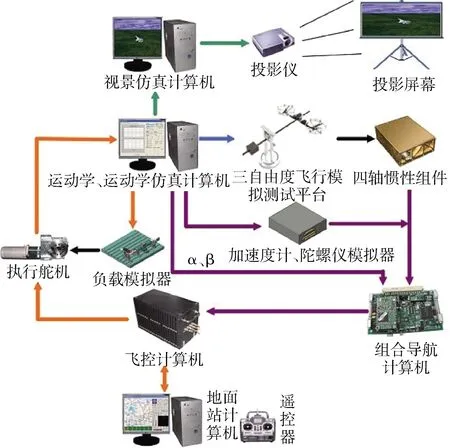
图11 半实物仿真系统总体架构图

4 大闭环半物理仿真

飞行动力学仿真计算机分别通过VIMPCI-5565反射内存实时网卡将飞行器角速度和姿态角传给三自由度飞行模拟测试平台，飞行控制系统随平台一起运动，飞行控制系统通过内置传感器测量平台运动信息，驱动平台系统产生控制力/力矩，通过平台跟踪期望指令，其后经航姿解算算法实时获取横列式直升机姿态角及航向。将机体轴三自由度角加速度解算值传给加速度模拟器，机体速度、位置传给GPS模拟器，然后将飞行器的飞行参数和导航信息传给飞行控制计算机。飞控计算机根据当前飞行任务指令和飞行器当前状态计算得出控制信号。在仿真过程中，可根据需要，通过地面控制站实时控制飞行器。

图12 三自由度飞行模拟测试平台实物图

图13 有无重心变化姿态角指令跟随曲线

5 结论

针对横列式直升机特点，建立了其纵向动力学模型。基于此模型，对横列式直升机进行配平分析。在分析过程中，为求解非线性方程最小值并解决局部收敛算法局部奇异性的问题，采取了基于同伦连续原理修改的Nelder-Mead Simplex优化算法，根据计算结果对比，修改后的算法计算效率。通过优化后的算法求解得到了横列式直升机在不同工况下的配平条件。

为更真实模拟小扰动因素对横列式直升机重心的影响，针对横列式直升机进行了动力推进系统效率模型的建模和仿真，得到飞行中燃油面变化对飞行器重心的影响规律。以此开发了一种基于角加速度估计补偿的强鲁棒控制方法。根据进行的大闭环半实物仿真试验结果表明，本文提出基于角加速度估计补偿的强鲁棒控制方法是有效、可行的。