基于有序分拆的二值自相关序列的设计方法研究*

马天宇，苏建春，杨 静

(广西民族大学a.人工智能学院；b.数学与物理学院，广西 南宁 530006)

0 引言

Hadamard最大行列式问题最早由J.Hadamard在其1893年的论文中提出.[1]它旨在寻找元素为-1/+1的N×N阶方阵，使其行列式的绝对值达到最大.该问题在过去一个多世纪中得到了广泛研究，但至今仍未被完全解决.在组合设计中，人们常常用二值型-1/+1的互补差集(Supplementary Difference Set，简称SDS)构建二值向量和相应的循环矩阵，从而得到Hadamard最大行列式问题在某些特定条件下的解.[2]

利用二值型SDS求解Hadamard最大行列式问题的核心是计算循环矩阵的核，即对应的二值型SDS.令其为矩阵的第一个行向量，则第i个行向量可以通过将第(i-1)个行向量向右平移一位得到.矩阵的核如果通过穷举法进行搜索，则复杂度会随矩阵阶数N的增加呈指数级增长.因此，计算二值型SDS的典型策略是根据二值型SDS需满足的约束条件分析得到序列的若干性质，再根据这些性质逐步压缩搜索空间，在有限的时间内求得符合要求的二值序列.在文献[3]中，Kotsireas等人发现二值型SDS进行压缩后，所得序列的PSD互补性质，从而提出了基于序列压缩方法的组合设计算法.他们还基于群运算中的轨道方法提出了一些特殊二值型SDS的构造方法.近年来，Kotsireas和杨静等人提出了二值型序列的游程编码方法，发现了二值型SDS的若干组合性质，并用于有效地构造求解组合设计中出现的特定类型的多项式方程组.[4-5]

本文采用的二值型SDS是广义Legendre对，而构造出的循环矩阵为广义Legendre循环矩阵.由广义Legendre对求解Hadamard最大行列式问题的其主要思路可以描述如下：

1)设a=(a0，a1，…，an-1)，b=(b0，b1，…，bn-1)为两个长度为n的二值序列，求解方程组

将满足条件(1)的a和b称为长度为n的广义Legendre序列对.

2)分别以a和b为核构造两个循环矩阵A和B.

3)构造如下形式的矩阵.

则所求出的矩阵即为2n+2阶的Hadamard矩阵.

本文采用二值序列的游程编码方式，将(1)的求解问题转化为正整数n的有序拆分问题.这种编码方式能够有效地去除解空间中等价的冗余序列，从而可以极大地减少计算量，提高计算效率，计算得到非等价的广义Legendre对.

1 设计方法的理论基础

1.1 周期自相关函数

设x为长度为n的有限序列，则定义x的第k个周期自相关函数(Periodic Autocorrelation Function，简称PAF)为

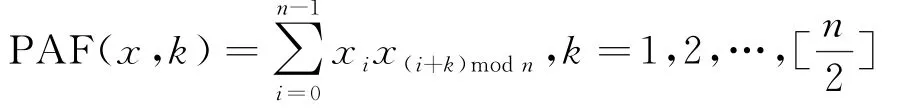
性质1设a=(a0，a1，…，an-1)为长度为n的二值序列，则PAF(A，k)≡n mod 4，其中k=1，2，…，n-1.[6]

性质2如果x′可以通过对x做旋转或逆向旋转得到，则PAF(x，k)=PAF(x′，k)，

证明：

1)设x=(x0，x1，…，xn-1)，x′=(xm，xm+1，…，x(m+p-1)modn)，则x′i=x(x+m)modn且

2)设x=(x0，x1，…，xn-1)，x′=(xn-1，xn-2，…，x0)，则=x(n-1-i)modn，且

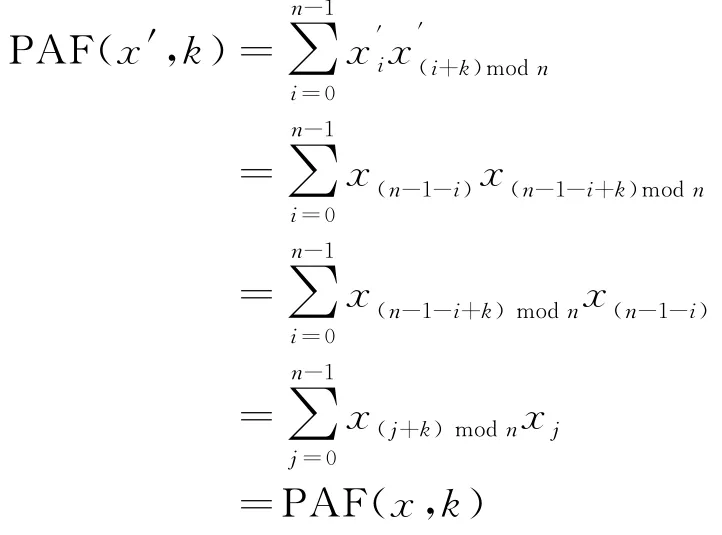
3)设x=(x0，x1，…，xn-1)，x′=(xi，xi-1，…，x(i-n+1)modn)，则x″=(xn-1，xn-2，…，x0)

由(1)，PAF(x′，k)=PAF(x″，k)

由(2)，PAF(x″，k)=PAF(x，k)

因此，PAF(x，k)=PAF(x′，k)，证毕.

由性质2可知，在序列经过旋转或逆向旋转后其PAF值保持不变.若x′可以通过对做旋转或逆向旋转得到，我们称x和x′为等价序列.易知，如果x，y为引用(1)的解，且x′和y′分别为x和y的等价序列，则x′，y′也为(1)的解.因此，不失一般性，我们假设下文出现的二值序列x均以+1开始，-1结束.

1.2 游程与有序拆分

本文采用游程的概念来描述一个-1/+1的二值序列.设x为一个-1/+1的二值序列，则x的一个游程定义为该序列满足下列条件的一个片段：

1)其元素只含+1或只含-1；

2)相邻的片段中都具有相反的符号.

例如，给定a=(1，1，-1，1，1，-1，-1)，则a中有4个游程，即(1，1)，(-1)，(1，1)，(-1，-1).由于每个游程中元素均为+1或-1，因此我们可以将游程的信息表示为游程的长度.例如，上述序列x的游程可以表示为2，1，2，2.这样我们就将一个-1/+1的二值序列重新编码为正整数n的一个有序偶拆分.例如，给定a=(1，1，-1，1，-1，1，-1，-1，-1)，则a可以编码为一个9的偶拆分为(2，1，1，1，1，3)；反之，如果给定一个9的偶拆分(2，1，1，1，1，3)，则可将其解码得到一个长度为9的二值序列(1，1，-1，1，-1，1，-1，-1，-1).这两个过程分别称为二值序列的编码和解码.

性质3设a为长度为n的二值序列，#run(a)表示a的游程数，#1-run(a)表示a中长度为1的游程数，则

1.3 广义Legendre对的组合性质

定理1设a和b为满足(1)的广义Legendre序列对，游程数量分别为#run(a)和#run(b)，“1”游程数量分别为#1-run(a)和#1-run(b).则

1)#run(a)与#run(b)为偶数；

2)#run(a)+#run(b)=n+1；

本文提出的设计方法的基本思想是将寻找二值序列x的问题转化为寻找满足特定条件的游程的问题.而该问题又等价于寻找n的一个有序偶拆分(即n=n1+n2+n3+…+ni，ni>1，i=1，2，…，t).我们利用广义Legendre序列对编码后的偶拆分信息，将序列的穷举搜索问题简化为正整数的有序偶拆分问题.计算结果表明，这些信息可以极大地缩小压缩空间，解决规模较大的组合设计问题.

1.4 PSD检测

PSD检测在组合设计中常常被用于筛除不符合要求的广义Legendre对.下面我们给出PSD的定义.给定一个长度为n的复序列x=(x0，x1，…，xn-1)，令ω=e2π/n表示n次本原单位根.则x的离散傅里叶变换(Discrete Fourier Transformation，以下简称“DFT”)定义为：

而x的第k个PSD值为

PSD(x，k)=|DFT(x，k)|2=DFT(x，k)·

定理2若a和b是一组广义Legendre对，则序列a和b的PSD值满足如下关系：

PSD(a，k)+PSD(b，k)=2n+2(1≤k≤n-1)

因为PSD的值大于等于0，因而PSD(a，k)≤2n+2.我们通常用广义Legendre对的这个性质来对其进行PSD检测，从而过滤掉不必要的序列，有效地减少计算量.

2 实验结果

我们基于上述理论，用C语言实现了一种新的寻找广义Legendre对的组合设计方法.该方法可以有效地去除等价或冗余的序列，从而计算得到具有较大规模的广义Legendre对.本节中我们列出了采用该方法计算出的若干广义Legendre对.

2.1 长度为35的PAF序列

当n=35时，我们找到3833对符合条件的广义Legendre序列对，以下仅列出其中一例.

a对应的有序拆分为(1，1，1，1，1，2，2，2，5，1，1，2，1，1，4，2，2，5)

b对应的有序拆分为(1，1，1，1，2，2，4，3，2，1，2，1，1，1，3，1，2，6)

解码后的a序列为

(+-+-+--++--+++++-+--+-++++--++-----)

解码后的b序列为

(+-+-++--++++---++-++-+-+++-++------)

a的PAF序列为 (-1，-1，-1，-1，-1，-1，-1，-1，-1，-1，3，-1，3，-13，-1)

b的PAF序列为 (-1，-1，-1，-1，-1，-1，-1，-1，-1，-1，-5，-1，-5，-1，-5，11，-1)

2.2 长度为41的PAF序列

当n=41时，我们找到3807对符合条件的广义Legendre序列对，以下仅列出其中一例.

a对应的有序拆分为(1，1，1，1，1，2，2，2，1，1，1，2，1，5，5，1，6，3，2，2)

b对应的有序拆分为(1，1，1，1，1，1，2，1，3，2，3，4，2，1，2，1，1，5，3，1，2，2)

解码后的a序列为(+-+-+--++--+-+--+-----+++++-++++++---++--)

解码后的b序列为(+-+-+-++-+++--+++----++-++-+-----+++-++--)

a的PAF序列为(1，1，1，1，1，1，1，1，1，-11，-3，-3，-7，-7，5，1，1，-7，1，1)

b的PAF序列为(-3，-3，-3，-3，-3，-3，-3，-3，-3，9，1，1，5，5，-7，-3，-3，5，-3，-3)

2.3 长度为49的PAF序列

当n=49时，我们找到70对符合条件的广义Legendre序列对，以下仅列出其中一例.

a对应的有序拆分为(1，1，1，1，1，1，4，1，2，1，2，5，2，2，1，3，3，2，1，2，1，5，5)

b对应的有序拆分为(1，1，1，1，1，1，1，4，2，1，4，3，2，4，1，4，2，1，2，2，3，1，2)

解码后的a序列为

(+-+-+-+----+--+--+++++--++-+++---++-++-+++++-----)

解码后的b序列为

(+-+-+-+--+-++++--+----+++--++++-++++--+--++---+--)

a的PAF序列为

(1，1，1，1，-11，1，1，1，1，1，-11，1，1，5，5，1，-3，-3，-3，-7，-7，1，1，-3)

b的PAF序列为

(-3，-3，-3，-3，9，-3，-3，-3，-3，-3，9，-3，-3，-7，-7，-3，1，1，1，5，5，-3，-3，1)

3 结论

本文通过对广义Legendre对的组合性质进行研究，将二值序列的搜索问题转化为正整数的有序拆分问题，提出了一种新的二值自相关序列的设计方法.实验结果表明：该方法可以有效地缩小搜索空间，去除不必要的冗余序列和等价序列，从而提高计算效率.由于该方法具有良好的并行性质，今后可以通过MPI编程将其部署到多核服务器或大型计算集群，用以求解大规模的公开问题.此外，本文提出的算法也可借鉴到其他二值SDS序列、三值SDS序列的设计方法中，并与现有的设计方法相结合，求解类似的组合设计问题.