基于路径搜索的交通拥堵判别研究

陈 智，孙德辉

(北方工业大学城市道路交通智能控制技术北京市重点实验室，北京 100144)

0 引言

城市中越来越明显的交通拥堵现象制约着当今社会的发展伴随着科技的进步，GPS设备大范围的应用在私家车上，尤其是出租车. 结合浮动车GPS数据处理、挖掘、分析车辆运行的时空关联关系，能有效并快速研判道路交通拥塞状态，从而对交通拥堵起缓解作用.

Mennis J等[1]根据空间网格相关性规则，将空间矢量区分为具有同样面积的网格，并详细研究了网格之间的时间-空间相关性. 该方法可以有效的解决时空约束问题，但因为没有明确的提出对网格规则划分的标准，致使仍有不足之处. Florian Verhein等[2]基于车辆时间-空间位置，对空间谓词进行描述，将拥堵高峰区域进行简化，同时探索车辆在时间-空间中的移动相关性，进而找到了其移动的规律.

岳慧颖[3]通过空间约束深度挖掘时空序列中的空间关联项，添加时间约束条件，并获取时间—空间的关联项，基于此获得对象之间的时间和空间的关联规则. 在数据提取时分别挖掘时间和空间数据. 这有利于对时空相关性规律的挖掘，而且不对结果产生影响，然而在一定程度上加大了算法的计算过程，扩大了数据的存储量.

丁铁成[4]提出“road to vector”方法，以时间轴、投影、地图等多个视图为基础，搭建了道路相关性的可视化分析系统平台，可以使用户在多尺度、多角度下对轨迹数据进行分析，从中提取道路之间的相关性.

张婧[5]描述了道路交通流在区域路网拥堵中存在的时间-空间分布特性，设计了时空相关性指标和计算方法，提出了基于交通流时空关联性的拥堵区域研判方法，有效应用于邻近道路的实时拥堵预警.

李光强等[6]在现有研究中，将事件影响域作为条件，划分时间—空间域，同时引入了一个关系谓词来构建时空域和事件之间的关系，利用一种新方法在路段上进行数据挖掘，从而提高挖掘的效率.

乔春凯等[7]提出了一种时序关联规则挖掘方法，基于智能算法划分序列流时间和空间的关联特征，实时预测道路网络的拥堵状态，达到在复杂交通环境下拥堵预测的准确度提高的目的.

刘端阳等[8]提出Ncut的交通子区划分方法，基于交通流量和路段速度信息计算交通态势，结合交叉口间距离获得动静态结合的关联度指标，应用Ncut划分算法对道路网络进行分类，调整子区边界上的交叉口使得子区总关联度达到最大，同时使子区内部的交叉口交通态势更为相似.

丁恒等[9]通过比例积分控制外部道路网络的交通累积量，将实际交通的流出率与宏观基本图曲线相关联的期望流出率的差值作为特征变量，建立可拓集合，路网入口边界PI反馈控制量通过内部可拓提升控制器进行调节，控制了驶入路网的交通流以避免交通拥堵.

通过分析上述的国内外研究可知，多数研究聚焦于分割了时间和空间两者的关联性分析，缺乏构建基于时空维度的关联模型研究，造成了一定的局限性. 而在区域交通拥堵状态的研判方面中，时空关联性方法应用鲜有涉及. 因此，本文以出租车GPS数据为基础，引进差异聚合系数，该系数由Pearson和Kendall相关系数组成，并搜索区域道路网络中的高相关路径. 结合莫兰象限构建了基于时空关联分析的道路网络拥堵区域研判方法，进一步利用海南市出租车GPS数据进行案例分析.

1 基于差异聚合系数的高相关路径搜索

实测的GPS交通数据是指通过不间断的观察城市路网中互相关联的道路段形成的时间序列，即交通流时间-空间数据. 这些交通流数据来源于出租车实时采集，可以真实、准确地反映城市交通的运行特点.

相关性分析定义为分析2个或多个有序向量之间的多维特征变化相关性，Pearson相关系数描述的是2个向量的协方差和标准差的乘积之比，分类变量间的相关性程度用Kendall相关系数来描述，以τ表示值. 本文基于现有的2种相关度分析方法，构造新指标.

时间-空间相关性分析可以应用于一条道路随时间-空间变化的交通流相关性，也可以应用于路网随时间-空间变化的交通流相关性. 以往的研究只要集中于用道路聚类对交通区域进行划定，但是，传统的道路聚类在划分道路时没有统一的标准，在交通拥堵区域判别应用时取得效果小. 本文基于高相关路径动态划分道路网络的拥堵区域，由于道路交通存在随机性，它们之间的相关性也会随之变化，因此只用历史数据对路径进行划分，存在时效性和片面性.

当道路发生拥堵时，空间-时间也会随之发生变化，但依然存在相关性. 在城市路网中迭代计算2条以上路网的相关性，研究路网间的交通流状态时间-空间特性变化过程.

将高相关路径的搜索与判定过程进行约简化，并根据融合相关系数(即Kendall和Pearson相关系数)之间的关联性，创建一种新的指标. 将路段链集合F中上下游每两条路段间关联度异质与全局道路网络关联度异质之间的比率定义为相关性差异聚合系数，如果路段链集合F中的道路相关度差异性越小，则表现为差异聚合系数越低，若为高相关路径，则表现为内部关联性越高. 差异聚合系数见式(1)～(3)：

(1)

(2)

(3)

利用定义的相关性聚合度，通过图1的步骤对高相关性路径进行搜索.

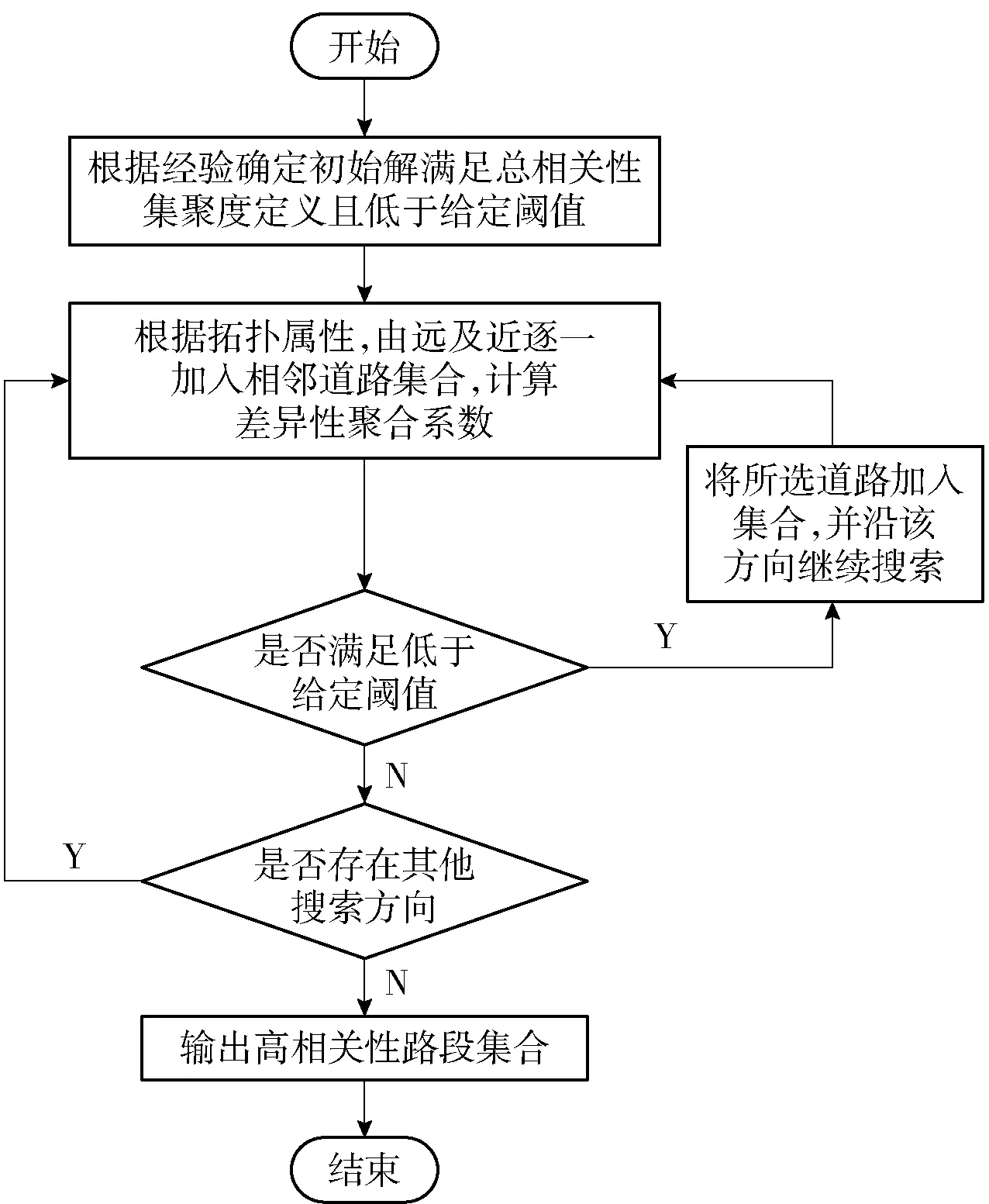
图1 高相关路径搜索方法流程

2 莫兰象限

韦伟基于空间自相关理论，在传统莫兰时空指数中添加了时间维度这一指标，构建出新Moran’s I方法[10]，可以对路网的交通时空状态进行分析. 本文以海南海口市的火车北站周围共105条路段为例，研究GPS数据，分析路网交堵状态的时间-空间变化特性. 采用前文提出的高相关路径搜索算法，提取高相关路径，对短时路网交通拥堵状态进行判别.

为了能直观体现时空各元素之间的异向特性和聚合特性，引入空莫兰散点图，散点图横轴归一化属性值X(p, i)，该值源于时空元素ST(p, i )；纵轴为经过归一化后的时空属性加权值YX(p, i)(记为时空滞后值，正值表示时间元素聚合，负值则为异向)，该值临近时空范围内连接时空元素.

在散点图中寻找时空元素所处的象限，得出时空元素对应的时空特性：

第Ⅰ象限：X(p,i)>0,YX(p,i)>0，该象限点的时间和空间特征表征为高值聚合状态(HH)，即时空元素及其相邻区域范围内的元素本身属性值都比较高.

第Ⅱ象限：X(p,i)<0,YX(p,i)>0，该象限点的时间和空间特征表征为低值异向状态(LH)，即低值的时空元素被包含于其相邻区域范围内属性值较高的元素.

第Ⅲ象限：X(p,i)<0,YX(p,i)<0，该象限点的时间和空间特征表征为高值扩散(LL)，即时空元素及其相邻区域范围内的元素本身属性值都比较低.

第Ⅳ象限：X(p,i)>0,YX(p,i)<0，该象限点的时间和空间特征表征为高值异向状态(HL)，即高值的时空元素被包含于其相邻区域范围内属性值较低的元素.

综上分析，第Ⅰ和Ⅲ象限的时空元素全都拥有聚合性的特征，而第Ⅱ和Ⅳ象限的时空元素均拥有异质性的特点. 也就是当时间和空间融合的元素表现为共同特征时，体现出聚合性；而当其表现为不同的特性时，则体现出异质性.

3 路网拥堵控制区域判别

根据以上所述道路时空状态划分，在城市路网中，可将道路按照所处莫兰象限进行4类状态的划分：处于莫兰第Ⅰ象限即HH的畅通聚合路段，为路网拥堵中的保障路段，保障路段往往道路状况良好，具有较高的道路通行能力，一般不易发生拥堵，或短暂拥堵后迅速消散，可容纳数量较大的上游拥堵车辆驶入，并保障交通流行驶水平；处于莫兰第Ⅱ象限即LH的畅通异向路段，为路网拥堵中的预警路段，先于周边路段出现拥堵，滞后于周边路段畅通；处于莫兰第Ⅲ象限即LL的拥堵聚集路段，为路网中的拥堵产生路段，往往为拥堵产生点以及扩散点，拥堵从该类路段产生并向周边扩散；处于莫兰第Ⅳ象限即HL的拥堵异向路段，为路网中的拥堵疏导路段，往往为拥堵消散点，滞后于周边路段拥堵，先于周边路段畅通，往往作为车辆由拥堵聚合路段驶入畅通聚合路段的通道.

基于以上对于道路交通流拥堵相关性分析，可通过时空莫兰散点图选取拥堵聚合路段(LL)作为起点，根据前文所述方法快速并准确搜索出高相关性路径.

通过高相关路径中相关路段所处莫兰象限所代表的交通流拥堵时空特性，进行拥堵区域交叉口补充，从而对路网拥堵控制区域进行判别.

拥堵区域判别步骤如下：

步骤1选取路网中处于莫兰第Ⅰ象限LL状态的路段为起始路段l1，其上、下游交叉口分别设为c1,c2；

步骤2以l1为起点，进行基于差异聚合系数的高相关路径搜索，搜索得到以l1为起点的高相关性路径l2,l3…ln，其中l2的上游交叉口即为c2，下游交叉口为c3，同理，剩余的相关路径下游交叉口将设置成c4…cn+1；

图2 路段处于莫兰第Ⅰ象限时拥堵区域交叉口的筛选

步骤3根据相关路径中各路段所处莫兰象限，按路径顺序进行交叉口筛选补充与剔除. 共计4种路段情况：①若路段处于莫兰第Ⅰ象限，即HH畅通聚合状态，则将该路段上下游交叉口从拥堵控制区域中去除，并将高相关性路径由此进行分割，如图2所示，实线框中为拥堵控制区域交叉口；②如路段处于莫兰第Ⅱ象限，即LH畅通异向状态，则保留该路段上下游交叉口，如图3所示实线框中为拥堵控制区域交叉口；③如路段处于莫兰第Ⅲ象象限，即LL拥堵聚合状态，则保留该路段上下游交叉口，且将该路段所有相连交叉口划分为拥堵控制区域，如图4所示实线框中为拥堵控制区域交叉口；④如路段处于莫兰第Ⅳ象限，即HL拥堵异向状态，则仅保留该路段上游交叉口，将下游交叉口从拥堵控制区域中去除，并将高相关性路径由此进行分割，如图5所示实线框中为拥堵控制区域交叉口；

图3 路段处于莫兰第Ⅱ象限时拥堵区域交叉口的筛选

图4 路段处于莫兰第Ⅲ象限时拥堵区域交叉口的筛选

图5 路段处于莫兰第Ⅳ象限时拥堵区域交叉口的筛选

步骤4若出现由于LL或LH路段保留交叉口与HH或HL路段剔除交叉口发生冲突时，对交叉口进行保留；

步骤5依次筛选高相关路径中所有交叉口至交叉口cn+1结束，根据筛选结果即为拥堵控制区域A，包含所有保留交叉口. 实际判别流程见图6.

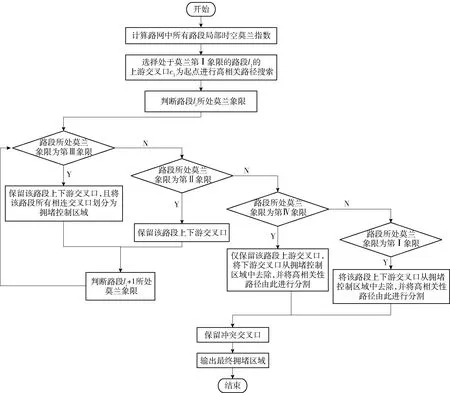
图6 路网拥堵控制区域判别流程

4 实例验证

以自2016-11-01—12-31期间的海南海口市政府周边共计105条路段3 000多辆出租车产生的GPS数据为研究对象，提取道路拓扑结构：

图7 实际道路网络的拓扑结构图

以2016-11-03，13：00-14：00数据为基础，通过计算路网中路段局部时空莫兰指数，选取莫兰象限为第Ⅲ象限的海口市政府周边长滨东四街西向东方向作为起始路段进行高相关性路径搜索. 获得高相关性路径l1-l7.

图8 高相关路径搜索示例

计算城市路径中所有路段在莫兰象限的所属位置.

图9 城市路段所处莫兰象限计算示例

根据前文所述拥堵区域判别步骤进行交叉口筛选，确定拥堵控制区域. 图10中方框所表示交叉口为拥堵控制交叉口，其中由于c6交叉口下游南侧交叉口为高架桥，故不纳入拥堵控制区域. 蓝色圆框即为剔除交叉口. 虚线部分即为拥堵控制区域.

图10 拥堵控制区域判别示例

5 结论

以出租车的GPS数据为研究对象，在已有的通过Pearson系数进行的交通拥堵时空特性研究基础上，通过引入Kendall相关系数弥补Pearson系数针对道路网络拥堵状态研判的不足. 引进差异聚合系数，该系数由Pearson和Kendall相关系数组成，并搜索区域道路网络中的高相关路径. 将时间维度约束条件添加到莫兰指数，构建出时空的莫兰象限，分析了城市路网中交通流的时间-空间聚合消散相关性. 提出了基于高相关度路径搜索的拥堵区域研判方法. 计算路网中所有路段局部时空莫兰指数，选择处于莫兰第Ⅰ象限的路段的上游交叉口为起点进行高相关路径搜索，依次判断路段所处的莫兰象限，输出拥堵区域. 最后，采用海口市长滨4路实例数据进行实例验证，证明了该方法判别的效果，且具备大数据应用的前景.