基于CFD和FSI的摆线泵仿真分析
2020-07-15黄龙龙王艳华徐劲松
黄龙龙,王艳华,刘 勇,,徐劲松
(1.中北大学 能源动力工程学院,山西 太原 030051;2.中国兵器工业内蒙古第一机械制造(集团)有限公司,内蒙古自治区 包头 014030)
引言
摆线内啮合齿轮泵结构紧凑、体积小、转速高,且具有运动平稳、噪声低、容积效率较高的特点,适用于燃油系统中的传输、加压、喷射的燃油泵以及航空航天、车辆等绝大多数工程领域的润滑泵.国内外学者在几何学、运动学与动力学特性和数值仿真等方面开展了大量研究工作。在摆线齿廓方面,SAEGUSA Y等[1]介绍了摆线机油泵转子齿廓的形成。FABIANI M等[2]采用微积分方法定量计算齿间容积,并对配流盘几何参数进行了设计计算。徐学忠[3-4]、LIU H等[5]应用复数矢量方法,推导出摆线泵内转子的齿廓曲线方程。HWANG YW等[6]提出了提高泵效率的数学模型,推导了不产生根切的条件。在CFD仿真方面,陆钧成等[7]基于CFD对水泵进行优化。徐刚[8]建立了摆线泵模型并对其进行数值模拟。RUNDO M[9]对机油泵进行流体动力学仿真,研究不同转速下泵的性能。FROSINA E等[10]使用PumpLinx对Aprilia公司的一种高性能摩托车发动机的油泵进行仿真分析。KUMAR M S 等[11-12]分析了无污染油在室温和高温下模拟了转子转速、流体黏度、流道数等重要参数对泵流量的影响。王铮等[13]分析了发动机供油系统压力脉动。为了提高仿真的真实性,GAMEZ-MONTERO P J等[14]和CASTILLA R等[15]采用接触点黏度模型模拟齿轮之间的固-固接触。大多学者采用CFD方法研究摆线泵不同结构、不同工况等下泵的性能,未考虑FSI方法对仿真结果的影响。在流固耦合研究方面,RUGONYI S等[16]用COMSOL多物理方法研究蠕动泵的流体结构相互作用。TAKASHI N等[17]和SARRATE J等[18]采用任意拉格朗日-欧拉方法,将刚体与流体的界面条件结合起来,描述了流体与刚体在平移和旋转运动下的运动方程。以上学者采用流固耦合方法分析,并描述了流固耦合原理和对仿真结果的影响。
目前在摆线泵数值模拟方面,多数研究基于CFD对不同运行工况(如转速、温度等)下的泵进行分析,未考虑在流固耦合作用下泵的特性。首先基于COMSOL建立了摆线泵的模型,对流固耦合界面进行设置,设置相应的边界条件后对泵进行CFD和FSI仿真,在流量和压力特性方面与试验结果进行对比,并将CFD和流固耦合进行详细分析,得出更接近真实的摆线泵分析方法,更有利于对泵的流场和转子动力学特性进行分析。
1 摆线泵模型
1.1 摆线泵模型参数
摆线泵由2个主要部件组成:1个内转子和1个比内转子多1个齿的外转子。内转子中心线与外转子中心线之间的固定偏心距a。当转子旋转时,流体被吸入到旋转油腔中,达到最大容积后随着旋转的继续,腔室容积减小,迫使液体流出腔室。被测试泵的性能如表1所示。

表1 被测试泵的性能
为了与试验进行对比,建立了满足相应性能的模型,表2为摆线泵几何参数的取值。
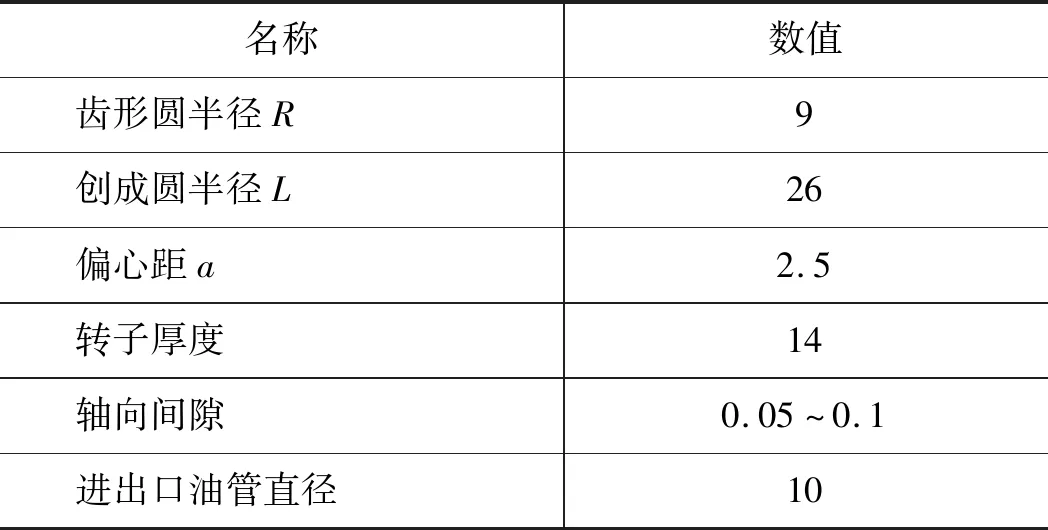
表2 摆线泵几何参数 mm
1.2 搭建摆线泵试验台
1) 试验台搭建思路及操作
试验台构成如下:通过联轴器2将电机1、扭矩仪3、泵轴4连接起来,从而电机带动泵运转的同时可以通过扭矩仪测试转速和扭矩等;将油箱11通过油管与泵的进口进行连接,将泵的出口与油箱连接使得润滑油在运行过程中循环使用;在泵的出口安装压力表5-1和压力变送器6-1,来采集泵出口处的压力,同时在泵出口安装节流阀9比例溢流阀10,来对出口压力进行调节;在节流阀出口处安装压力表5-2和压力变送器6-2测试节流阀出口处压力,同时在节流阀出口处安装涡轮流量计来测试泵出口处流量。
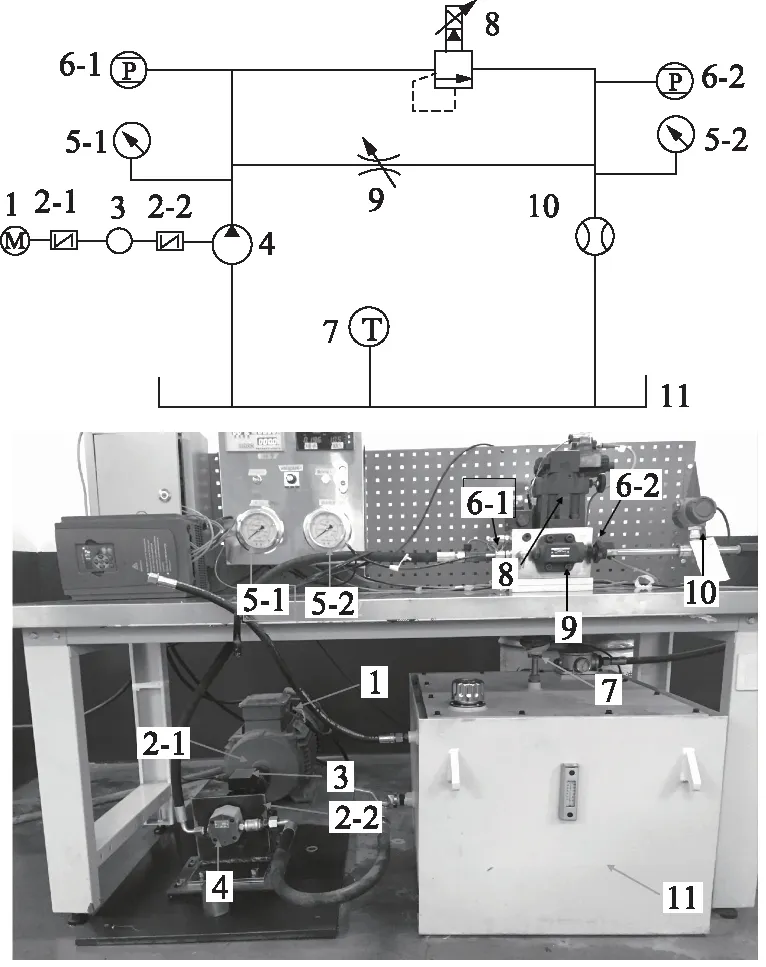
1.变频电机 2.联轴器 3.转矩转速传感器 4.被测试机油泵 5.压力表 6.压力传感器 7.温度传感器 8.溢流阀 9.节流阀 10.流量传感器 11.油箱图1 测试试验台连接图
2) 操作流程
试验过程中基本操作流程:打开节流阀,使出口压力处于低压状态; 启动电机,让泵运转一段时间,在流量、压力、温度稳定以后进行下一步;调节变频器,使通电机转速为指定测试条件下的转速;调节节流阀,改变泵出口压力;观察流量压力特性曲线,并采用LabVIEW进行数据采集。
2 摆线泵数值分析
2.1 摆线泵CFD仿真分析
在对摆线泵进行CFD数值模拟时,需要对流体域进行建模,流体域主要包括内外转子间的旋转区域、轴向泄漏区域、进出油腔和进出油管道,旋转区域和泄漏区域受转子的影响产生运动,其几何形状发生变化;进出油腔和进出油管为静止流体域,详细模型图如图2所示。
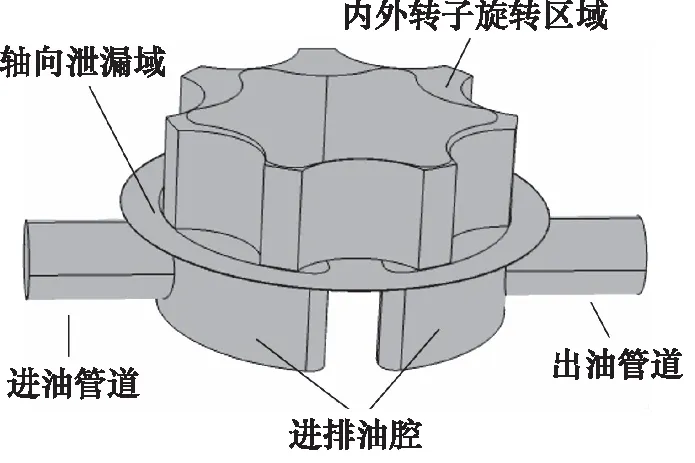
图2 摆线泵流体域模型
1) CFD基本原理
(1) 流体中某一点的非定常三维质量守恒或连续性方程如下:
(1)
(2) 惯性(非加速)参考系中的动量守恒:
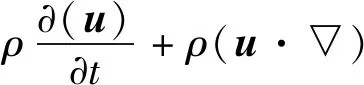
=▽·[-pI+μ(▽u+(▽u)T)]+F
(2)
式中,ρ—— 流体密度,kg/m3
p—— 静态压力,Pa
T—— 流体温度,K
u—— 速度矢量,m/s
F—— 体积力矢量,N/m3
2.2 流固耦合基本原理
在ALE (Arbitrary Lagrange-Euler)公式中,从拉格朗日到欧拉变换,我们可以通过任意指定参考点的速度分布来任意选择描述控制方程。不可压缩流动的动量守恒定律和连续方程在参考描述中表述如下:
(3)
式中,σ—— 应力张量,Pa
uf—— 空间坐标系下材料粒子的速度矢量,m/s

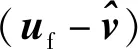
2) 结构运动方程
(4)
式中,ρs—— 材料密度,kg/m3
d—— 结构位移矢量,m
σs—— 二次Piola-Kirchhoff应力,Pa
Fb—— 体积力矢量,N/m3
3) 流固耦合方程
在流体-结构界面上Гf-s,当黏性流体与固体相互作用时,流体-结构界面必须满足平衡和相容条件。这些条件是:
σ×n=σs×n
(5)
在Гf-s上,n是垂直于边界的法向矢量,流体施加在固体边界上的总力等于流体所受反作用力的负数,在Гf-s上流体的运动由固体传递而来,网格节点的速度需要满足连续性条件。
通过FSI的理论分析得出:在耦合界面上, 流体动力及固体的运动事先都不知道, 只有在系统地求解了整个耦合系统后, 才可给出它们的解答, 这正是相互作用的特征所在,也是与CFD的不同之处,若没有这一特征, 其问题将失去耦合作用的性质。
图3为流固耦合仿真时建立的模型,表3为流体和固体的物理参数。
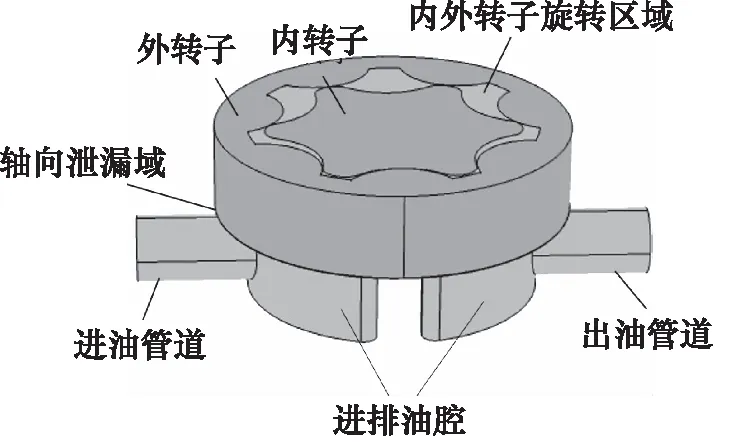
图3 FSI仿真模型
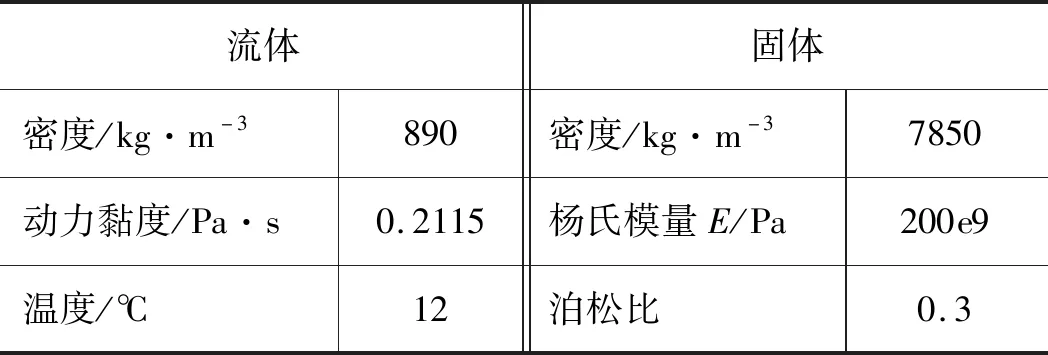
表3 流体和固体基本物理参数
2.3 边界条件设置及网格划分
1) 边界条件设置
(1) 流体区域边界条件
对于流体域具体边界条件设置为进口为当地大气压,出口为0~2.5 MPa,静态区域与动态区域采用一致对,保证数据传递,动态变形域采用ALE动网格方法,具体边界条件设置如表和图所示。对于流固耦合仿真指定内外转子的运动及流体与固体耦合界面,具体设置如图4所示。
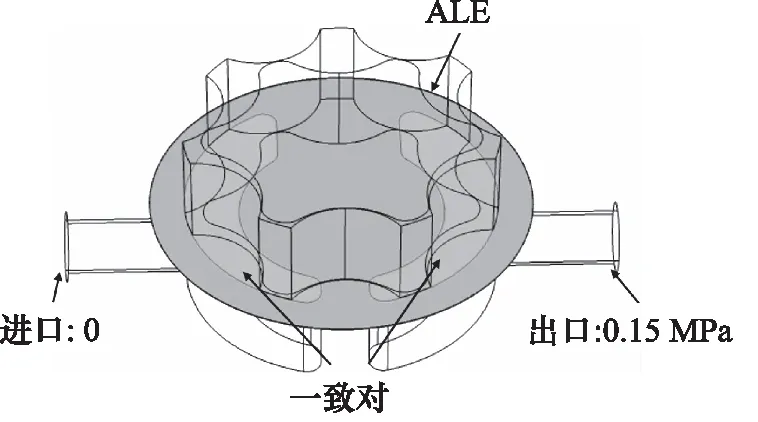
图4 流体域边界条件设置
(2) 流固耦合区域设置
图5为内外转子与之间的流体与耦合界面,在界面处将产生流固耦合作用。
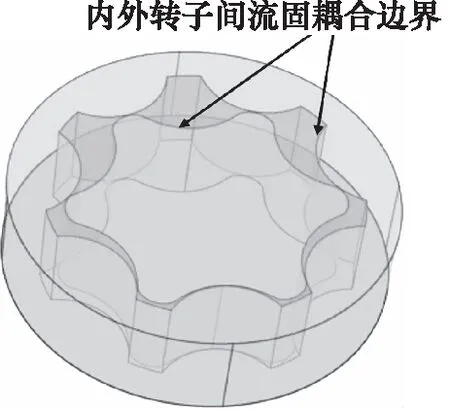
图5 流体与固体耦合界面
2) 网格划分
旋转区域内外转子间存在0.1 mm的间隙,因此应当设置最小网格尺寸为0.01 mm,最大网格尺寸不能过大,对旋转区域和泄漏区域采用扫掠网格,其他静止流体域采用自由四面体网格,具体网格如图6~图8所示。

图6 流体域网格划分
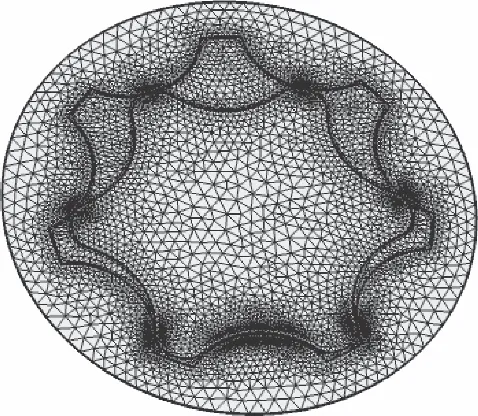
图7 轴向泄漏区域网格划分
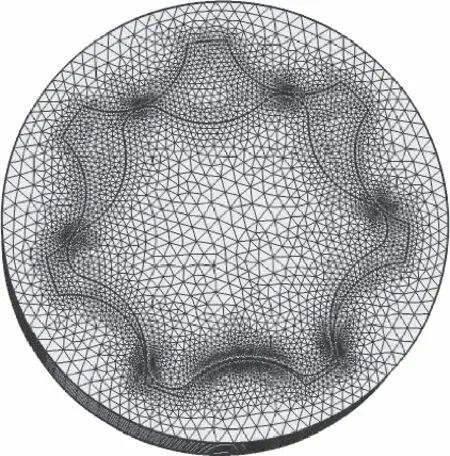
图8 流固耦合转子与旋转流体网格
3 CFD,FSI和试验对比分析
3.1 出口流量和压力特性对比分析
通过分析CFD和FSI仿真出口处的流量和压力特性曲线,并与试验结果进行对比,如图9、图10所示为CFD,FSI和试验的对比。

图9 出口处瞬时流量波动分析
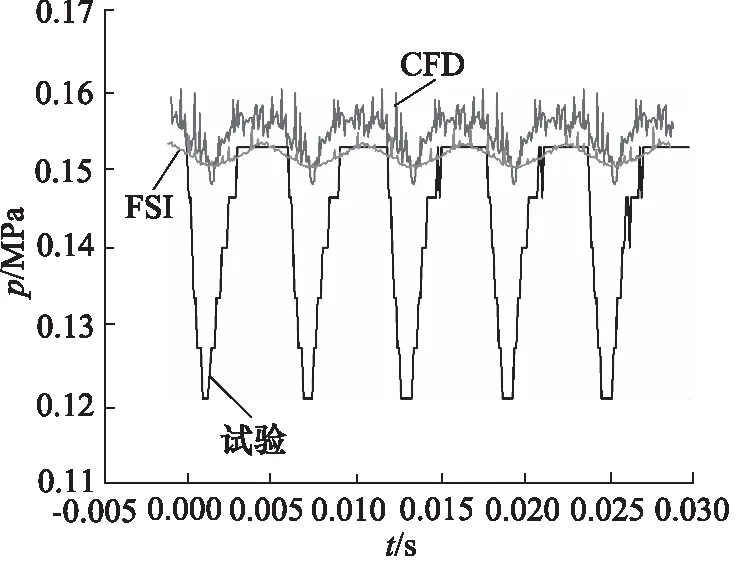
图10 出口处瞬时压力波动
对CFD,FSI和试验的流量、压力的平均值进行分析,式(6)为流量、压力的平均值计算公式,表4和表5为具体的计算结果,并对比了CFD和试验与FSI的误差。
(6)
式中,Qm,pm—— 平均流量,平均压力
Qsh,psh—— 瞬时流量,瞬时压力
δQ,δP—— 流量脉动,压力脉动
通过图9、图10、表4和表5分析,可以得出:
(1) 在流量特性方面:FSI的仿真的流量平均值均高于试验和CFD的结果,更接近于试验值,在CFD计算中,内外转子与流体接触界面,只指定了旋转位移,而转子在旋转过程中将惯性力施加于流体,造成CFD计算结果低于试验值;FSI出口处流量脉动率最大,由于试验中出口采用较长的橡胶管,而且经过了节流阀、溢流阀这些部件,且试验测试存在误差,导致流量波动非常小;
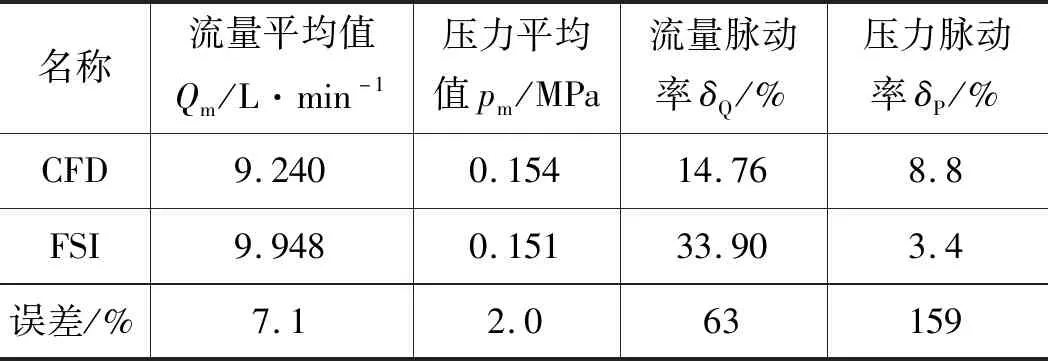
表4 CFD和FSI流量压力特性对比分析
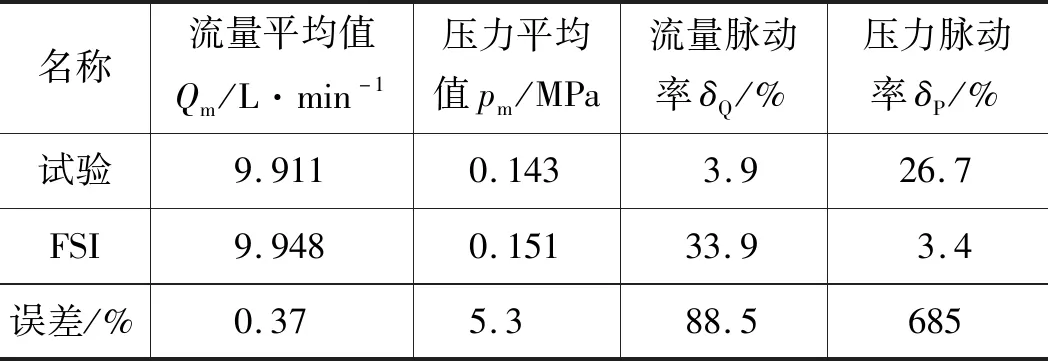
表5 试验和FSI流量压力特性对比分析
(2) 在压力特性方面:FSI和试验的出口压力平均值均低于CFD的仿真值,FSI的压力均值更接近CFD的结果,出口处压力边界条件为0.15 MPa,因此CFD和FSI的结果更合理;对比三者的压力波动情况,CFD和FSI的压力脉动率比较小,由于试验过程中管路复杂且流过节流阀、溢流阀等部件以及压力传感器存在误差,导致试验测试的出口处压力脉动率较大。
综合以上分析得出:由于数值模拟、试验均存在误差,试验、CFD和FSI结果存在差异,在流量方面FSI更接近试验,在压力方面FSI和CFD更符实际情况。结合FSI的理论分析得出:由于泵在运转过程中转子驱动流体运动从而产生流体和固体的相互作用,由于CFD在运动界面上只指定了运动,而FSI在流固耦合界面处流体不仅产生运动,而且受到固体的作用力,耦合对计算结果有很大的影响,因此FSI的仿真更接近实际。
3.2 CFD和FSI对比分析
为了研究耦合对计算结果产生的影响,进一步分析CFD和FSI的差异性,选择CFD和FSI的旋转流体域某截面(Z=7 mm),由于CFD和FSI的流量压力都是周期性波动,选择1个周期来对比CFD和FSI仿真结果,如在0.015~0.022 s间选择6个时间节点,对比压力和速度的分布。如图11和图12分别为截面压力和速度的对比图。

图11 CFD和FSI旋转域某截面速度分布对比分析

图12 CFD和FSI旋转域某截面压力分布对比分析
通过图11和图12中压力、速度云图及最大值最小值分析得出:在吸油区域计算得到的负压CFD大于FSI,计算得到的速度CFD小于FSI;在排油区计算得到的正压力CFD大于FSI,计算得到的速度CFD小于FSI的结果。
进一步对内外转子与流体接触的区域进行对比分析。图13a、图13b分别为内外转子某点处压力随时间的变化情况。
通过图13a和图13b内外转子某点压力变化得出:CFD在内外转子表面上一点处的压力值均大于FSI的压力值,产生这种差异的主要原因是在FSI中由于固体的惯性力作用于流体从而改变了流体的运动状态,流体的速度增大,从而压力减小。
综合以上分析得出:耦合对计算结果有很大的影响,由于CFD在转子流体交界面处指定了位移运动,从而确定了边界处的速度,而流固耦合存在转子与流体的相互作用,由于转子几乎不变形,因此不考虑弹性力的作用,但转子在高速旋转,存在惯性力,通过交界面将惯性力施加于流体,从而改变流体的运动状态,从而增加了流体的速度降低了流体的压力。
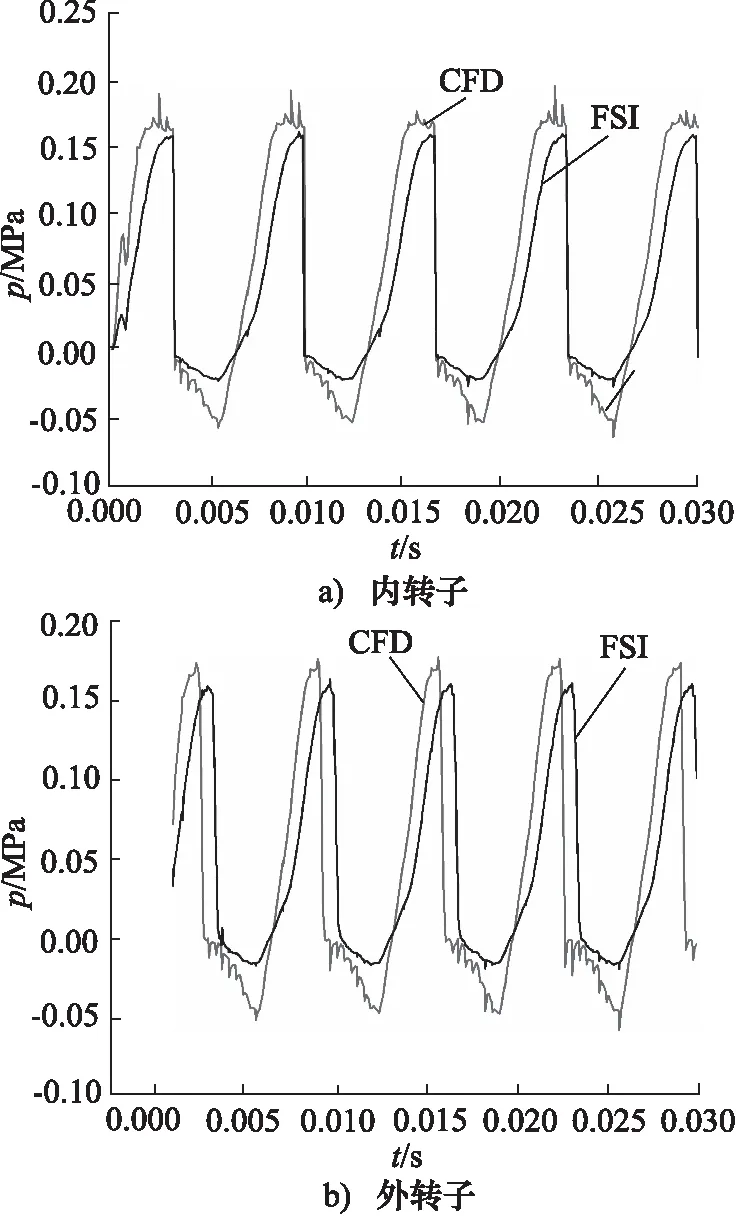
图13 内外转子表面某点的压力分布
4 结论
通过建立摆线泵模型,根据CFD和FSI的基本原理,设置相应的边界条件和划分网格后对摆线泵进行CFD和FSI仿真分析,并于试验结果进行对比,研究结果表明:
(1) 在流量特性方面:FSI的仿真的流量平均值更接近于试验值在压力特性方面:FSI和CFD的出口压力平均值更符合实际,试验出口压力均值略低。结合对比分析和FSI理论得出FSI的仿真更接近真实;
(2) 通过对比内外转子间流体域某一截面速度和压力得出:在吸油区域计算得到的负压CFD大于FSI,计算得到的速度CFD小于FSI;在排油区计算得到的正压力CFD大于FSI,计算得到的速度CFD小于FSI的结果;
(3) 通过对比内外转子与流体耦合界面某点处的压力分布得出:CFD的压力随时间的波动值均大于FSI的压力值。
综合以上分析得出:CFD和FSI的计算结果均存在差异,由于CFD在运动界面上只指定了运动,而FSI在流固耦合界面处流体不仅产生运动,而且受到固体的作用力,通过对比发现耦合对计算结果有很大的影响,对泵进行FSI耦合分析使得分析结果更加真实,更有利于对泵的流场和转子动力学特性进行分析。
