谐波齿轮传动中柔性轴承的力学分析

刘 欢 邢静忠

(天津工业大学机械工程学院，天津300387)

谐波减速器因体积小、质量轻、回差小、定位精度高、传动效率高，在工业机器人、高档轿车、航空航天、光学仪器、通用机械等领域广泛应用。而柔性轴承作为谐波减速器的关键零部件，对谐波减速器的运转平稳性、重复定位精度、回转精度以及工作的可靠性等关键性能指标具有重要影响。

谐波减速器主要由柔轮、柔性轴承、波发生器和刚轮组成，如图1所示，其传动原理为：当椭圆波发生器装入轴承后，由于轴承内圈和波发生器为过盈配合。波发生器使轴承内壁强制变形成椭圆，使轴承内壁和波发生器表面贴合。轴承内圈将变形传递给滚珠，波发生器强制内圈变形后，将滚珠顶到指定位置，滚珠分布曲线为内圈椭圆廓线的等距线，滚珠再将变形传递给外圈，强制变形使外滚道产生径向位移和轴向位移。外圈将变形传递到柔轮上，实现齿圈啮合。外圈因承受较大的波动变形而易发生破坏失效。

图1 谐波减速器示意图Figure 1 Harmonic reducer

1 采用的方法

国内外学者均未考虑杯型柔轮锥度变形后，轴承外圈的锥度变形和滚珠滚道的受力状态。我们采用有限元分析的方法，先建立装配状态下柔性轴承滚道和滚珠模型，研究滚珠达到预定位置后，外滚道的径向位移及周向位移以及滚道和滚珠的接触应力。然后考虑柔性轴承装入锥度变形柔轮后的接触状态和柔轮变形状况，及轴承外圈的受力状况。对柔性轴承装配状态下的变形和应力进行分析，有助于对柔性轴承的设计提供指导。

2 模型概述

柔轮和柔性轴承是其关键部件。因此以柔性轴承和柔轮的参数为主要参数。通常有25-120，32-80，32-120等型号。以32-80型减速器为例进行研究，其速比为80，齿形模数0.5 mm，齿圈宽度11 mm，齿圈厚度为2 mm。

在有限元中建立滚珠和外滚道实体模型。其结构参数见表1。材料弹性模量内外滚道为2.07GPa，滚珠处为2.17 GPa，泊松比均为0.3。滚道采用SOLID86单元，滚珠采用SOLID45单元。

表1 结构参数Table 1 Structure parameters

柔性轴承和普通轴承不同之处在于内外圈轴承壁很薄，易于变形，在装入波发生器的情况下产生强制变形。椭圆波发生器是最常见，应用最广泛的一种波发生器，以椭圆波发生器为例。

由于轴承外圈和内圈之间有多个不断滚动的滚珠。首先要解决的问题是内圈变形后，哪些滚珠对外滚道有力的作用，接触力为多少？

当变形后的轴承装入柔轮时，柔轮产生锥度变形，分析锥度变形时，必须要解决柔轮对轴承外圈的相互作用。采用有限元分析的方法来分析外滚道和滚珠之间的受力和变形能有效避免Hertz理论中摩擦、预应力和预变形的影响。采用ANSYS对装配状态下的柔性轴承进行分析，而接触本身为高度非线性行为，接触区域的网格粗细和接触刚度的设置对结果影响很大。六面体网格在相同网格尺寸的情况下可以得到更为精确的解，因此采用六面体网格。为进一步提高结果的准确性，还需要合理的网格划分和边界条件。

3 椭圆凸轮作用下的轴承变形

3.1 轴承模型的实体网格划分

应用有限元求解接触问题时，网格尺寸和接触参数直接影响分析结果的精度。对滚珠及内外圈进行网格划分，选择ANSYS的SOLID186单元；运用扫掠和映射的方法对模型进行六面体网格划分；整体网格尺寸为0.4 mm，接触区域进行网格加密尺寸为0.1 mm。取180°范围内滚轴与外圈的模型建立接触，外滚道模型接触区域如图2所示。

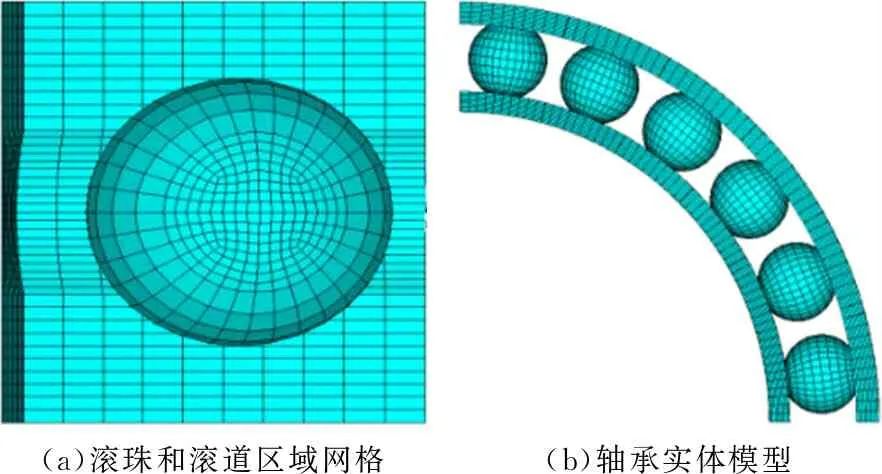
(a)滚珠和滚道区域网格(b)轴承实体模型

3.2 滚珠的径向位移

取外滚道圆心s3=32.228 mm，滚道半径r3=4.088 mm，滚珠半径rz=3.75 mm。假设滚珠在装配状态与外滚道贴合，半径为r=s3+r3-rz，最大径向位移w0=0.5 mm。a=33.066 mm为滚珠分布的长轴位置，b=32.079 mm为滚珠分布的短轴位置。

依据滚珠分布的任意角度φ位置椭圆极径ρ建立方程，可以求得不同φ角处的滚珠径向位移。柔性轴承内圈与椭圆凸轮是过盈配合。内圈变形成椭圆，内圈将变形传递给滚珠。滚珠受到保持架的约束呈等距分布。故滚珠分布为椭圆廓线的等距线，取6个等角度分布的滚珠。从距离长轴φ=7.5°处开始，两个滚珠间相隔15°，分别代入滚珠的φ角，根据椭圆等距线方程可求得径向位移。

3.3 滚珠作用下的外滚道位移

取轴承外圈为研究对象，求解得到变形结果如图3所示。从图3可以看出：滚珠椭圆等距线分布的理论是正确的。约束滚珠的周向位移，提取外圈径向位移可以看到长轴处存在最大径向位移为0.4896 mm。与理论计算中输入的最大径向位移0.4821 mm基本一致。

图3 滚珠作用下的径向位移Figure 3 Radial displacement operated by balls

由于滚珠不断周向滚动分布，因此采用滚珠关于长轴对称分布。滚珠正好在长轴两侧对称位置，故在滚珠上施加位移后，提取长轴的径向位移与理论值存在较小的计算误差。将计算所得位移分别施加在滚珠上，得到变形结果见图3。提取各个滚珠处的径向位移与理论结果吻合性较好。

4 柔轮装配状态下的轴承锥度变形

4.1 实体模型的建立

柔轮结构参数：筒体长度50 mm，柔轮内圈半径37.325 mm，杯底孔半径10 mm，齿圈厚度2 mm，壳体厚度1 mm，齿圈过渡圆弧50 mm，齿圈宽度11 mm，杯底倒圆半径2 mm，最大径向位移0.407 mm。根据上述参数建立柔轮实体模型。

先建立柔轮的外圈轮廓，在杯底和筒体连接处做圆弧处理，在齿圈和筒体连接处做圆弧处理，沿轴向旋转90°得到柔轮模型；建立半径和柔轮内壁相等的轴承外滚道模型进行装配。

4.2 多级接触的建立

一级接触为外滚道和柔轮之间的接触，二级接触为滚珠和外滚道之间的接触。根据上述参数建立柔轮实体模型，对柔轮外滚道和滚珠分别采用CONTA185，CONTA173，CONTA170。对柔轮杯底施加全约束，对轴承外滚道径向施加对称约束。依次对从长轴处到短轴处的滚珠将算得的径向位移0.4821 mm，0.3471 mm，0.1171 mm，-0.1426 mm，-0.3626 mm，-0.4875 mm施加在各滚珠上，这些径向位移施加于垂直法线方向。

4.3 锥度变形分析

在轴承滚道外表面建立前、中、后三条路径，得到轴承外圈前、中、后三个截面的径向位移见图4。从图4可以看出在长轴处前截面径向位移最大，后截面径向位移最小。在短轴处前截面偏差为6%，后截面为14%。在长轴处均为12%左右。主要是由于轴承外圈装入柔轮后存在径向变形，长轴处柔轮内壁挤压轴承外圈后截面，前截面翘起。而在短轴处柔轮挤压轴承前端面，使其缩小量最大，后端面径向位移绝对值最小。

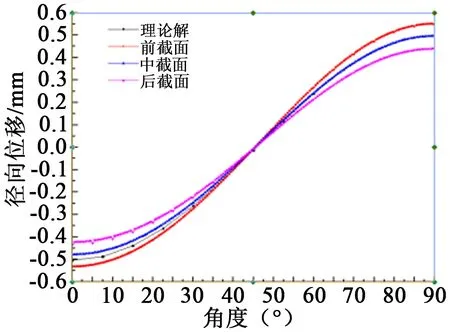
图4 外滚道变形后的径向位移Figure 4 Radial displacement of outer raceway deformation

图5为滚道和柔轮接触区域图。从图5可以看出，滚道和柔轮的接触区域在长轴处主要为后端面接触，在短轴处主要为前端面接触，从长轴到短轴，接触区域逐渐从后端面向前端面移动。

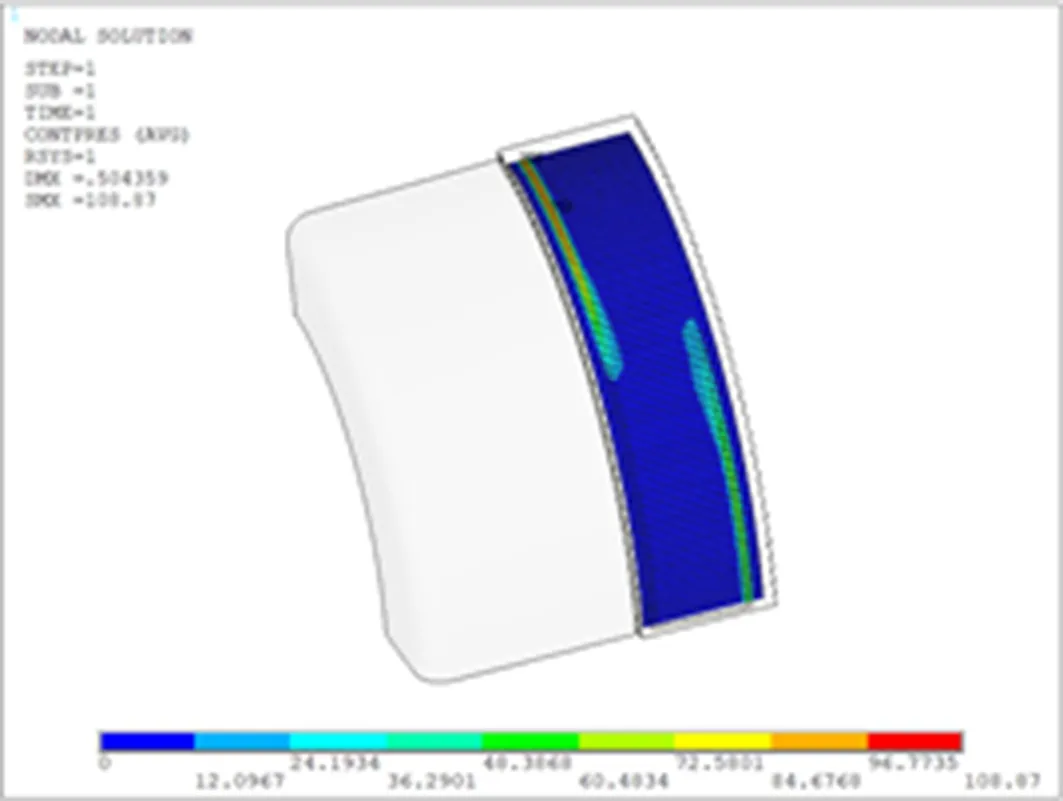
图5 接触区域图Figure 5 Contact zone

从图6可以看出，对滚道有力的作用的滚珠有三个。第1个滚珠与长轴之间的偏转角度为7.5°，第2颗滚珠与长轴之间的偏转角度为22.5°。可以看到：越靠近长轴处滚珠受到的接触力越大，最大接触压力648.737 MPa发生在最靠近长轴的滚珠与滚道接触位置。

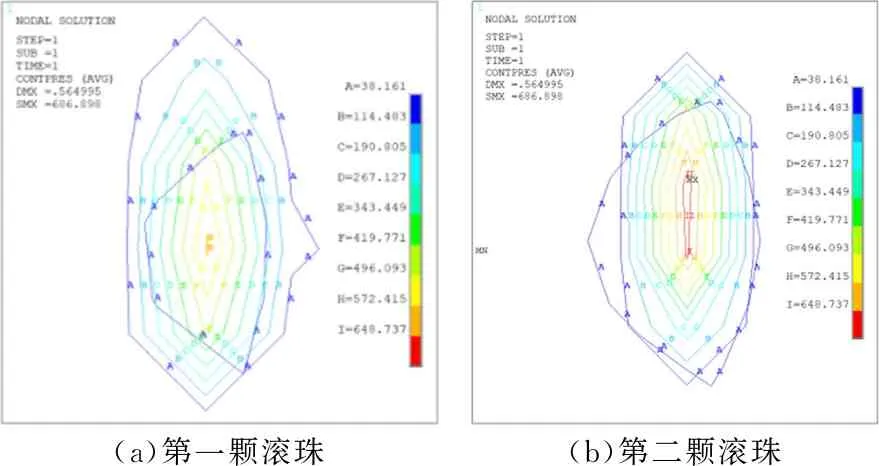
(a)第一颗滚珠(b)第二颗滚珠

5 结论

(1)椭圆波发生器装配状态下，轴承外圈只受到三个滚珠的作用力，且越靠近长轴位置处其接触力越大。对关于长轴对称的滚珠施加径向位移约束，其长轴处径向位移与理论值基本一致。

(2)当变形后的柔性轴承装入柔轮时，轴承外圈存在锥度变形。长轴处柔轮内壁挤压轴承外圈后截面，前截面翘起，而在短轴处柔轮挤压轴承前端面使其缩小量最大，后端面径向位移绝对值最小。故柔轮在长轴处对柔性轴承靠近杯底的内侧挤压，短轴处则在外侧挤压。

(3)当椭圆波发生器装配状态下的轴承装入柔轮时，滚珠和滚道之间的接触力从长轴到短轴处依次递减，最大接触力发生在靠近长轴位置处的滚珠。