一种非局部连接的抗噪性储备池构建方法

吴一凡，陈云华，张 灵，陈平华

(广东工业大学计算机学院，广东广州 510006)

1 引言

液体状态机对比人工神经网络，具有抗噪性强、鲁棒性强等优势，并在时序任务处理和多任务处理上具有一定的优势.但其在具有上述优势的同时，优化也更难进行[1].文献[2]采用了脉冲时序可塑性算法(spike-timing-dependent plasticity，STDP)算法对储备池进行优化，由于采用欧氏距离作为度量标准，而欧式距离无法对脉冲序列的相似性进行有效刻画，因此，该方法无法保证优化的有效性.同时，采用脉冲时序依赖可塑性算法的进行无监督优化也会导致储备池对样本产生依赖性，与储备池本身高泛用性的理念不符.而文献[3]则模仿深度神经网络，串联了多个储备池，储备池间采用误差梯度下降的方式进行训练.由于脉冲神经网络所传播的是脉冲信号，与人工神经网络的模拟信号有着本质区别，导致在采用此类方法时需要对网络信号进行两次的信号转换，而在信号转换时脉冲信号只会被保留频率信息，因此这种优化方式同样不能保证优化的有效性.还有部分文献依据生物神经系统内抽象提取出的规律进行储备池[4]，此种储备池的优化方式所具有的生物真实性可媲美真实生物系统，可以反过来支持真实的生物神经系统训练，但是这也导致优化算法非常复杂.研究表明，在大脑中普遍存在功能柱的现象，不同的大脑区域分别负责不同的任务，而在各个功能柱间的非局部连接服从伽马分布[5].为了提高储备池的泛用性和抗噪性，同时避免复杂的优化过程，本文模拟大脑中的这种非局部连接方式，采用伽马分布来生成储备池的权值，生成一个具有更高生物真实性、隐含功能柱结构的储备池.首先，通过对储备池活动和储备池进行Lempel-Ziv复杂度分析，从理论上证明该种储备池权值生成方式的优势;然后，通过与STDP和高斯分布等进行对比实验，证明本文采用伽马分布生成的储备池具有更高的准确度和更强的抗噪性.

2 基于伽马分布的储备池权值生成及网络Lempel-Ziv复杂度分析

通过对储备池神经元活动的直观观察，可以看出人工神经网络优化方式并不适用于储备池的优化.本节将对比伽马分布与其它分布及优化方式的Lempel-Ziv复杂度，以此来从理论角度说明伽马分布生成储备池权值的优越性.

2.1 基于伽马分布的储备池权值生成

现有的液体状态机(liquid state machine，LSM)多采用均匀分布或正态分布来生成储备池内部连接的权值.然而，均匀分布或正态分布只是大脑中某些局部的内部连接方式，实际上，在非局部的连接中，伽马分布起着更重要的作用[5];并且，均匀分布和正态分布的通用性太强，使得针对特定应用的网络，在准确率和生物真实性方面都有待提升.结合大脑中普遍存在的自组织现象所形成的功能柱[6]现象，本文采用大脑中各个局部间连接所采用的伽马分布来生成储备池的内部连接，在提高生物真实性的前提下，同时注重泛用性和针对性.

本文采用LIF神经元和静态突触来构建储备池.在这里静息电位Vresting取0，阈值Vthresh取0.025 mV保持阈值与静息电位间的差值.不在神经元模型中引入外部噪声，即Inoise=0.外部持续电流Iinject也设置为0.共采用200个神经元构建储备池.不考虑神经元间的相对位置，两个神经元间的连接概率为10%.根据文献[1]，结合本文所用的储备池神经元数，网络的权值大小应在()之内.考虑到直接截断标准伽马分布所得权值会导致权值的分布与伽马分布产生较大的偏差，本文采用调整标准差的方式来保证权值落在上述范围之内，即将伽马函数的均值和标准差分别设置为0和0.98.伽马分布的密度函数及均值和方差如下:

采用MATLAB内置的伽马分布函数来生成权值所需数据.输入与储备池之间以10%的概率连接，连接权值采用[-1，1]的均匀分布.

2.2 网络Lempel-Ziv复杂度分析

Lempel-Ziv复杂度，能帮助笔者更准确的分析权值生成和优化方式对于网络的活动的影响，能一定程度上定量分析出网络活动的复杂度，并据此分析网络对输入的敏感程度和记忆能力.Lempel-Ziv复杂度是由Lempel和Ziv提出来的[7]一种对离散信号序列复杂度进行计算的方法，该方法将离散的信号转化为有限的符号序列，通常情况下是二值的符号序列，然后计算该序列中新模式出现的速率来表征该序列的复杂度.

记二进制序列为S，长度为n，将S 划分为S(1，h1)S(h1+1，h2)S(h2+1，h3)…S(hn-1，hn).当∀S(hn-1，hn)S(hn，hn+1)时，称为穷尽S的一个划分，记为E(S).记cE=|E(S)|表示满足E(S)划分的子序列的数量.此时，将

称作Lempel-Ziv复杂度.Lempel-Ziv复杂度越高，表示序列的多样性和复杂性越高，越低表示序列的重复性周期性越强.本文将计算储备池网络中神经元的整体放电状态的复杂度.

为使对比更具说服力，本文储备池网络的参数设置，采用与文献[8]相同的值.参数设置完毕，向网络输入随机值，并记录网络的活动.由于本文所用的脉冲神经网络可以直接记录脉冲时间作为状态，因此，在计算Lempel-Ziv复杂度时，可省去将连续变量转变成二值变量的步骤.将包含脉冲的时间间隔记录为1，将不包含脉冲的时间间隔记录为0即可直接计算复杂度.

通过图1(a)可以看出，使用伽马分布生成的储备池网络的Lempel-Ziv复杂度远远低于另外两种方式.并且，神经元膜时间常数的变化几乎不会对网络的Lempel-Ziv复杂度产生影响.Lempel-Ziv复杂度低，说明基于伽马分布生成的储备池网络对输入的记忆能力非常强，对于输入的敏感程度和受噪声及小部分数据损坏的影响非常小，即具有更强的抗噪性.同时，由于储备池所产生的模式具有很强的周期性，能够使用更为简单的读出函数来执行任务，即对读出函数的要求更低，线性读出函数所能执行的任务更丰富.

鉴于文献[8]并没有明确是哪种时间常数，同时为了进一步探讨该种网络结构对膜时间常数的敏感程度，增加针对突触膜时间常数的实验，实验结果如图1(b)所示.可以看到，在突触膜时间常数小于0.04 s时，膜时间常数对Lempel-Ziv复杂度几乎没有影响，其后随着膜时间常数的上升，Lempel-Ziv复杂度上升，在超过0.1 s后受限于模板本身的复杂度而趋于平缓.分析图1不难得出，采用伽马分布的前提下，神经元膜时间常数对于Lempel-Ziv复杂度的影响很小，解决了脉冲神经网络普遍存在的参数难以调整的问题.而突触膜时间常数的取值范围要小于神经元膜时间常数，在本文神经元时间常数取0.01 s的前提下，遵循该取值范围的突触膜时间常数对Lempel-Ziv复杂度几乎没有影响.可以得出结论，采用伽马分布生成储备池，在提高网络计算性能的前提下，还能大大的降低网络的调参难度.

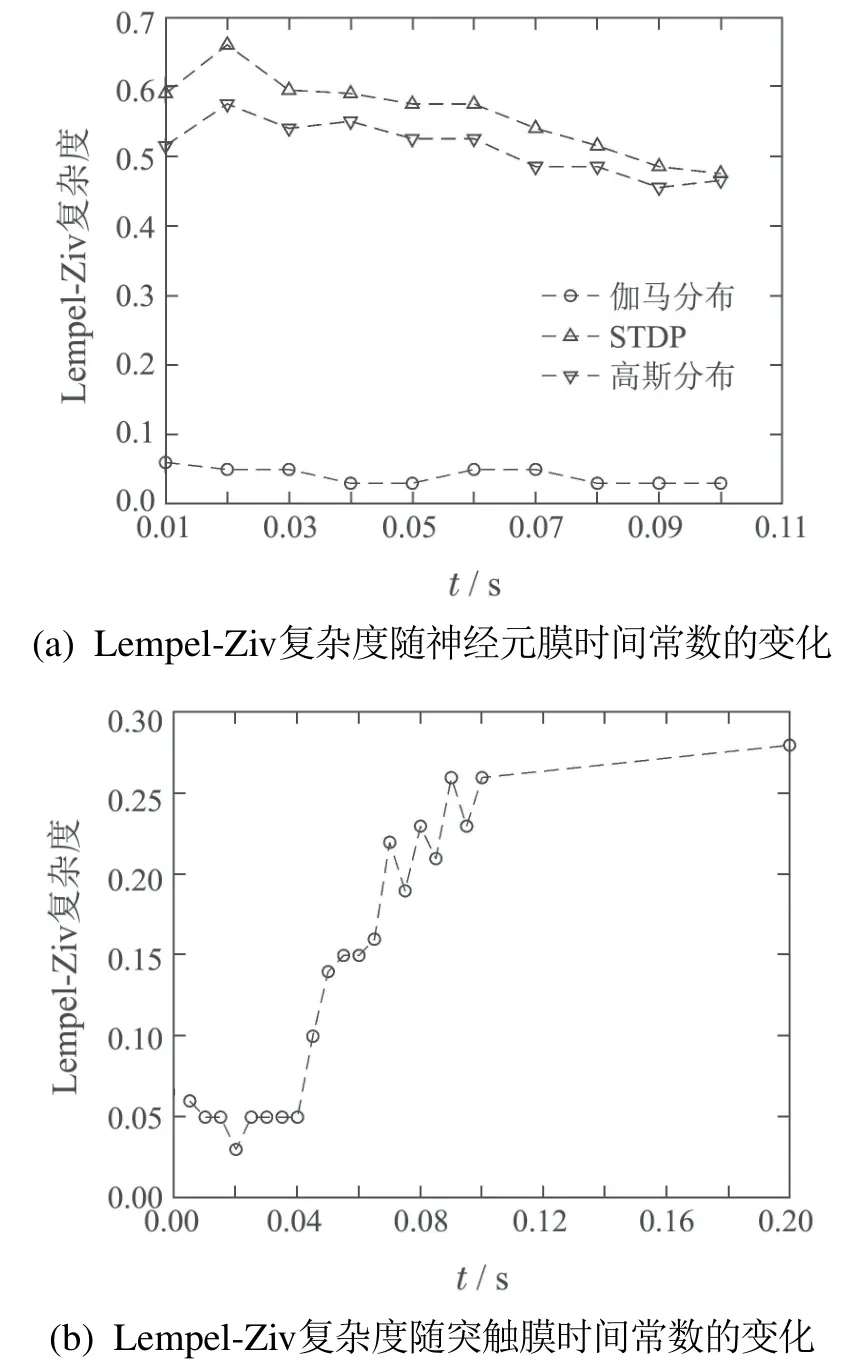
图1 Lempel-Ziv复杂度随不同膜时间常数的变化Fig.1 The Lempel-Ziv complexity with different time constants

3 网络构建与实验结果分析

实验使用软件CSIM[9]在MATLAB 2018a上实现.使用MNIST库进行实验.实验随机选择5000个训练样本进行训练，并用全部10000个测试样本进行测试.

3.1 储备池构建

3.1.1神经元模型

脉冲神经元模型有许多，例如Hodgkin-Huxley(HH)模型(式(4))、integrate-fire(IF)模型、Leaky-integrate and fire(LIF)模型(式(3))、resonate-and-fire(RF)模型、Izhikevich(IZH)模型等.其中HH模型是最精确的，其精确程度不仅仅局限于神经元反应，更体现在其反应机制，从微观的层面模拟了生物神经元.HH模型在进行模拟时效果很好，但是其缺点也很明显，计算量大，速度慢.而IF神经元和LIF神经元是HH的一种简化形式，保留了其大部分的反应模式，去掉了微观层面各种参数，去掉了神经元反应的细节，仅保留了其发放脉冲的反应，大大的降低了计算量.LIF模型动力学方程为

其中:Vm为膜电位，Vresting为静息电位，Rm为电阻，Isyn为后突触动作电位，Iinject为外部持续电流，Inoise为外部噪声，τ为膜时间常数.输入信号会累加在膜电位上，当膜电位Vm大于阈值Vthresh时，神经元形成一个动作电位即向外发放一个脉冲，然后膜电位重置为静息电位.

HH模型动力学方程为

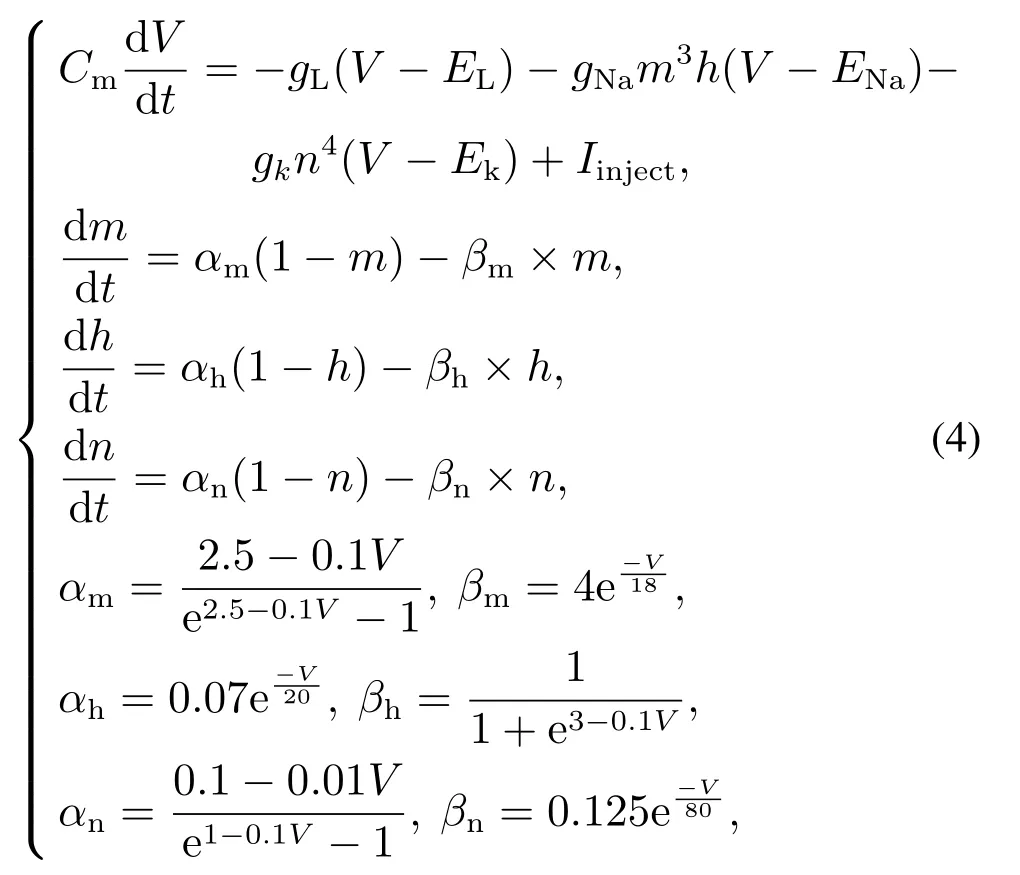
式中:C为膜电容，g为离子通道电导，E为对应离子的逆转电位，都是常数;V 为膜电位;m，h，n为不同通道的激活参数和失活参数;Iinject为外部输入电流.可以看到HH模型的参数非常多，动力学方程非常的复杂.本文储备池使用LIF神经元模型，因其较容易实现且在保证脉冲发放仿真度的前提下参数较容易设置.同时，LIF神经元的膜电位积累的过程能被充分的展现出来，而HH模型因其真实性太高，模拟过程中保留的是真实的动作电位，使得神经元膜电位的活动看起来并不明显.HH模型着重展示动作电位的真实情况，较容易观察到发放的活动，但也导致膜电位的变化不够明显.而LIF神经元则将动作电位简化为膜电位的重置，着重展示发放前膜电位的积累情况，这使得在提取网络状态时，有充足的膜电位活动用以提取并进行进一步处理.

本文用在后续实验中的LIF 神经元的静息电位Vresting取0，阈值Vthresh取0.025 mV 保持阈值与静息电位间的差值.为了简化计算，不在神经元模型中引入外部噪声，即Inoise=0.而外部持续电流Iinject，由于网络并不需要其作为逃脱噪声以维持活跃，故也设置为0.于是，神经元模型为

3.1.2 储备池神经元个数及连接

本文选择用200个神经元来建立储备池.为了保留更多的输入信息，同时使输入信号对储备池产生更大的影响，构建储备池时使其中抑制性神经元占20%而兴奋性神经元占80%[10].神经元间的连接采用随机的方式生成.因神经元数较少，不考虑神经元间的拓扑结构.整个储备池内的神经元以10%的概率连接，允许连接自身.各个神经元间的连接采用同种突触.

3.1.3 数据编码方式

本文采用的编码方式为把一张图片编码成一串脉冲，以脉冲发放时间点来传递信息.在进行模拟前，需要先把手写数字图像转化成脉冲信号.本文将每张图片转化为一个脉冲序列，以脉冲发放时间作为信号载体.先将灰度图转化为二值图，然后将二值图像按行排列成一个长行向量，按每1 ms编码一个脉冲的间隔，在有非零像素值的相应位置编码一个脉冲.例如，第5个像素点处有非零像素值，则在5 ms处编码一个脉冲.整个图像最终被编码成一个最大脉冲数为784的脉冲序列.脉冲序列会输入到一个神经元中，模拟时间为1 s，让储备池能够有充分的时间在信号消失后产生“回声”用于展示各个模式间的共同点和不同点[11].

3.2 突触模型

式(6)为静态突触的模，其中:Vm为膜电位，A为缩放系数，tf为发放时间，τ为膜时间常数.式(7)为动态突触的模型，其中:U，D，F为动态突触参数，Ak为后突触动作电位，Δk表示第k个脉冲与第k+1个脉冲的间隔.初始状态为u=U，R=1.本文实验需要较快的储备池变化速度，使用动态突触模型可能造成过拟合的问题，故使用静态突触模型进行实验.

本文的突触膜时间常数设置为神经元膜时间常数的一半.后突触动作电位选用指数函数形式(见式(6)).权值直接采用随机的方式生成.在区间上生成一个均值0标准差0.98的伽马分布.负的权值代表相反的神经信号.权值的另一个作用是调整整个网络的活动情况.权值整体绝对值越大网络越活跃，变化速度越快，记忆时间越短.网络活动程度的变化与权值的绝对值大小成指数相关.当权值绝对值太大时，网络活动呈现混沌，需要对输入进行处理以控制混沌的轨迹.在这里避免混沌的出现，将权值的按比例缩小至权值谱半径为1.网络的输入同样由突触传递入网络中.连接输入神经元的突触与储备池突触大部分参数一致，但采用不同的权值生成方式.输入权值为(-1，1)区间上生成的一个标准正态分布.

3.3 读出函数

在储备池计算中，读出函数的形式多种多样，只要能够将储备池中的状态提取并转化成所需要的结果，都可以算作是读出函数.

本文读出函数采用两层的BP网络.隐藏层神经元200，激活函数为sigmoid，输出层10个神经元，激活函数为softmax.网络的训练采用量化共轭梯度法(scaled conjugate gradient，SCG)，代价函数为交叉熵代价函数.因为读出函数是一个传统的BP神经网络，其信号要求为模拟信号，故储备池的输出也要是模拟信号，即频率.这里采用标准非线性反应函数r=tanh(Vm)来定义频率，以此来提取储备池的状态并作为读出函数的输入.

3.4 实验结果与分析

3.4.1 时间序列分类任务

分类任务采用泊松脉冲模板进行.模板的长度为1 s，随机生成150 Hz的泊松脉冲序列，并根据分类数决定模板数量.对每个模板的每个脉冲生成一个偏移量.偏移量在[-4，4]中采用正态分布生成.生成的各类模板总数为100个训练样本、100个测试样本，100个样本中每类模板所占数量随机.这样设置主要是为了在评测时序任务分类的同时评测网络的抗噪性和鲁棒性.

实验采用线性的读出函数WoutX=Ytarget来进行分类任务.统计10次独立实验的准确率来作为最终的准确率.图2为不同储备池内部权值生成方式下的准确率曲线.图例中的均匀分布和伽马分布为权值生成方式，STDP为生成后储备池的优化方式.

图2 对随机输入脉冲串的识别准确率Fig.2 Accuracy of random spike trains

可以看出，采用伽马分布生成的储备池在进行二分类时，准确率高达99.5%，远超均匀分布和均匀分布生成后使用突触可塑性(synaptic time dependent plasticity，STDP)进行优化的储备池.在类别数小于10时准确率都比采用均匀分布和STDP优化的储备池高.而采用的样本都是总数为100，样本内部各类别具体数量随机的样本.足以说明采用伽马分布生成的储备池的泛用性更高，鲁棒性更强，对样本的依赖性更小.STDP作依赖性更小.脉冲时序依赖可塑性算法作为一个具有高生物真实性的算法，利用其对储备池进行优化后获得的储备池的性能，不如采用具有高度生物真实性的分布生成权值所构建的储备池，可见采用具有高生物真实性的分布进行权值生成，对于提升储备池性能非常重要.同时也说明了，不能对储备池进行随意优化，更不能通过不具生物真实性的方式对储备池进行优化.

3.4.2 无噪声数据分类

本节进行的实验使用的是数据库的原始数据，没有加入噪声信号.采用MNIST，POSTURE和UCF-101三个数据库进行实验，实验均采用小样本训练的方式进行.对于MNIST，实验从训练集中随机选取5000个训练样本进行训练，不分类别，并用全部10000个测试样本进行测试.POSTURE数据库随机选取20%的样本进行训练，同样不限制每一类样本的数量，并用剩下的所有样本作为测试集.对于UCF-101数据库，随机选择其中的两类，并在这两类中各随机选择一个视频进行单样本的训练，将每类剩下的所有样本作为测试集.本文侧重于展现储备池的作用，因此在实验时需要排除读出函数的影响.本文的的读出函数全部采用最简单的两层BP神经网络，并采用最原始的BP算法进行训练，储备池输出的状态信号直接作为网络的输入，输出层采用竞争算法，10个神经元分别代表十类.神经网络的训练通常能较快的收敛.无噪声实验的实验结果如表1所示.其中的各种分布为生成储备池权值所采用的分布，STDP则表示生成储备池后采用STDP算法进行优化.

表1 无噪声数据实验结果Table 1 Accuracy without noise

可以看到，本文所构建的液体状态机效果是最好的.采用人工神经网络思想进行优化，只能提高生物真实性相对较低的高斯分布生成的储备池，而且提升后的性能依然不如本文所采用的伽马分布生成的储备池.对于伽马分布生成的储备池，优化后甚至会有反效果.从表中可以看到，对于具有高度生物真实性的储备池，基于人工神经网络的优化思想，使用STDP来进行优化是不能保证有效性的.这也证明了储备池的构建和优化方法需要保证其具有较高的生物真实性.

3.4.3 带噪声的数据分类

为了验证网络的抗噪性能，进一步进行噪声数据实验.实验所用噪声数据在MNIST基础上生成.使用高斯分布来生成噪声信号，并将噪声信号加到原数据上作为测试样本进行测试.对噪声信号的分类，采用伽马分布生成权值的储备池进行.同样采用在训练集中随机选取的5000个原始训练样本进行训练，并采用全部的测试样本添加噪声信号后进行测试.其中噪声采用均值为0，方差为0.1，0.2的高斯分布来生成.实验结果如表2所示.其中高斯分布和伽马分布为生成储备池所用的分布，STDP为生成后优化的方式.

表2 噪声数据实验结果Table 2 Accuracy with noise

从表2可以看到，方差0.2以内的噪声对伽马分布生成储备池的正确率的影响在0.2%以内，说明采用伽马分布生成的储备池有较强的抗噪性.而经过STDP优化的储备池，在加入方差为0.1的噪声后，准确率就出现了0.4%的下降，更是在方差为0.2的噪声信号加入后，骤降5%，抗噪性甚至不如某些使用具有生物真实性激活函数的人工神经网络.进一步说明了，储备池的构建和优化要以生物真实性为主要依据.

3.5 结果分析

目前大脑依然是世界上最复杂最精细的系统，本文算法的效果得益于其生物真实性.

本文算法训练所使用的只有随机选取的5000个样本.在采用伽马分布生成储备池权值的情况下，依然能达到93.45%的准确率.而即使是卷积神经网络，在这种条件下也只有91%左右的准确率.从LIF神经元的活动方式可以看出，单一孤立的输入和非常密集的输入都会被自动的过滤掉.且在储备池中，尤其是在输入消失的时间段内，充满了稀疏的微回路的储备池形成的是层层嵌套的筛选.这种能力最终会筛选出某种特定的模式，甚至在不需要训练的情况下能够直接将不同的模式分开[12].在储备池中，输入压制混沌现象主要是通过改变混沌的轨迹实现的，而不是直接改变其表现形式[13-14].这更进一步证明了储备池具有较强的抗噪性与鲁棒性.而这些特性，皆由其生物真实性所带来，随着生物科学与混沌理论的进步，可解释性会越来越强，也会越来越可控.

4 总结与展望

为了增强对网络的放电噪声的抑制和对输入信息的提取能力，本文保留了20%抑制性神经元.并在此基础上采用伽马分布来生成储备池内部连接权值，以此来获取一个具有强生物真实性，同时隐含功能柱概念的储备池.通过理论分析及与其它常用分布和分簇自组织的方法进行对比，得出使用伽马分布所构建的储备池在进行模式识别时具有更高的精度和更好的抗噪性能的结论.

本文使用时间序列分类任务来评价液体状态机模型的性能.时间序列信息的处理能力是脉冲神经元网络最基本的能力，虽然它能够代表网络的性能，但是探究网络对更复杂的任务的执行情况更有价值.储备池最大的优势是时序任务的实时处理能力及小样本学习的能力，因此本文未来将使用实时采集的时序信号进行进一步研究.