结合前馈调参与迭代学习的数据驱动控制方法

薄雨蒙，曹明生，高慧斌

(1.中国科学院长春光学精密机械与物理研究所，吉林长春 130000;2.中国科学院大学，北京 100049)

1 引言

在运动控制系统中，前馈控制得到了广泛的应用，特别是在对控制精度要求很高的轨迹跟踪任务中，前馈控制可以取得良好的控制效果.前馈控制器基于先验知识获得前馈控制信号对误差进行补偿，因此可以有效提高控制精度.传统的前馈控制方法包括迭代学习控制(iterative learning control，ILC)，基于模型的前馈控制和迭代前馈调参(iterative feedforward tuning，IFT)等.

迭代学习控制适合于具有重复性的控制任务，它由Arimoto等人[1]于1984年提出，之后几十年发展出了多种扩展的方法[2-3]，并可以与其他控制方法，如自适应控制[4-6]、鲁棒控制[7-9]和模糊控制[10-11]等进行结合，根据系统特性和控制需求，可以达到更好的控制效果.

迭代学习控制利用以前迭代周期获得的信息，通过学习方法估计并补偿系统中存在的不随迭代次数变化的扰动.但在控制过程中，非重复性扰动存在积累现象，从而影响控制误差的收敛性[12].传统的学习律学习的是系统的控制输入，这要求期望轨迹在迭代域上严格重复，一旦轨迹发生变化，迭代学习控制将会失效[13].针对期望轨迹变化的情况，文献[14]提出了分段ILC，在文献[15]中以分段ILC为基础，将任务分解为多个子任务进行单独学习，但其控制性能受分段方式影响，并且增加了算法实现的复杂度.

相反，基于模型的前馈控制也可以达到较高的控制精度，但期望轨迹的变化不会引起控制效果的恶化[16-17].基于模型的前馈控制使用系统逆模型或系统敏感度函数建立学习滤波器，利用系统信息进行前馈补偿，获得的控制效果依赖于系统模型的质量[18].但在工程应用中，对复杂系统建立精确模型难度大，成本高，更倾向于使用数据驱动控制方法，即直接使用输入输出数据进行控制器设计的方法[19-20].

采用基函数可以将迭代学习控制与基于模型的前馈控制的优点相结合，获得适用于变轨迹任务，高控制精度且不依赖于系统模型的前馈控制方法[21].通过基函数的引入，信号被投影到基函数张成的空间中，组成的前馈控制器可用于估计系统的逆模型[22].

使用基函数将前馈控制器参数化，可以将系统模型辨识问题转换为参数化前馈控制器的迭代前馈调参问题，并通过最优化方法得到最优前馈控制器[23-24].文献[25]使用数据驱动的梯度下降法进行调参，但文献[25-26]证明此方法在存在噪声时将得到参数的有偏估计，因此引入辅助变量来获得参数的无偏估计，文献[27]对参数估计的精确度进行了分析.文献[28]提出了高阶的优化方法，使用过去所有迭代周期获得的误差信号进行参数估计，算法具有高精度和高噪声容忍度.文献[29-30]使用有理基函数以获得更高的精度.

将ILC与IFT进行比较，发现ILC对于重复性任务可以得到很高的控制精度，但期望轨迹的变化会引起极大的效果恶化[30];反之，IFT则适用于变期望轨迹任务，不依赖于系统模型，但控制精度低于ILC.

为了在保证高控制精度的同时，改善ILC在期望轨迹变化时的效果恶化问题，本文针对执行变轨迹步进扫描运动的系统，提出了一种将IFT与ILC进行结合的数据驱动的控制结构.通过引入IFT，得到最优系统前馈控制器，消除期望轨迹引入的扰动，提高轨迹变化时的控制精度;通过ILC，消除系统重复性扰动，进一步提高控制精度.在IFT的计算过程中，引入输入整形滤波器，在保证梯度下降法计算精度的同时简化了计算过程.本文提出的算法在轨迹变化时仍能保证高控制精度，同时是一种数据驱动控制方法，可以直接应用于不同工业系统而不依赖于系统的先验信息.

2 问题提出

2.1 控制结构

控制系统框图如图1所示，其中:C是反馈控制器，Kff是参数化前馈控制器，Ky是输入整形滤波器，KILC是迭代学习控制器，KIFT是系统前馈控制器.实际系统的系统模型P可以看作离散单输入单输出线性时不变系统.系统传递函数可以写作

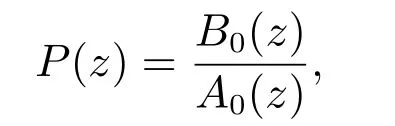
其中B0(z)，A0(z)∈R(F).此外，已知参考信号r是对预先规划好的n阶连续可导的轨迹以采样时间Ts采样得到的N个点的序列，ry是经过输入整形滤波器得到的整形参考信号，y是系统输出，ey是整形参考信号ry与输出y之间的误差，uff为Kff输出的前馈控制信号，ufb为反馈控制器C输出的控制信号，uILC为迭代学习控制器离线输出的前馈控制信号，uIFT为KIFT输出的系统前馈控制信号.所有信号都为以采样时间Ts进行采样的n维离散序列.

图1 控制结构示意图Fig.1 Control configuration

本文提出的控制方法在参数估计阶段和迭代学习控制阶段使用不同的控制结构.在系统控制框图中，对虚线框表示的迭代调参前馈控制器Kff和输入整形滤波器Ky通过基函数进行参数化，并通过最优化迭代调参算法迭代估计收敛的最优参数值.当迭代调参过程结束后，移除控制框图中的虚线部分，并将最优参数值输入到系统前馈控制器KIFT中，此时的控制结构是由前馈控制器和迭代学习控制器组合成的迭代学习控制结构.

2.2 参数化的前馈控制器和输入整形滤波器

如图2所示，前馈控制信号uff可以由期望轨迹r和参数化前馈控制器Kff(θff)表示为

同时，整形参考信号ry可以由r和参数化输入整形滤波器Ky(θy)表示为

其中Kff(θff)和Ky(θy)由定义1给出.

图2 加入输入整形滤波器的迭代前馈调参框图Fig.2 Configuration of IFT with input shaping filter

定义1通过引入基函数，参数化前馈控制器Kff(θff)和输入整形滤波器Ky(θy)可表示为

其中:

多项式基函数表示为

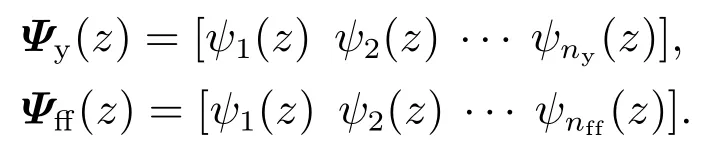
各项基函数为

其中nff和ny为构成Kff和Ky的基函数的个数.通过基函数，可以将输入信号分解为各阶导数.因为所有的ψi(z)都是关于z的函数，为了简化表示，在后文中省略z.此外，为了简化，还将Ψy和Ψff组合为一个向量Ψ，表示为

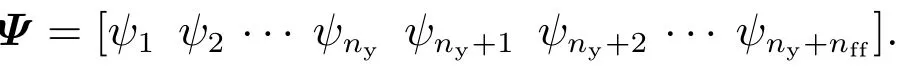
类似地，将参数向量θy和θff组合为一个向量θ，同上式表示为

通过引入输入整形滤波器Ky，输入整形后的参考信号ry可以表示为

根据式(2)，可得到如下条件:

由式(3)可推得，ry与r在平稳段相等，而在移动段有一段延迟，延迟长度等于Ky中基函数的个数.因此，在平稳段，e=r-y=ry-y=ey.若只需要在平稳段的跟踪误差最小，控制性能的评判标准可表示为

最优化的θff和θy需要满足如下定义:

定义2前馈控制器和输入整形滤波器参数向量是最优的，如果在控制系统中引入使用相应参数向量建立的前馈控制器和输入整形滤波器测得的误差信号满足其中S=(I +PC)-1是系统敏感度函数.

建立参数化前馈控制器Kff(θff)和输入整形滤波器Ky(θy)，通过最优化迭代调参算法，算法收敛时可以得到满足定义2的最优参数向量θ*和相应的的和此时Vy(θk)达到最小值.详细算法将在下节中给出.

3 算法设计

3.1 最优化迭代前馈调参算法

根据第2.2节建立的参数化前馈控制器和输入整形滤波器，在图2中，第k次迭代测得的信号和uk可以使用第k次迭代的参数向量θk扩展为参数化形式，表示如下:

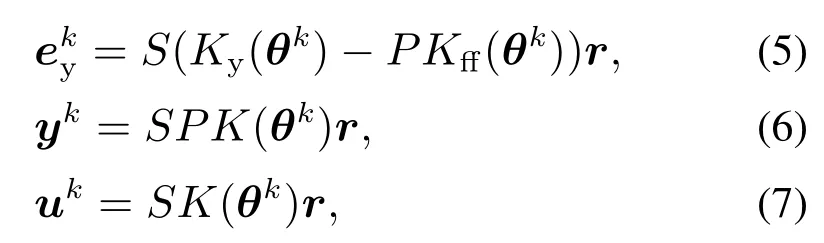
式中 K(θk)=Kff(θk)+CKy(θk).

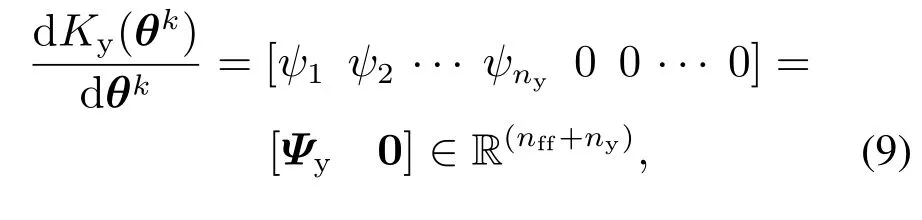
根据式(6)-(7)，通过每次迭代的uk和yk，可以得到S和(SP)的估计值Sest和(SP)est:

假设1K-1(θk)是稳定的.

注1如果K-1(θk)不稳定，可以通过使用文献[25]中的稳定求逆算法计算得到K-1(θk).

将式(9)-(12)代入式(8)中，得到梯度向量的估计值:

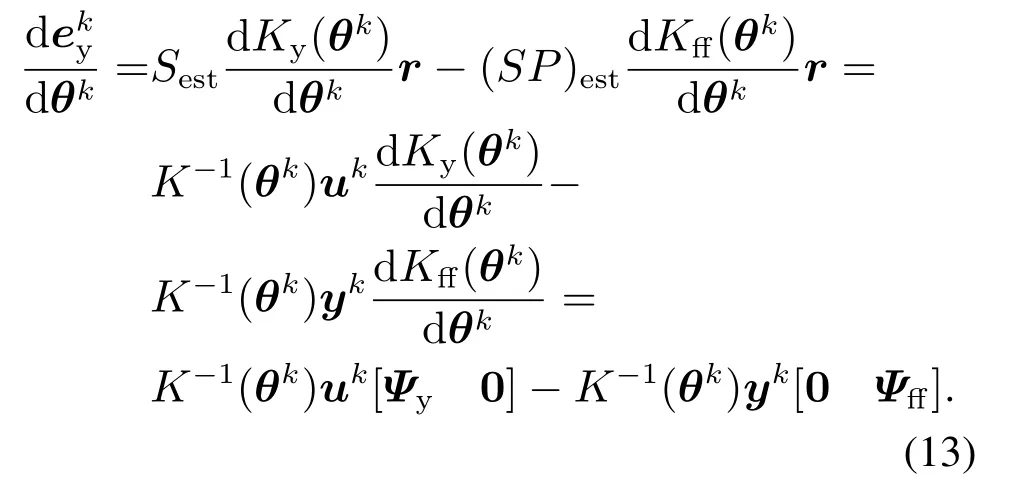
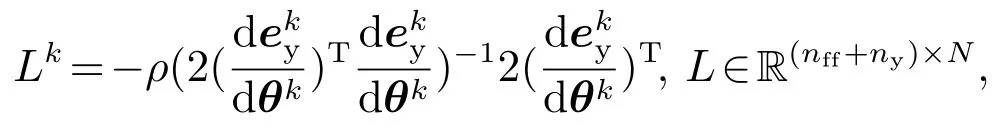
其中ρ为学习增益.设置学习律为

根据以上计算，通过梯度下降法迭代求解最优化问题(13)的步骤可以概括如下:

程序1迭代估计θk.

初始化:

1) 确定合适的学习增益ρ，0 ＜ρ ＜1，使算法在收敛速度和噪声容忍度中取得平衡;

2) 选择合适的基函数Ψ，用于建立参数化前馈控制器Kff，输入整形滤波器Ky和参考信号r;

3) 确定合适的参数向量初始值θ0;

主程序:

1) 使用参数向量θk运行控制程序，获得uk和yk;

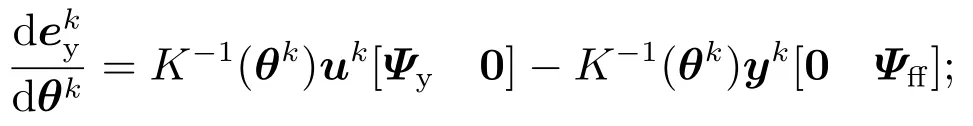
3) 计算学习矩阵

4) 计算下一次迭代的θk+1=θk+Lkek;

5) k →k+1.返回步骤1.

注2通过程序1，根据梯度下降法的收敛性，可以得到一个收敛的参数向量θ，且这个参数向量满足定义1，收敛性证明详见文献[24，26].将这个收敛的参数向量记作θ*.

3.2 通过迭代前馈调参得到前馈控制器

注意到，误差ey是整形参考信号ry与输出信号y之间的差值，并不是跟踪期望轨迹r得到的跟踪误差.因此，最小化的Vy(θk)并不意味着对整个期望轨迹的V(θk)的最小化.

由式(5)，可以得出，误差ey等于0的条件为

由式(14)，可以得到如下结论:建立Kff和Ky是为了得到系统逆模型的估计值，使ey为0.如果建立的Kff和Ky使ey为0，此时就可以作为系统逆模型的估计值.这与文献[22]中的迭代学习系统辨识概念类似.由梯度下降法的最优性，当使用梯度下降法的程序1收敛时，可认为结果满足定义2，即=0.此时由收敛时的组合成的可以作为系统逆模型的估计值.因此在控制结构中引入KIFT=作为前馈控制器.

在Kff和Ky收敛为后，移除原本的前馈控制器Kff和输入整形滤波器Ky，将KIFT=作为前馈控制器加入到系统中，补偿期望轨迹引入的扰动.KIFT输出的前馈控制量uIFT为

注3如果不稳定，可以通过零相位跟踪技术[31]得到稳定的KIFT.

使用组合的KIFT=而不是直接使用作为前馈控制器，是因为单独的Kff只能估计系统传递函数的分母部分，无法准确估计系统逆模型[24].而不直接将Kff参数化为分子和分母都为多项式的形式，即文献[29]中的有理基函数:

是因为对有理基函数参数化的Krat进行最优化迭代运算时，算法复杂度高，且需要选择合适的使算法收敛的权重矩阵，而这个矩阵是N×N维[29]或N×n维的[30]，维度高导致待定参数过多，难以选择使算法收敛的参数矩阵.而将Krat分解为本文的Kff和Ky，不需要设置高维权重参数矩阵进行，显著降低了算法复杂度，同时保证算法效果.

3.3 迭代前馈调参与迭代学习控制结合算法

对比ILC与IFT，发现IFT鲁棒性很强，期望轨迹变化时控制效果依然稳定，而ILC在变轨迹时存在严重的效果恶化现象;然而，ILC经过几次学习就可以达到比IFT更高的控制精度，这是由于ILC还去除了KIFT无法消除的其他重复性扰动.

仅使用第3.2节中获得的最优前馈控制器KIFT得到的控制精度较低.为了提高控制精度，引入迭代学习控制器KILC，采集上一个迭代周期的误差ek-1，离线更新前馈控制量消除其他重复性扰动.在本文中，选用PD型迭代学习控制器，第k次迭代时KILC输出的前馈控制量为

其中kp和kd为学习律的学习参数.

根据上文所述的最优化梯度下降迭代前馈调参方法，得到前馈控制器KIFT，并与PD型迭代学习控制结合，可以将完整算法流程图表示如图3.算法的具体步骤表示如程序2.

图3 本文提出算法的流程图Fig.3 Flow chart of proposed algorithm

程序2

1) 运行程序1，获得收敛的最优参数向量θ*;

2) 移除Kff和Ky;

3) 建立KIFT=

4) 在控制结构中加入KIFT和KILC;

5) 根据新的控制结构进行实验，直到满足停止条件.

注4由于算法只是预先消除了由期望轨迹引入的误差，对迭代过程没有影响，因此稳定性与PD型迭代学习律的稳定性相同.证明详见文献[14].

4 迭代前馈调参仿真

在本段中，对结合前馈调参与迭代学习的算法进行仿真，验证算法的有效性.

仿真使用的离散传递函数模型如下:

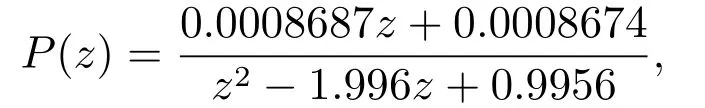
其中采样时间为Ts=1×10-4s.仿真中采用Kp=1.05，Kd=25的PD型反馈控制器，可以写作

在系统中加入扰动μ，它的模型为μ=Hϵ，其中:

ϵ是标准差为1×10-7的零均值白噪声.

仿真使用的传递函数的频率响应如图4(a)中实线所示.根据图中的频率响应，可以看出系统主要动态特性集中在0.1～100 Hz的频段，而Kff和Ky的引入是为了补偿系统的主要动态特性.系统使用5阶点到点的期望轨迹r.

根据对仿真模型的分析和第2.2 节中定义1，建立Kff(θff)和Ky(θy)如下:

对于参数向量θ，设置初始值为

设置学习增益ρ为0.9，使用以上的Kff和Ky，运行程序1.对运行结果作图:图4(a)为对第2次迭代的Kff和Ky分别作出频率响应，与传递函数P进行对比的图形;图4(b)为θk随迭代次数的变化;图4(c)为第2次迭代的与P的对比图.分析运行结果，可得出以下结论:

1) 通过图4(a)看出，算法收敛时，单独的Kff和Ky都不足以描述系统的动态特性;

2) 由图4(b)可以看出，程序在第2次运行后θk变化很小，说明调参算法收敛速度快，且可以将第3次迭代的结果看作算法收敛时得到的最优值.此外，还可以通过调整学习增益ρ来调整算法的收敛速度;

图4(a) 仿真中算法收敛时Ky，Kff与P的伯德图Fig.4(a) Simulation bode diagram of converged Ky and Kffcompared with P

图4(b) θ随迭代次数变化的仿真结果Fig.4(b) Simulation result of θ during iteration

图4(c) 仿真中算法收敛时Ky(Kff)-1与P的伯德图Fig.4(c) Simulation bode diagram of converged Ky(Kff)-1 compared with P

5 实验

在本章中，笔者将提出的控制方法在实验平台上进行测试，验证算法的有效性.

5.1 实验平台

本文使用如图5(a)所示的直线伺服控制平台.实验伺服系统由上位机PC机，POWER PMAC控制卡，AMAC驱动器和NEWPORT IDL225直线电机运动平台组成.直线电机的位移由Heidenhain增量式编码器测量，分辨率为20 μm，然后通过插值得到10 nm的分辨率.电机由数字伺服驱动器驱动.算法使用C语言在PowerPmac控制器中进行实现.系统的采样周期为Ts=0.0001 s.

使用扫频法获得实验平台的频率响应如图5(b)所示.为了验证算法，规划了如图5(c)的两种5阶点到点期望轨迹r1和r2，每个期望轨迹由N=2000个点组成.实验中，使用线性PD型反馈控制器，表示为Cpd=其中:Kp=1.05，Kd=25.

图5(a) 直线伺服控制实验平台Fig.5(a) Photograph of experimental platform

图5(b) 实验平台的频率响应图Fig.5(b) Frequency response of experimental platform

图5(c) 实验使用的两种期望轨迹和速度、加速度示意图Fig.5(c) Two different reference trajectorys with their velocity and acceleration

5.2 输入整形迭代前馈调参

如前文所述，最优化的Kff(θ*)和Ky(θ*)需要估计系统主要频段的动态特性.根据图5(b)中的频率响应图，系统主要频段为0.1～100 Hz.基函数选择为

使用图5(c)中的r1作为期望轨迹，在实验平台上运行程序1，测量每次迭代的θ和误差并记录.为了说明收敛情况，对建立Kff的4个参数作图如图6(a).可以看出，θ在第2次迭代后波动很小，可以认为参数向量在第2次迭代时收敛，算法收敛速度快，因此对程序2的运行时间影响不大.

为了验证IFT的控制精度，记录每次迭代的Vk，并作图如图6(b).可以发现，第2次迭代之后，V 的波动很小，这也与仿真相符.通过IFT，轨迹跟踪的误差平方和V 减小了两个数量级，说明IFT可以对期望轨迹引入的扰动进行一定的补偿，提高控制精度.算法收敛时得到的平稳段误差信号如图6(c)所示，其中1ct=10 nm.

图6(a) 参数向量随迭代次数的变化情况Fig.6(a) Result of θ during iteration

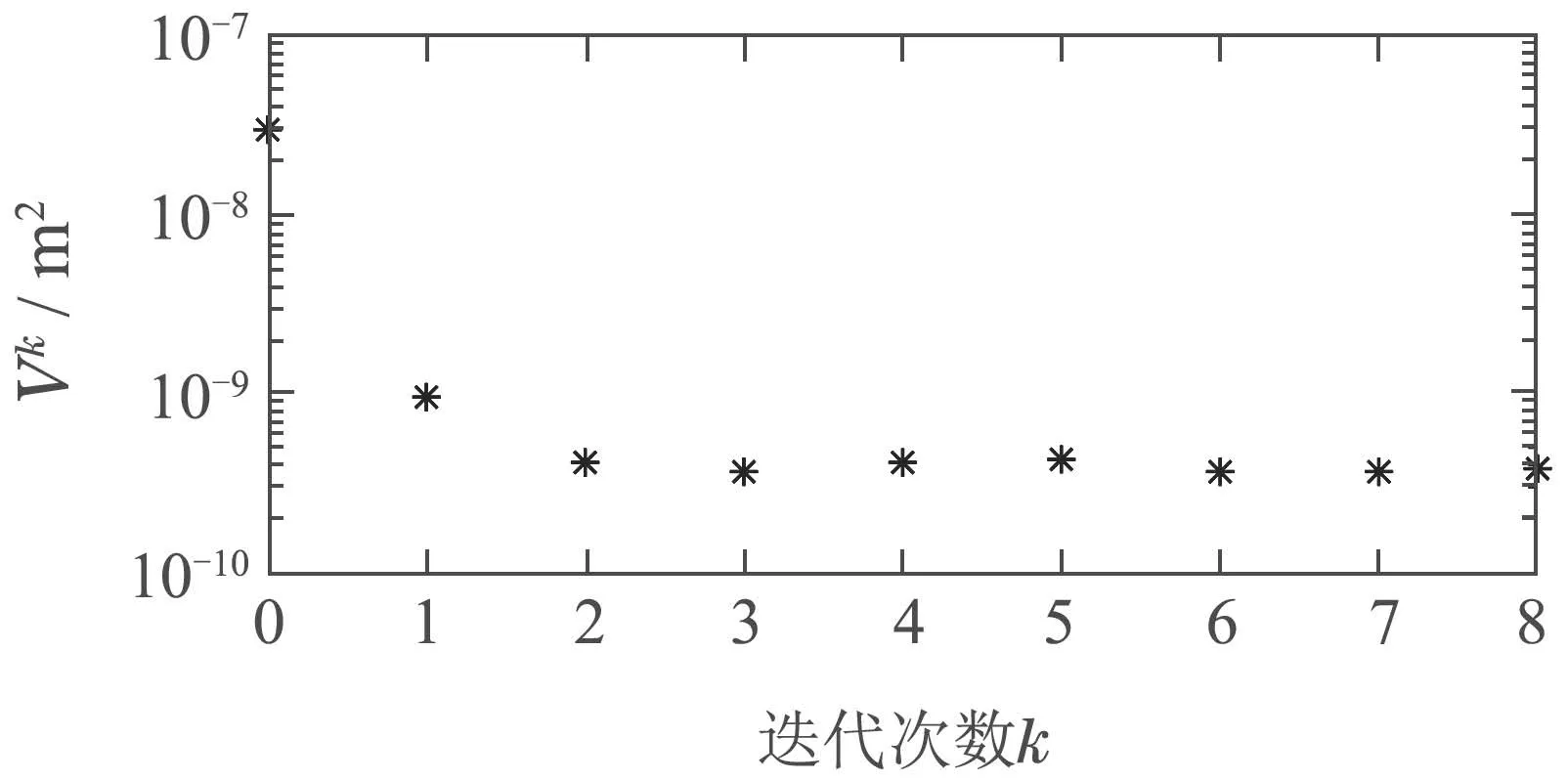
图6(b) 迭代前馈调参得到的Vk随迭代次数k的变化情况Fig.6(b) Vk achieved from IFT

图6(c) 迭代前馈调参得到的平稳段误差信号Fig.6(c) Error signal during dwell period achieved from IFT

5.3 本文提出的IFT-ILC算法

为了得到最优前馈控制器KIFT，需要计算KIFT=并希望它描述系统主要频段的动态特性.由第5.2节的实验结果，使用第2次迭代得到的参数向量作为最优参数向量θ*，建立KIFT=Kff(θ*)·(Ky(θ*))-1.将系统频率响应与KIFT的幅频特性作比较，并同时作出Kff和Ky的幅频特性，如图7(a).图中:灰实线为系统幅频特性，黑实线为KIFT的幅频特性，虚线为Ky，点线为Kff.从图中可以看出，KIFT可以在主要频段描述系统动态特性，而单独的Kff(θ*)和Ky(θ*)都不足以描述系统.因此选用KIFT作为系统前馈控制器是合适的.

图7(b)显示了仅加入最优前馈控制器的算法与本文提出算法的V 随迭代次数变化情况的对比，期望轨迹为r1.由图中结果可以看出，仅使用KIFT作为前馈控制器的算法在第1 次迭代后，Vk由不加前馈时的2.5×10-8m2降低到了7.5×10-10m2，之后的10次迭代中Vk不再有显著的下降;而使用本文提出的IFT与ILC相结合的算法，在第1次迭代后效果与仅使用KIFT时相同，但之后的10次迭代中Vk仍随着迭代逐渐下降，在第10次迭代后Vk降低到3.4×10-11m2.可见期望轨迹不变时，本文提出的算法精度远高于无学习的精度.

为了验证算法在轨迹变化时的效果，在第5次迭代后将期望轨迹由r1变为r2，对ILC和本文提出的IFTILC算法进行实验，记录Vk的变化情况如图7(c).期望轨迹变化时，PD型迭代学习控制的Vk由1.8×10-10m2变为6.2×10-9m2，发生了严重的效果恶化，而使用本文提出的算法，在期望轨迹变化时，Vk为1.2×10-9m2，效果恶化得到减轻.可见，在期望轨迹发生变化时，仅使用PD型学习律的ILC的控制效果恶化十分严重，而本文提出的算法能减轻效果恶化，提高控制的鲁棒性.

图7(a) 实验平台频率响应与，和KIFT的伯德图Fig.7(a) Frequency response of experimental platform，，and KIFT

图7(b) 迭代前馈调参与本文算法的Vk的对比图Fig.7(b) Comparison of Vk of IFT with proposed algorithm

图7(c) 期望轨迹发生变化时迭代学习控制与本文算法的Vk的对比图Fig.7(c) Comparison of Vk of ILC with proposed algorithm when reference signal changes

6 结论

为了改善变轨迹控制任务中ILC的效果恶化问题，同时保证高控制精度，本文提出了一种结合输入整形滤波器，迭代前馈调参与迭代学习控制的数据驱动控制算法.算法是数据驱动的，不需要已知模型信息，而是使用输入输出数据，通过迭代前馈调参在算法运行过程中对模型进行估计.在迭代前馈调参过程中，使用基函数对控制器进行参数化，并使用梯度下降法进行参数优化，从而获得最优前馈控制器;输入整形滤波器的引入在保证模型估计精度的同时简化了计算.最优前馈控制器对期望轨迹引入误差进行补偿，减轻了轨迹变化带来的效果恶化，而迭代学习控制的引入保证了控制精度.为了验证算法的有效性，本文将提出的算法应用到直线电机系统中，并与现有算法进行了对比，实验结果表明本算法能够更好的处理变轨迹的轨迹跟踪问题.