圆锥曲线的几何性质

一、填空题

1.抛物线y=4ax2（a≠0）的焦点坐标是_________.

3.经过点A（3，-1），且对称轴都在坐标轴上的等轴双曲线方程为________.

4.设F1，F2分别是椭圆C：（a＞b＞0）的左、右焦点，M是C上一点且MF2与x轴垂直，若直线MF1的斜率为，则椭圆C的离心率为________.

5.已知F1，F2分别是椭圆的左、右焦点，P是椭圆上的任意一点，则的取值范围为________.

6.已知P是抛物线y2=2x上动点，，若点P到y轴的距离为d1，点P到点A的距离为d2，则d1+d2的最小值是________.

7.在平面直角坐标系xOy中，P为双曲线x2-y2=1右支上的一个动点.若点P到直线x-y+1=0的距离大于c恒成立，则实数c的最大值为________.

8.已知椭圆C：的左焦点为F，若F关于直线的对称点A是椭圆C上的点，则椭圆C的离心率为________.

二、解答题

（1）求此双曲线的方程；

（2）设P为双曲线上一点，A，B两点在双曲线的渐近线上，且分别位于第一、二象限，若，求△AOB的面积.

10.如图，A，B是椭圆C：（a＞b＞0）的左、右顶点，M是椭圆上异于A，B的任意一点，直线l是椭圆的右准线.

（1）若椭圆C的离心率为，直线l：x=4，求椭圆C的方程；

（2）设直线AM交l于点P，以MP为直径的圆交MB于Q，若直线PQ恰好过原点，求椭圆C的离心率.

11.已知抛物线C：x2=-2py经过点（2，-1）.

（1）求抛物线C的方程及其准线方程；

（2）设O为原点，过抛物线C的焦点作斜率不为0的直线l交抛物线C于两点M，N，直线y=-1分别交直线OM，ON于点A和点B.求证：以AB为直径的圆经过y轴上的两个定点.

12.已知斜率为k的直线l与椭圆C：交于A，B两点，线段AB的中点为M（1，m）（m＞0）.

（2）设F为C的右焦点，P为C上一点，且成等差数列，并求该数列的公差.

三、挑战高考（2014年江苏卷第17题）

13.如图，在平面直角坐标系xOy中，F1，F2分别是椭圆=1（a＞b＞0）的左、右焦点，顶点B的坐标为（0，b），连接BF2并延长交椭圆于点A，过点A作x轴的垂线交椭圆于另一点C，连接F1C.

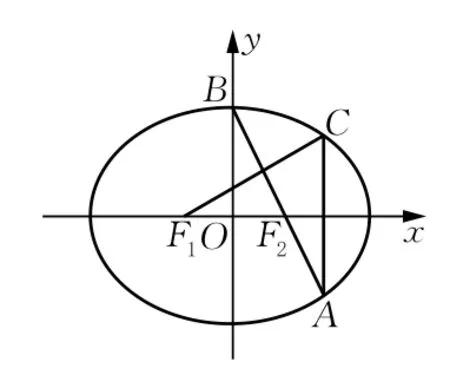
（第13题）

（1）若点C的坐标为，且BF2，求椭圆的方程；

（2）若F1C⊥AB，求椭圆离心率e的值.