微灌石英砂颗粒表面滞纳能力计算与分析

2020-07-15刘清霞翟国亮李景海李国强

节水灌溉 2020年7期

刘清霞，翟国亮，李景海，李国强，邓忠

(1.安阳工学院土木与建筑工程学院，河南安阳 455000；2.中国农业科学院农田灌溉研究所，河南新乡 453002；3.安阳市一中数学组，河南安阳 455000)

0 引言

微灌砂过滤器在对水的过滤过程中，砂滤料会与水中杂质频繁接触。而由于砂颗粒表面粗糙度的存在，砂颗粒在与水中杂质接触过程中会对水中杂质产生一定的滞纳作用。砂颗粒表面对杂质的滞纳能力，直接影响砂滤层过滤过程的水头损失和过滤效果。砂过滤器滤料颗粒表面滞纳机理分析与滞纳能力的研究，对于砂过滤器的运行和砂滤料的选型具有十分重要的意义。

而目前，在砂滤层过滤机理方面的研究，主要侧重于宏观定性分析，董文楚等[1]认为，砂滤层的过滤方式主要是机械过滤，而机械过滤主要体现在砂滤层的筛子作用、沉淀作用和接触凝絮作用。Wenquan Niu[2]等对砂滤层物理堵塞开展了相关研究；翟国亮等[3]用砂滤层对粉煤灰水进行过滤，分析了滤后水浊度的变化规律；Bové等[4,5]研制了一种适用于砂过滤器的滤帽，并采用数值模拟的方法对过滤器水头损失进行了研究；李景海等[6-8]通过建立数学模型，对砂滤层最佳过滤速度进行了探讨。

砂颗粒表面的粗糙程度对过滤效果的影响，目前尚没有进行深入分析。而在其他领域，如植物叶片对空气中颗粒物滞纳能力的研究，有不少相关报道。王赞红等[9]对城市街道常绿灌木植物叶片滞尘能力及滞尘颗粒物形态进行了研究。王蕾等[10,11]对北京市六种针叶树叶面附着颗粒物的理化特征进行了分析，并分析了北京市春季天气状况对针叶树叶面颗粒物附着密度的影响。王会霞等[12]分析了城市绿化植物叶片表面特征对滞尘能力的影响。刘璐等[13]对广州市常见行道树种叶片表面形态与滞尘能力进行了分析。杨志丹等[14]以毛白杨叶片为例探讨了植物叶片吸滞 PM2.5等大气颗粒物定量研究方法。房瑶瑶等[15]研究了叶片表面粗糙度对颗粒物滞纳能力的影响。刘一超等[16]研究了北京通州不同树种滞纳大气颗粒物的能力。赵文君等[17]研究了贵阳市木兰科树种叶片滞尘效应及影响因素。

在前期研究的基础上[18,19]，借鉴前人研究成果，笔者选取3种微灌石英砂滤料的砂颗粒作为样本，对石英砂颗粒表面对过滤水中杂质颗粒的滞纳能力进行分析。首先采用三维表面形貌仪对砂颗粒表面最大轮廓峰高与最大轮廓谷深之和，即轮廓最大高度进行测量，并对轮廓最大高度对应的波纹宽度进行测量，在此基础上，对砂颗粒滞纳水中杂质颗粒的机理进行分析，并计算砂颗粒对水中杂质颗粒的滞纳能力。

1 微灌石英砂颗粒表面形貌参数

石英砂颗粒表面轮廓是平面与砂颗粒实际表面相交所得的轮廓。颗粒表面轮廓算术平均偏差Sa是颗粒表面粗糙度最主要的评定参数，表征砂颗粒表面起伏的平均高度，表达式为：

(1)

式中：Sa为表面轮廓算术平均偏差，μm；A为测量表面的面积，μm2；z为测量表面上点(x,y)的高度，μm。

砂颗粒表面轮廓单元最大宽度Ss，指轮廓单峰间距的最大值。该参数决定了砂颗粒表面所能滞纳的最大杂质颗粒的粒径。如图1所示0～1之间的距离即为表面轮廓单元最大宽度Ss。

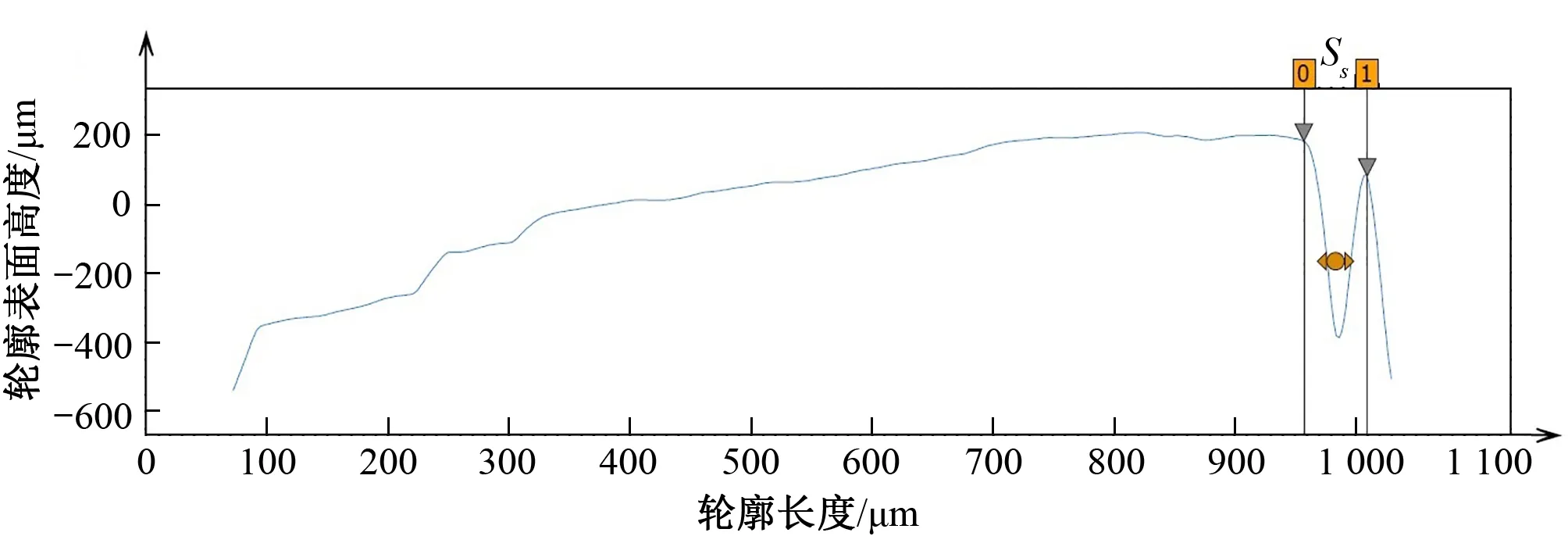
图1 表面轮廓单元最大宽度示例Fig.1 Example of maximum width of surface profile unit

2 微灌砂颗粒表面形貌参数的测算

以粒径范围为1.0～1.18 、1.18～1.4和1.4～1.7 mm的3种滤料的砂颗粒为研究对象，每种滤层中各随机取15粒石英砂作为样本，采用型号为ST400的三维表面形貌仪(图2)对砂颗粒扫描。得到砂颗粒表面轮廓算术平均偏差Sa。表面轮廓单元最大宽度Ss则在表面轮廓线上测量得到。砂颗粒表面形貌参数结果见表1。

图2 三维表面形貌仪Fig.2 Three dimensional surface profiler

表1 砂颗粒表面形貌参数测算结果 μmTab.1 Calculation results of surface morphology parameters of sand particles

3 微灌砂颗粒表面滞纳能力分析

3.1 砂颗粒表面滞纳杂质颗粒机理分析

当水流通过砂滤层时，由于砂颗粒处于静止状态，而水流具有一定流速。因此，由滤层孔隙中心到砂颗粒表面，水流存在一个由最大值到静止的渐变边界层，在该渐变边界层内，水流速度较低，水流处于层流状态。水中杂质颗粒在滤层孔隙内湍流作用下，部分颗粒会向边界层移动，当移动到边界层时，由于水流速度降低，杂质颗粒则会缓慢地附着到砂颗粒表面。若砂颗粒表面比较光滑，则杂质颗粒在水流的作用下，会继续向前运动。若砂颗粒表面存在明显的凹凸时，较细的杂质颗粒会在水流侧压作用下嵌入到砂颗粒表面的凹处，从而逐渐在砂颗粒表面聚集，使砂颗粒表面形成一个由杂质细颗粒组成的壁面。由于细小杂质颗粒之间吸附力的作用，杂质颗粒间的内摩擦力一般比杂质颗粒与砂颗粒间的摩擦力大[20]，后面的颗粒会继续附着在紧贴砂颗粒表面的那层细小颗粒上，细小颗粒的不断附着，导致砂颗粒表面滞纳区的形成。

砂颗粒表面滞纳区在形成过程中，首先停留到砂颗粒表面的杂质颗粒粒径较大，而后较细小的杂质颗粒继续附着上去。当表面滞纳区达到一定厚度时，在重力和水流带动作用下，滞纳区会整体向下推移，滞纳区边缘的细小颗粒会被水流带走，杂质颗粒的聚集与下移形成一个动态的平衡过程。

3.2 砂颗粒表面滞纳杂质颗粒粒径计算与分析

由砂颗粒表面滞纳区形成机理可知，表面滞纳区形成的关键是要有一部分细小的杂质颗粒能停留在砂颗粒表面，这主要取决于砂颗粒表面平均起伏高度、砂颗粒表面轮廓单元最大宽度和杂质颗粒的粒径等因素[21]。在砂颗粒表面滞纳区形成的决定因素中，砂颗粒表面平均起伏高度可以用颗粒表面轮廓算术平均偏差Sa表示，显然Sa越大，杂质颗粒越容易停留在砂颗粒表面；砂颗粒表面轮廓单元最大宽度Ss越大，则能够停留的杂质颗粒粒径越大。

将砂颗粒表面轮廓的一个单元简化为一个锯齿形，将杂质颗粒近似为圆球体来处理，则可以对砂颗粒表面凹凸处所附着的杂质颗粒进行受力分析，见图3。图3中，Ff为浮力，mg为重力。

由于颗粒表面轮廓算术平均偏差Sa表示砂颗粒表面的平均起伏高度，因此，在砂颗粒表面凹处和凸处的平均高度都为Sa，而表面轮廓单元最大宽度Ss即为锯齿的开口宽度，设θ为锯齿顶角的半角。

在图3中，杂质颗粒在锯齿口所受静摩擦力为：

Fm=(mg-Ff)cosθμ

(2)

式中：Fm为静摩擦力，N；μ为最大静摩擦系数，无量纲；其余同上。

使杂质颗粒向下脱落的力为：

Fh=(mg-Ff)sinθ

(3)

使杂质颗粒不脱落的条件是：

Fm≥Fh

(4)

(mg-Ff)cosθμ≥(mg-Ff)sinθ

(5)

将式(5)化简，得：

μ≥tgθ

(6)

假设杂质颗粒为细砂颗粒，而砂颗粒之间的内摩擦角为28°～36°，若砂颗粒之间最大静摩擦角取28°，则最大静摩擦系数为：

μ=tg 28°=0.532

(7)

由公式(6)、(7)知，当θ不大于28°，即tgθ不大于0.532时，杂质颗粒能够较稳定的嵌入到砂滤料的凹处。根据直角三角形边角关系，有：

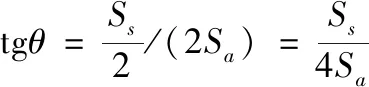
(8)

将tgθ用可嵌入砂滤料凹处的最大杂质颗粒半径表示，得：

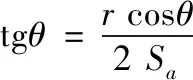
(9)

式中：r为可嵌入砂滤料凹处的最大杂质颗粒半径，μm。

由公式(8)、(9)得：

(10)

式中：d为可嵌入砂滤料凹处的最大杂质颗粒直径，μm。

根据式(10)，可以得到砂颗粒所能滞纳的最大杂质颗粒粒径(表2)，采用样本参数的均值、标准差和变异系数对计算结果进行统计分析。

表2 砂颗粒表面滞纳杂质颗粒最大粒径计算结果Tab.2 Calculation results of the maximum particle size of the stagnant impurity particles on the surface of the sand particles

(11)

式中：xi为样本参数。

样本标准差s为：

(12)

样本变异系数Cv为：

(13)

由表2知，3种滤料的砂颗粒表面轮廓单元tgθ的最大值分别为0.429、0.301和0.381，均小于tg28°，说明杂质颗粒能够较稳定的嵌入到砂滤料的最大凹处。而可嵌入砂滤料凹处的最大杂质颗粒直径分别为110.5、90.5和132.5 μm，可嵌入砂滤料凹处的最大杂质颗粒直径的均值分别为67.5、64.4和58.3 μm。3种滤料可滞纳杂质颗粒最大直径的标准差分别为27.6、16.5和19.1 μm，标准差代表了杂质颗粒直径在均值上下的波动幅度。杂质颗粒直径变异系数分别为0.401、0.257和0.335，与标准差具有相同的变化规律。可见，粒径为1.18～1.40和1.40～1.70 mm砂滤料可嵌入杂质颗粒直径波动幅度相对较小且比较接近，而粒径为1.00～1.18 mm的砂滤料杂质颗粒直径波动幅度较大，原因在于，小颗粒的石英砂在加工时，表面的粗糙度不易控制，会出现表面粗糙度不均匀的现象，而颗粒较大的石英砂表面粗糙度则较容易控制。

综上可知，粒径为1.18～1.40和1.40～1.70 mm砂滤料，过滤性能相对稳定，而粒径为1.00～1.18 mm的砂滤料过滤性能的稳定性则较差，因此，在选取砂滤料方面，应适当增加砂滤料的粒径，以提高砂滤层过滤性能的稳定性。