广西山丘坡地土壤墒情时空变异特征及时间稳定性分析

2020-07-15查元源吴卫熊史良胜

节水灌溉 2020年7期

黄凯，查元源，吴卫熊，史良胜

(1.广西水利科学研究院，南宁 530023；2.武汉大学水利水电学院，武汉 430072;3. 广西水工程重点实验室，南宁 530023)

土壤根系墒情是土壤-植物-大气连续体系统中“四水转化”的关键因子，控制着地表径流、雨水入渗、土壤蒸发、植被蒸腾等一系列生态和水文过程，受到土壤质地、地形、微气候、植被等空间分布不均因素的影响，可能具有较强的时空变异性[1-3]。广西具有丰富的光热资源，经济作物产业发达，土地利用程度较高，山丘坡地是广西耕地的重要类型[4]。由于地形和土壤质地的空间变化，广西山丘坡地的土壤墒情呈现强烈的空间变异性[5]。广西属于亚热带季风气候，雨量充沛，蒸散发强烈，造成土壤墒情干湿剧烈交替变化，可能出现季节性干旱或渍害，影响作物产量。虽然安装土壤墒情传感器可以采集不同时间、不同深度的土壤含水量，但其空间代表性较差，无法等同于大田管理尺度平均的根区土壤含水量，给灌溉排水管理带来了困难。广西等喀斯特地区土壤墒情研究还处于探索阶段，已有研究主要从生态学出发，侧重对大尺度土壤墒情时空变异的统计研究[6,7]，得到了不同深度和不同坡度土壤含水量的空间变异特征[8,9]，但从农业管理角度出发的田间管理尺度土壤墒情时空变异研究较少，尤其是大于20 cm深度的土壤墒情，由于观测成本限制，尚未见相关研究报道。本文在前人对土壤墒情时空变异研究的基础上，拟分析广西崇左60个试验小区2017年采集的0～80 cm深度土壤含水量数据，分析其时空变异性及影响因素，并采用土壤含水量时间稳定分析方法[10]确定试验小区代表性土壤墒情观测点位置，为后续土壤墒情便捷管理提供代表性观测数据。

1 研究区与数据

1.1 研究区概况

研究区位于广西壮族自治区西南崇左市江州区，经纬度为22.31°N, 107.23°E，海拔高度180 m。试验站所在地为典型喀斯特地貌，属热带季风气候，气候温暖湿润，年平均降水约为1 300 mm，年平均气温22 ℃。试验区共设有60个小区(图1)，单个小区面积为64 m2(8×8 m2)，相邻小区间隔约为2 m，种植糖料蔗，种植时间为2017年3月1日至2017年12月23日，共298 d。小区仅对0～40 cm土壤进行简单翻耕，因此耕地仍有较大的地形起伏(高程175～180 m，类似马鞍型，见图1)和土壤质地空间变异。根据土壤质地分析，试验小区0～40 cm的土壤为粉黏土，40 cm以下为黏土，有较多的铁锰结核，双套环试验显示其渗透性能强，土壤保水性较差。

图1 试验小区总体布置(修改自文献[11])Fig.1 The plan view of the experimental plots (adopted from reference[11])

1.2 观测数据

试验阶段主要进行地面数据观测及无人机遥感数据观测，其中地面观测包括土壤颗粒分析、双套环入渗分析和土壤墒情测定。通过无人机遥感平台并计算可获得地形图[11]。

1.2.1 无人机遥感平台观测

试验采用八旋翼无人机(DJI S1000)，搭载SONY DSC-QX100 数码相机。数码相机传感器尺寸为13.2 mm×8.8 mm，像素为2020万，镜头焦距10.4 mm。利用Agisoft PhotoScan Professional 以及Eris Arcmap软件对RGB照片进行处理并计算地形高度，生成地形图(图1)。

1.2.2 气象、蒸发数据

气象站采用watchdog-2000系列气象站自动监测，监测时间间隔为1 h，监测项目包括气压、太阳辐射、空气相对湿度、温度、降雨、风向、最大风速、平均风速、露点温度。

蒸发站包括水面蒸发、土壤蒸发，水面蒸发采用自动监测蒸发站，土壤蒸发采用自制称重式株间蒸发站。

自2017年1月初至2017年12月底，该气象站共进行监测350 d，每日降雨及根据彭曼-蒙特斯公式计算的参考作物腾发量如图2所示。崇左2017年降雨总量为1 280 mm，属于平水年，图2所示降雨蒸散发呈现夏多冬少、年度分配不均的特点，符合广西亚热带季风气候特征。

1.2.3 土壤物理性质

通过分层取样分析，获取了试验地土壤砂粒、粉粒和黏粒含量，确定其0～40 cm土壤质地为粉黏土，40 cm以下为黏土。0～40 cm土壤松软，其容重在1.1～1.2之间；40 cm以下容重为1.3～1.4之间。由于土壤铁锰含量高，土壤中有较多肉眼可见的铁锰结核，造成了土壤质地的空间变异。

1.2.4 土壤墒情数据

土壤墒情数据采用FDR-TRIM管测量，设计测量时间间隔为3～10 d，测量6个深度，分别为地下10、20、30、40、60、80 cm。每个小区不同水平位置设1～3个预埋管，共计92个。FDR-TRIM需要人工将仪器伸入预埋管测量，自2017年3月1日至2017年12月10日，共监测土壤墒情41次，平均每7 d一次，原预计获取41×6×92=22 632 个土壤含水量数据，但测量中因超过一半预埋管损坏而未测，实际取得有效数据为9 863 个。FDR-TRIM测量的数据均通过烘干法进行了标定，并根据容重转化为土壤体积含水量，因此本文中的土壤墒情指标定后的FDR-TRIM体积含水量数据。

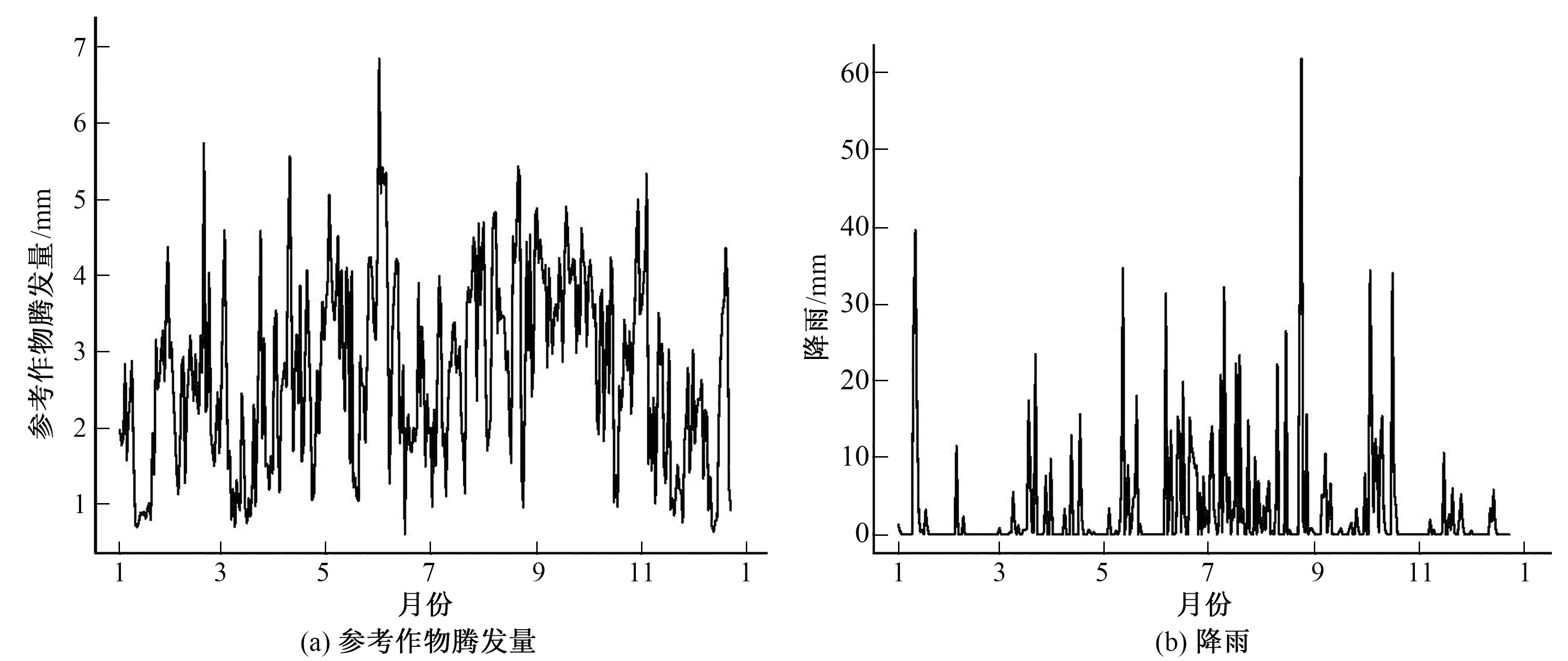
图2 2017年试验站观测的降雨及由彭曼-蒙特斯公式计算的参考作物腾发量Fig.2 Observed precipitation and the reference evapotranspiration calculated based on Penman-Monteith equation at the experimental site in year 2017

2 研究方法

本文以2017年获取的试验地不同水平地点、不同深度的土壤墒情时间序列数据为研究对象，采用地统计学与时间序列分析方法得到了土壤墒情的时空变异特点，并试图根据土壤质地、地形等空间变异因素和气象条件等时间变异因素解释土壤墒情时空变异性的形成原因。

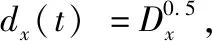
其次，我们采用地统计学分析土壤墒情在水平方向的变异性，得到变异函数拟合的方差和相关长度，采用条件模拟得到不同深度的时间平均土壤含水量等值线图Et(x)，最后分析地形指标和墒情的相关关系。在垂向上也单独分析了土壤墒情剖面的变异特征。

再次，分析了不同深度的水平方向平均土壤含水量Exy(z,t)随时间的变化规律，并与气象条件进行了对比，分析作物是否受到水分胁迫。

最后，我们采用时间稳定性分析比较了不同观测点在反映整个试验地平均墒情方面的代表性。时间稳定性指在不同测量时间下，土壤含水量呈现较一致性的空间变化样式，而恰好有些样点在任何测次下都能很好地代表整个研究区的平均土壤墒情[12]。将所有空间测点的土壤含水量按高低排序，这些样点的顺序在不同测次基本没有变化或变化不大。这种土壤墒情空间样式的时间不变性定义为时间稳定性。一些研究学者运用时间稳定性分析方法证实了优选测点位置确实可以很好地表征小流域的平均土壤墒情[13]。

3 结果与分析

3.1 土壤墒情时空变异总体特征

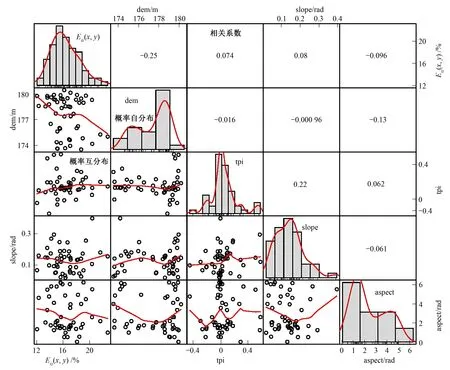
图3(a)中显示了空间平均土壤含水量Ex(t)(共计92位置和6个深度，即对一次测量时间的不同点土壤含水量取空间平均)与对应标准差dx(t)的关系图。可以看出对于不同时间t，该试验地空间平均含水率Ex(t)在21%到30%之间波动，其空间标准差dx(t)在7%到13%之间，空间均值和空间标准差之间无明显相关性；空间变异系数(CV=d/E)在0.30～0.55之间[图3(b)]，属于中等变异(10%

图3(c)中显示了土壤含水率、量数据在时间坐标方向的平均值(共计41个观测时间，即对特定三维空间坐标测点的所有时间土壤含水率数据进行平均)。在不同位置x，该试验地时间平均含水量Et(x)在10%到60%之间波动，其时间平均含水量的标准差dt(x)在1%到30%之间，Et(x)和dt(x)之间呈现弱正相关性(剔除变异性异常大点)；变异系数在0.01～1.00之间[图3(d)]，时间平均含水量Et(x)与对应变异系数CVt(x)也呈现一定的负相关关系(剔除变异性异常大点)。注意到时间平均含水量的标准差及变异系数大概有十几个点明显偏大。经检查，发现数据集中于60和80 cm深度，不同测次跳动较大，这可能与TRIM伸入预埋管测量时，产生测量深度人为误差有关。

3.2 土壤墒情空间变异分析

以下从水平空间和垂向上分别分析土壤墒情空间变异特征，并分析造成变异的原因以及对田间水分管理的影响。

3.2.1 水平空间土壤墒情

将不同时间获取的土壤含水量进行平均，得到三维空间的时间平均含水量Et(x)。再按照6个不同深度分别进行水平方向的空间变异地统计分析，结果见图4。采用指数型半球变异函数进行拟合，得到6个深度的基台值为4.4、13.35、25.08、33.61、54.79、89.56。对于平稳随机场，拟合基台值代表方差，这说明时间平均土壤含水量Et(x)的水平变异性随着深度呈现增大趋势。相关长度分别为4.31、10.58、8.79、6.74、6.47、11.99 m。因本次取样间距多大于一个小区宽度(8 m)，较大的取样间距使得数据无法体现小尺度的变异性和相关性。

图3 试验田土壤墒情时空均值与变异性关系Fig.3 The relationship between the spatial and temporal mean soil moisture values and their variabilities

图4 不同深度z的时间平均土壤含水量Et(x)水平方向地统计变异函数及拟合模型Fig.4 The variogram data and fitted model in horizontal direction for the temporal averaged soil moisture at different depths

根据拟合变异函数和已有时间平均观测点进行克里金条件模拟，可以得到不同深度土壤时间平均墒情等值线图(图5)。可以看出，土壤时间平均墒情随着深度明显增大。从水平方向的分布来看，0～40 cm深度在研究区域最中心土壤含水量较小，围绕其一圈较大，外部含水量又较小；60和80 cm显示中部地区含水率较大，而边界相对较小。

为了评价土壤墒情水平空间变异性与地形指标的关系，我们首先采用无人机和地面定标获取了地形高程图dem，根据高程图dem计算了地形位置指数tpi、坡度slope、坡向aspect 3个指标，然后画出垂向和时间平均土壤含水量Etz(x,y)与4个地形指标(dem、tpi、slope、aspect)的相关性矩阵图(图6)。相关性图对角线为5个变量的自分布，左下部分为两个不同变量的互分布，右上为两个不同变量的相关系数。可以看出，土壤含水量与地形位置指数tpi、坡度slope呈现弱负相关关系，与地形高程dem呈现较强负相关关系，为-0.25，与坡向呈现弱负相关。从图1和图5的对比中也可以直观看出，试验站中部地区地势较低，入渗时可能发生水流汇集现象，造成深层土壤的含水量较高。另外，由于土壤质地存在较为显著的空间变异，加上地形和作物分布因素，导致土壤水可能存在复杂的三维流动，因此地形因子和土壤墒情的线性相关性不高。

图5 不同深度z时间平均土壤含水量Et(x)等值线图Fig.5 The contour maps of the temporal mean soil moisture values at different depths

3.2.2 垂向土壤墒情

图7显示了2017年试验站水平方向及时间平均土壤含水量均值Exyt(z)及其变异性随深度z的变化规律。其中，黑色点线为均值Exyt(z)，红色阴影为均值±标准差，图7(a)～(c)的阴影面积分别代表总变异[±dxyt(z)]、水平变异[±dxy(z)]和时间变异[±dt(z)]。地下10、20、30、40、60、80 cm的平均含水量为16.7%、 19.9%、 22.5%、 25.3%、 32.6%、35.8%，由浅及深平均含水量近似呈现线性变化。因试验地地下水埋深极深(大于100 m)，不影响土壤水剖面分布，因而该分布主要受土壤质地影响。该地土壤黏粒含量及土壤容重随深度增加，因此土壤保水性也随深度增加，造成土壤含水量随深度增加。6个深度的总标准差dxyt(z)(综合时间和水平空间变异)分别为4.2%、5.0%、6.2%、6.9%、8.1%及12.0%，也呈现线性增加趋势。分开来看，水平方向造成的变异性较大，水平变异标准差dxy(z)范围为2.2%～9.0%，呈现垂向递增；时间变异标准差dt(z)范围为2.4%～2.7%，在垂向上变异性无明显变化(浅层略大)。水平变异大约解释了总变异的80%(按方差计算)。注意，本文中时间变异较小与时间取样频率(7～10 d)有关。因排水较快及雨后泥泞测量困难等客观原因，TRIM观测数据难以抓住暴雨后土壤墒情迅速上升的峰值，因此造成了时间变异偏低(尤其是表层)。安装原位实时的土壤墒情传感器可以弥补这一缺陷，但从农业水分管理角度来看，7～10 d的观测频率基本满足该地甘蔗地灌排管理需求。

3.3 土壤水时间变化规律

根据前人的研究，土壤水是影响作物生长的重要因素之一，因此对土壤水分动态监测及分析是农业生产的关键。图8展示了不同深度下，所有小区平均含水量值Exy(z,t)(红色线)及其变异性[均值加减正负标准差dxy(z,t)]。如图所示，10 cm含水量由于受气象影响较大，波动最剧烈，随着深度增大含水量值逐渐增大，但其时间变化逐渐减弱，这与研究区土壤0～40 cm保水性差而40～80 cm透水性差的土壤性质有关。可以明显看到，在10月份0～60 cm深度个别时段有明显的含水率偏低现象，而此时正好是甘蔗伸长期，根系吸需求旺盛，因此该时段应该加强灌溉。土壤墒情的时间动态和该地气象因子(降雨、参考作物腾发量)有直接联系。虽然土壤墒情时间观测间距较大，我们可以通过土壤水模拟等方法，从高密度观测的气象条件获取实时的土壤墒情动态变化规律。

图6 垂向和时间平均土壤含水量Etz(x,y)与地形指标dem、tpi、slope及aspect的相关性矩阵图Fig.6 The correlation matrix map for the vertical-and temporal-averaged soil moisture Etz(x,y) and the terrain indexes dem, tpi, slope, and aspect

图7 试验站水平方向及时间平均土壤含水量均值Exyt(z)及其变异性随深度变化Fig.7 The horizontal- and temporal- averaged soil moisture values and their variabilities versus depth

图8 不同深度水平空间平均土壤含水量Exy(z,t)随时间变化规律Fig.8 The temporal variation of the horizontally-averaged soil moisture at different observation depths

3.4 土壤墒情时间稳定性分析

对试验地所有时空含水量进行平均，可以得到该地所有地点甘蔗全生育期平均土壤墒情值为Ext= 25.45%。为了探究不同水平地点土壤含水量的代表性问题，我们将不同水平地点的土壤含水量进行深度和时间上的平均[即Ezt(x,y)]，并将Ezt(x,y)与时空平均含水量Ext的差值从小到大排序于图9。如图所示，阴影范围为均值±其标准差，红色线为0，交叉点即为最佳点，表明该小区(3-2号)观测的时间和深度平均土壤含水量Ezt(x,y)与Ext=25.45%十分接近。不同小区[即不同(x,y)坐标]可能低估(达到-7%)或者高估(+10%)试验地总体土壤墒情。通过时间稳定性分析优选的小区3-2的土壤含水量Ez(x*,y*,t)和试验区总空间平均土壤墒情Ex(t)有较好的相关性(图10)，能反映其时间动态变化。采用线性拟合公式，可以得到R2=0.649，平均绝对观测误差为1.23%，平均平方误差L2指标为2.24。通过首年大量进行空间观测，并进行时间稳定性分析，并在代表性点安装原位土壤墒情传感器，可以有效获取该地平均土壤墒情，大量节约后续观测成本[14]。相比之下，如果任意选择观测点，并不加以校核修正，可能会严重高估区域墒情(例如15-2号小区)，延误灌溉决策，造成甘蔗减产。

图9 不同小区深度及时间平均土壤含水量Ezt(x,y)与时空总平均含水量Ext差值排序图Fig.9 The ranking of plots with respect to the temporal-and depth-averaged soil moisture minus the total spatiotemporal mean soil moisture

4 讨论

本文基于广西崇左2017年甘蔗试验田TRIM观测的大量土壤水数据，分析了广西典型山丘坡地土壤墒情的时空变异规律，探究了其时空变化的影响因素，并采用时间稳定性分析得到了最能代表该地区总平均土壤墒情的观测位置。不同时间的空间平均含水率Ex(t)在21%到30%之间波动，不同位置的时间平均含水量Et(x)在10%到60%之间波动，从变异系数看均呈现弱变异，但时间平均含水量标准差dt(x)大于空间平均含水量标准差dx(t)，即空间变异更加显著。单独分析空间变异，得到该地土壤墒情的水平相关长度为4～12 m；水平变异和该地起伏地形有一定关系，中部地势低洼，可能会存在壤中流汇水现象，导致含水量增大，但由于地形、土壤质地和土壤水动力学运动存在复杂的关系，土壤墒情和地形指标的线性关系不够显著。从时间变异性来看，土壤墒情的时间变化与气象条件显著相关，因此采用土壤水模型应该可以较好地刻画其时间变异；而空间变异主要由地形和土壤质地变异造成，目前由于计算成本限制，构建三维非均质土壤水模型有较大困难。基于土壤墒情的时间稳定性分析，我们探究了不同观测点对试验区平均含水率预测的影响，发现利用时间稳定性优选代表点的土壤含水量与区域平均值的相关性和无偏性均较好。这说明利用时间稳定性分析可以有效地节约山丘坡地的土壤墒情观测成本。