三相LCL型逆变器双闭环电流控制策略研究
2020-07-14陈蓓任鹤党胜梅伏亮亮
陈蓓 任鹤 党胜梅 伏亮亮

摘 要: 在比例复数积分控制器基础上增加截止频率[ωc],并联一个积分控制器,构成混合控制器,以此设计一个能抑制谐波,实现零稳态误差跟踪的逆变控制策略。与比例复数积分控制器相比,该混合控制器不仅可以完全消除稳态误差,而且使系统具有更好的快速性。在三相静止坐标系上实现复数域的实数化,通过Simulink仿真模型对理论分析进行仿真验证,在三相LCL型逆变器实验平台进行实验验证。仿真与实验结果证明,采用该混合控制器的控制策略具有良好的控制效果。
关键词: 逆变器; 双闭环; 电流控制; LCL逆变器; 模型分析; 仿真实验
中图分类号: TN721?34 文獻标识码: A 文章编号: 1004?373X(2020)10?0014?04
Research on double closed?loop current control strategy for three?phase LCL inverter
CHEN Bei1, REN He2, DANG Shengmei3, FU Liangliang4
(1. School of Electrical and Control Engineering, Shaanxi University of Science & Technology, Xian 710021, China;
2. The 39th Research Institute of China Electronics Technology Group Corporation, Xian 710065, China;
3. Weihai Yihe Specialty Equipment Manufacturing Co., Ltd., Weihai 264200, China;
4. State Grid Lanzhou Electric Power Supply Company, Lanzhou 730070, China)
Abstract: The cut?off frequency [ωc] is added on the basis of the proportional complex integral controller, and an integral controller is connected in parallel to form a hybrid controller. An inverter control strategy is designed to suppress harmonics and realize zero steady state error tracking. In comparison with the proportional complex integral controller, the hybrid controller can not only eliminate the steady?state error completely, but also make the system have better rapidity. The real number of the complex domain is realized in the static three?phase coordinate system. The theoretical analysis is verified by the Simulink simulation model, and the experimental verification is performed on the experimental platform of the three?phase LCL inverter. Both simulation and experiment results prove that the control strategy of this hybrid controller has a certain control effect.
Keywords: inverter; double closed loop; current control; LCL inverter; model analysis; simulation experiment
0 引 言
逆变器广泛应用于太阳能发电、风能发电以及工业现场等多种领域,科技的发展又使得各种设备对逆变器控制的要求越来越高。传统逆变控制方法有双闭环PI控制[1]、无差拍控制[2]、比例谐振控制[3]、滑模控制[4]等。其中PI控制器虽然算法简单、可靠性高,但传统的PI控制方法对正弦的交流量无法实时跟踪,导致相位滞后,从而达不到理想的控制效果[5]。传统无差拍控制存在延时和依赖精确的电气模型参数等不足。比例谐振控制的参数较难整定,且对谐波的补偿作用有限。滑模控制实质上是一种非线性控制方法,其控制特性使得其存在抖振等问题。近些年,有学者提出比例复数积分控制器[6]。该控制器虽然能够完美地实现对基波的无静差跟踪,且抑制了谐波,但在数字化实现过程中容易导致频率偏移,对基波的跟踪效果变得较差。
本文通过在比例复数积分控制器基础上增加了截止频率[ωc],以及并联积分控制器,构成一个混合控制器,设计了一个便于工程应用,具有谐波抑制,能实现零稳态误差的三相LCL型逆变器双闭环电流控制策略。采用该混合控制器的双闭环电流控制策略可以消除稳态误差,使系统具有更好的快速性,同时降低输出电压波形的谐波畸变率,从而提高输出电能质量。
1 系统模型分析
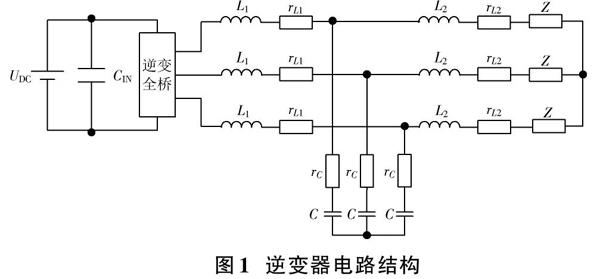
逆变器是由逆变桥、直流电源和滤波电路等组成的电力电子装置或设备,可以把直流电转变成任意形式的交流电,并调整所需要的频率、电压或电流的值。带LCL滤波器的逆变器电路结构如图1所示。
由图1可看出,逆变器的电路结构主要包含直流稳压电源[UDC]、母线电容[CIN]、三相逆变全桥、三相LCL滤波器以及三相负载。LCL滤波器由逆变测电感[L1],滤波电容[C],负载侧电感[L2]组成,其中[rL1]为电感[L1]的等效电阻,[rL2]为电感[L2]的等效电阻,[rC]为滤波电容[C]的等效电阻。
若设[uk]为逆变全桥输出电压,[uo]为负载侧电压;令逆变侧电感[L1]流过的电流[iL1k]、负载侧电感[L2]流过的电流[iL2k]、滤波电容[C]两端的电压[uCk]為状态变量[7],则可得状态空间方程[8]为:
[i′L1k=ukL1-1L1uCki′L2k=1L2uCk-uoL2u′Ck=1CiL1k-1CiL2k] (1)
2 电感电流反馈的控制策略分析
2.1 控制策略
本文考虑采用电感电流反馈的双闭环控制策略[9],将逆变全桥的工作过程看作一个比例环节[KPWM],若以SVPWM方式控制开关器件开通与关断为例,[KPWM]取值为直流母线电压的[12]。设[Gu(s),Gi(s)]分别为电压环和电流环的传递函数,控制框图如图2所示。
将控制框图化简可以得到逆变系统内环电流环的传递函数:
[G内(s)=(L2Cs2+1)KK1Cs3+KL2Cs2+(L1+L2)s+K] (2)
式中:[K=Gi(s)KPWM];[K1=L1L2]。
同时可得到逆变器系统输出电流[iL2k]的闭环传递函数:
[iL2k=Gr(s)iref-Guo(s)uo] (3)
式中:
[Gr(s)=KGu(s)K1Cs3+L2CKs2+L1s+1+(1+K)Gu(s)] (4)
[Guo(s)=b2s2+b1s+b0a3s3+a2s2+a1s+a0] (5)
式(4)中[K]和[K1]与式(2)相同,式(5)中:
[b2=K2PWMG2i(s)CL1+L21]
[b1=K3PWMG3i(s)C+2KPWMGi(s)L1]
[b0=K3PWMG3i(s)]
[a3=K2PWMG2i(s)CL1L2+L21L2]
[a2=K3PWMG3i(s)CL2+2KPWMGi(s)L1L2]
[a1=K3PWMG3i(s)L2+K2PWMG2i(s)L1]
[a0=K3PWMG3i(s)(1+Gu(s))]
[Gr(s)]可以看作系统跟踪输入参考电流iref的传递函数,使得系统能够无静差跟踪输入;[Guo(s)]可以看作系统抑制输出电压干扰的传递函数,从而使得系统具有一定的抗扰性能。
2.2 控制器
传统的PI控制器通常适用于直流控制系统,可实现直流分量的零稳态误差控制,而逆变器控制为交流控制。当PI控制器应用于交流控制时,会存在一个无法消除的稳态误差。
因此选择采用比例复数积分控制器(PCI)[9],其传递函数为:
[Gu(s)=kP+kIs-jω0] (6)
为了避免在数字芯片上实现控制算法时导致频率偏移,通常需要在控制器的分母上加一个截止频率[ωc],构成准比例复数积分控制器:
[Gu(s)=kP+kIs-jω0+ωc] (7)
将式(7)代入式(4)中进行分析可知,式(7)无法实现当[s→jω0]时,有[Gu(s)→1],因此,本文采用准比例复数积分控制器并联积分控制器的混合控制器。其传递函数表示为:
[Gu(s)=kP+kI1s-jω0+ωc+kI2s] (8)
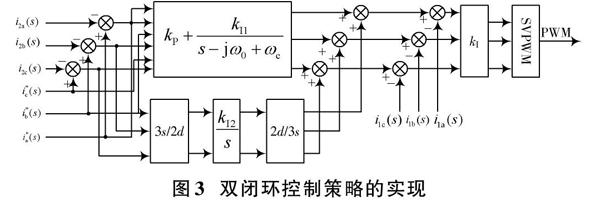
将式中的积分控制器等效到静止坐标系可得到谐振控制器[3],因此不难得出,式(8)可以实现当[s→jω0]时,有[Gu(s)→1]。双闭环电流反馈的混合控制策略实现方法如图3所示。图中:[i2a(s)],[i2b(s)],[i2c(s)]为采样得到的L2的三相电流信号;[i*a(s)],[i*b(s)],[i*c(s)]为参考电流信号;[i1a(s)],[i1b(s)],[i1c(s)]为采样得到的L1的三相电流信号。
2.3 控制器的离散化
根据复变函数理论可知,虚数单位j代表其幅值不变,而相位往正方向[9]旋转90°。那么在三相系统中,可以利用三相静止坐标系实现j,以a相为例得到如图4所示的PCI控制原理图。
图中[c(s)]和[r(s)]的关系可表示为:
[c(s)=kI1s+ωc·r(s)] (9)
可得到[c(t)]的差分方程为:
[c(k)=2-Tωc2+Tωc·c(k-1)+TkI12+Tωc·[r(k)+r(k-1)]] (10)
式中,[r(k)]可表示为:
[r(k)=xa(k)-ω03kI·[zb(k)-zc(k)]] (11)
则准比例复数积分控制器在三相静止坐标系上的控制器离散化可表示为:
[ya1(k)=kPxa(k)+c(k)] (12)
若设积分控制器的输入在时域上为xh(t),输出在时域上为[yh(k)],则积分控制器的差分方程可表示为:
[yh(k)=yh(k-1)+TkI22·[xh(k)+xh(k-1)]] (13)
3 仿真与实验验证
3.1 仿真验证
为了验证采用混合控制器的双闭环电流控制策略的有效性,通过搭建Simulink仿真模型进行研究。
根据文献[10]论证的LCL滤波器参数设计方法,搭建一台3.3 kW的并网逆变器,其输出频率为50 Hz,母线电压为500 V,系统开关频率为20 kHz,滤波电感L1为3.5 mH,L2为1 mH,滤波电容C为17 μF。本文取[ωc]的值为5,根据凑试法可得kI =0.22,若只考虑采用控制器比例环节kP,即kI1,kI2均为0,本文选取系统带宽[fb=700] Hz,可求比例系数kP的值为10.3,复数积分参数kI1的值为36.3,积分参数kI2的值[9]为398.8。
该新型逆变策略下的逆变器输出电流波形如图5所示。从图中可以看出,系统启动后约一个周期内,负载侧电感L2输出电流迅速追踪参考电流,并与之达到同频同幅。
图6为采用比例复数积分控制器的电流双闭环控制策略时,负载侧电感L2输出电流波形,与图5相比可以看出,采用混合控制器的双闭环电流控制策略比采用比例复数积分控制器的电流双闭环控制策略具有更好的快速性。
在采用混合控制器的双闭环电流控制策略的逆变系统稳定运行状态下,对负载侧电感L2输出的电流波形进行谐波分析,如图7所示。电流谐波畸变率为0.54%。再对采用比例复数积分控制器的电流双闭环控制策略的逆变系统稳定运行状态下,对负载侧电感L2输出的电流波形进行谐波分析,其总谐波畸变率保持在0.54%左右。从此可以看出,该混合控制器对谐波的抑制作用可以达到比例复数积分控制器相同的水平。
系统电流误差结果如图8所示,在0.06 s时突增1倍的负载。从图中可以看出,系统启动后在一个周期内迅速进入稳定运行状态,突增1倍负载后,误差电流震荡6个周期后系统再次进入稳定运行状态。
3.2 实验验证
为了进一步验证理论分析和仿真验证的正确性,采用TI公司32位定点DSPTMS320F2812 芯片,搭建一个逆变器实验平台。图9为系统在a时刻突增负载前后的输出电流波形,对比图8的仿真波形可以看出二者一致,均为突增負载后约6个周期内,系统再次达到稳定状态,从而验证了系统具有较强的抗干扰能力。
4 结 语
本文将比例复数积分控制基本理论应用于三相逆变器,并在此基础上增加截止频率[ωc],同时并联一个积分环节,从而构成一个混合控制器,逆变器电流双闭环控制系统外环使用该控制器,内环使用比例控制器,通过搭建的Simulink仿真模型与PCI控制器的控制效果进行对比仿真研究,在三相逆变器实验平台上进行了实验验证。通过仿真和实验可以看出,该控制策略虽然结构变得复杂,但具有更好的稳态性能、动态性能,以及极强的抗干扰能力,且更具有实际应用价值。
参考文献
[1] 吴健芳,王飞,赵佳伟.基于PI+重复控制的单相逆变器研究[J].通信电源技术,2016,33(4):9?11.
[2] 赵明,李欢,王省伟,等.基于无差拍电流控制的光伏并网逆变器研究[J].煤矿现代化,2017(1):63?65.
[3] 雷亚雄,李建文,李永刚.基于准PR调节器电流双闭环LCL三相并网逆变器控制[J].电力系统保护与控制,2014,42(12):44?50.
[4] 陈智勇,罗安,陈燕东,等.逆变器并联的自适应滑模全局鲁棒电压控制方法[J].中国电机工程学报,2015,35(13):3272?3282.
[5] PAN D, RUAN X B, BAO C L, et al. Capacitor?current?feedback active damping with reduced computation delay for improving robustness of LCL?type grid?connected inverter [J]. IEEE transactions on power electronics, 2014, 29(7): 3414?3427.
[6] 曹靖,童朝南,周京华,等.一种并网逆变器的新型复合控制设计[J].仪器仪表学报,2017,38(5):1296?1303.
[7] 雒向东,崔剑波.光伏并网逆变器LCL滤波器参数优化设计[J].沈阳工业大学学报,2016,38(6):601?605.
[8] 郭小强.光伏并网逆变器通用比例复数积分控制策略[J].中国电机工程学报,2015,35(13):3393?3399.
[9] 王一丁,缪志农.双环准比例谐振控制逆变器的分析与仿真[J].攀枝花学院学报,2016,33(z1):118?122.
[10] 刘述喜,陈宝刚,杨儒龙.基于LCL滤波的单相虚拟矢量并网逆变器[J].重庆理工大学学报(自然科学),2017,31(9):132?137.
