基于多传感器的数据融合算法研究
2020-07-14敬如雪高玉琢
敬如雪 高玉琢


摘 要: 文中提出基于多传感器的数据融合算法,该融合方法先对数据进行一致性检验,剔除传感器测量的异常数据,得到最优数据集;其次以支持度与自适应加权估计理论为基础,提高融合数据的精确度,该算法不需要提前知道任何先验条件。实际应用结果验证了算法的准确性,并进行了Matlab仿真。仿真结果表明,此方法计算简便,可以获得比有限个传感器的算术平均值与传统的自适应加权算法融合值更精确的估计结果,具有较高的可靠性和抗干扰性,可用于测量结果具有正态分布特性的多传感器测量系统。
关键词: 多传感器; 数据融合; 数据一致性; 支持度; 自适应加权算法; 仿真分析
中图分类号: TN919?34 文献标识码: A 文章编号: 1004?373X(2020)10?0010?04
Research on data fusion algorithm based on multi?sensor
JING Ruxue, GAO Yuzhuo
(School of Information Engineering, Ningxia University, Yinchuan 750000)
Abstract: The data fusion algorithm based on multi?sensor is proposed in this paper. In this fusion method, the consistency of the data is firstly checked, and the abnormal data measured by the sensor is eliminated to obtain the optimal data set. The accuracy of the fusion data is improved based on the support degree and self?adaptive weighted estimation theory. The application of the algorithm does not need to know any prior conditions in advance. The practical application results verify the accuracy of the method, by which the Matlab simulation is carried out. The simulation results show that the method is simple to calculate and can obtain more accurate estimation results than that of the fusion value of the arithmetic mean value of a finite number of sensors with the traditional self?adaptive weighting algorithm. It has the higher reliability and anti?interference and can be used in multi?sensor measurement systems with normal distribution characteristics.
Keywords: multi?sensor; data fusion; data consistency; support degree; self?adaptive weighting calculation; simulation analysis
0 引 言
物联网作为自动化和智能化的融合体,它的核心是“互联网+传感网”, 传感器具有低能耗、低成本、高精度和集成化的特点[1?3],各类传感器是传感网中的必备节点。但由于传感器本身精度和工艺灵敏度、传输误差、高斯噪声以及周围环境对测量数据的干扰影响,在实际情况下的数据测量中,传感器所处的位置不同,对物体同一属性参数的测量数据有不同程度的偏差。为减少测量偏差,提高数据精度,一方面,需要提升传感器硬件本身的测量精度;另一方面,利用算法优化,对测量的原始数据集进行去噪处理,可得到较高的数据融合结果,且抗干扰能力较强。陈彦如等人研究设计CMOS温度传感器[4]的工作温度范围是-125~-45 ℃,其测量精度误差绝对值不超过1.5 ℃。本文在文献[5]的基础上,研究一种新的参数估计方法,此方法以自适应加权估计理论为基础,对多传感器采集到的原始数据进行一致性检验,找到数据最优融合集;其次通过关系矩阵,找到支持度最高的传感器,以其测量数据代替异常数据,进行自适应加权数据融合来估计出一个最优参数。该算法不仅计算过程简单,而且可以充分利用实验中所有的测量数据,并用Matlab进行了实例仿真。
1 数据一致性检验
对多传感器测量的原始数据进行融合之前,利用数据探测技术中的分布图法[6]找到并剔除异常数据[7]。分布图中反映数据分布结构的主要参数有:中位数TM、上分位数FU、下分位数FL和分位数离散度dF。设对物体的某一性能指标的检测采用N个传感器彼此独立地进行参数测量,按照测量参数从小到大的顺序进行排列,得到一组检测序列:T1,T2,…,Tn-1,Tn。其中T1是检测序列的下限,Tn是检测序列的上限。定义中位数TM为:
[TM=Tn2+Tn2+12] (1)
上五分位数FU为区间[TM,Tn]的中位数,下五分位数FL为[T1,TM]的中位数。分位数离散度为:
[dF=FU-FL] (2)
设定与中位数的距离大于[α?dF]的数据为异常数据,即无效数据的判断区间为:
[Ti-TM>α?dF] (3)
式中:[α]为常数,一般取值为0.5,1.0,2.0等;[i]的取值为1,2,3,…,n-1,n。当检测序列的异常数据被找到且被剔除之后,剩下的数据构成最优数据集。
2 相关支持度
在数据融合集中,数据Xi和Xj分别是第i个传感器和第j个传感器的检测数据,且服从高斯分布,以其概率分布曲线Pi(x)和Pj(x)作为各传感器的特性函数[8],xi,xj记作Xi,Xj的一次观测值,σi,σj为其方差,引进置信距离测度,便于直观反映xi与xj之间的偏差。
[dij=2xixjpi(xxi)dx] (4)
[dji=2xjxipj(xxj)dx] (5)
式中:dij为第i个传感器与第j个传感器所测数据之间的置信距离测度。
[pi(xxi)=12πσiexp-12x-xiσi2] (6)
[pj(xxj)=12πσjexp-12x-xjσj2] (7)
假设最优数据集有M个数据,则由置信距离测度dij(i,j=1,2,…,m)构成置信矩阵Dm:
[Dm=d11d12…d1md21d22…d2m????dm1dm2…dmm] (8)
给出融合上限θij,令关系系数rij的取值为:
[rij=1, dij≤θij0, dij>θij] (9)
当rij=1,表示第i个传感器支持第j个传感器,反之,rij=0,则第i个传感器不支持第j个传感器;当rij=1且rji=1,则表明第i个传感器与第j个传感器相互支持。N个具有相同精度的传感器,在测量数据进行数据融合后,可将参数精度提高到一个传感器N1/2倍。通过关系矩阵Rm可找到支持度最高的传感器,其测量的数据称为超数据,用超数据代替被剔除的异常数据,最后进行动态加权融合估计。关系矩阵Rm如下:
[Rm=r11r12…r1mr21r22…r2m????rm1rm2…rmm] (10)
即关系矩阵Rm的第i列之和为第i个传感器被其他传感器支持的支持度。传感器支持度的计算公式为:
[si=j=1mrji, i=1,2,…,m] (11)
3 自适应加权融合估计算法
自适应加权融合估计算法的思想:基于总均方误差最小的前提下,依据每个传感器实时测量到的数据,动态为各传感器分配所对应的最优加权因子Wi(i=1,2,…,n),其中传感器的方差越大,对应所分配的权值越小,以求得最终的估计值[X]贴近真实值X。假设:采用n个传感器测量某事物的同一特性参数,σ1,σ2,…,σn是n个传感器的方差,测量的理论值为X,每个传感器的检测数据为Xi(i=1,2,…,n),各检测数据彼此相互独立且是X的无偏估计,估计后的参数就是最终所求的融合结果。其中[X]和Wi必须满足:
[X=i=1nWiXi] (12)
由式(12)、式(13)推导出总均方误差[σ2]:
[i=1nWi=1] (13)
[σ2=Ei=1nW2i(X-Xi)2=i=1nW2iσ2i] (14)
根据多元函数求极值理论,求得在总均方误差σ2最小的条件,各传感器所对应的权值为Wi(i=1,2,…,n),当方差越小时,其对应的权值越大。最小总均方误差[σ2min]为:
[σ2min=1i=1n1σ2i] (15)
其对应的每个传感器的加权因子[Wi]为:
[Wi=1σ2ik=1n1σ2k, i=1,2,…,n] (16)
通过式(16)对多个传感器相应权值Wi的计算,代入式(12),进而可得到最终融合结果[X]。
4 算法举例
基于文献[9]中的数据,采用10个同种传感器测量物体的同一特性参数,指标参数的实际值为1.000,测量到的原始数据如表1所示。
序号i 观测值xi 方差[σ2i] 1 1.000 0.05 6 0.650 0.25 2 0.990 0.07 7 1.010 0.10 3 0.980 0.10 8 1.020 0.10 4 0.970 0.20 9 1.030 0.20 5 0.500 0.30 10 1.500 0.30 ]
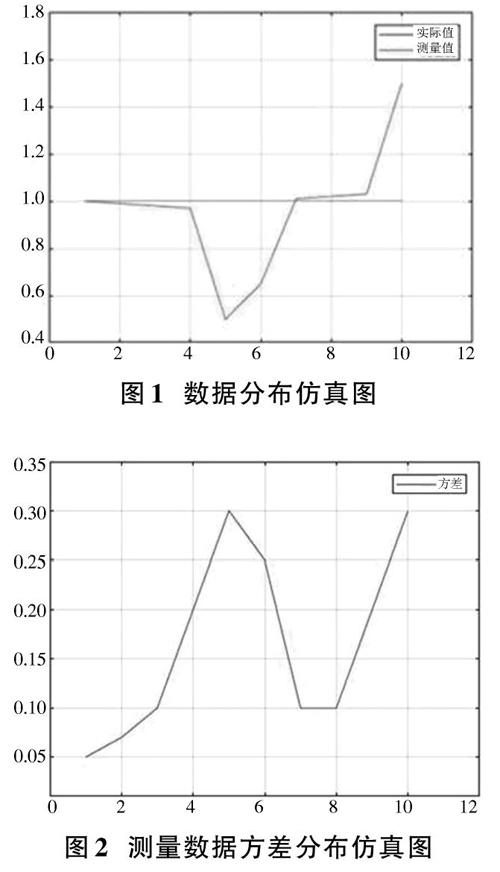
实际值与测量值的分布特征仿真图如图1所示,测量值对应的方差分布仿真图如图2所示。
对10个传感器同一时刻所采集到的样本数据进行数据一致性检验。先对原始数据按从小到大顺序排序得到:0.500,0.650,0.970,0.980,0.990,1.000,1.010,1.020,1.030,1.500。利用式(1)求得中位数:TM=(0.990+1.000[)2]=0.995,由式(2)知,分位数的离散度dF=1.005-0.965=0.04,此次[α]取2.0,无效数据的判断区间为[Ti-0.995]>0.08,距离大于0.08的数据为异常数据,距离越大,则表明此传感器的数据采集准确率越低;反之,传感器的数据测量准确率越高。经过计算,5号、6号及10号传感器的数据与中位数的偏差分别为0.495,0.395及0.505,均远大于0.08,视为异常数据进行剔除,剩下的参数组成最优数据集{x1,x2,x3,x4,x7,x8,x9},假設有一变量Yi服从高斯分布,令y1=x1,y2=x2,y3=x3,y4=x4,y5=x7,y6=x8,y7=x9,数据集变成{y1,y2,y3,y4,y5,y6,y7},且使融合上限θij=0.07,则置信矩阵D7和关系矩阵R7如下:
[D7=00.040.070.110.040.070.110.0300.030.060.060.090.120.050.0300.030.080.100.130.050.040.0200.070.090.110.030.050.080.1000.030.050.050.080.100.130.0300.030.050.070.090.110.040.020] [R7=1100100111110011110001111000110011110001111000111]
观察矩阵[R7]得,1号传感器的支持度为7,为支持度最高的传感器,2号和7号传感器的支持度同为5,支持度较次之,3,4,8,9号传感器支持度都是3,最次之。因此用1号传感器的超数据代替5号、6号及10号传感器的测量值,经过处理后的数据参数表如表2所示,依据式(16),求得预处理后各传感器的加权因子见表3。
数据预处理后得到的方差用Matlab仿真得到图3。
利用式(12)可计算融合参数:
[X=]1.000[×]0.148 9+0.990[×]0.106 4+0.980[×]0.074 5+0.970[×]0.037 2+1.000[×]0.148 9+1.000[×]0.148 9+1.010[×]0.074 5+1.020[×]0.074 5+1.030[×]0.037 2+1.000[×]0.148 9
=0.999 581
对于10个测量原始数据采用简单的算术平均法:
[X=] (1.000+0.990+0.980+0.970+0.500+0.650+1.010+1.020+1.030+1.500[)10]=0.965
利用算术平均值法的计算结果是0.965,传统的自适应加权方法计算出数据融合结果是0.983 0,改进后的自适应加权算法结果是0.999 581。经过数据融合对比发现,采用本文提出的数据融合算法估计的参数精度明显提高,具有较高的可靠性和鲁棒性。
5 结 语
本文提出的融合算法不需要知道任何先验概率,且可充分使用到任何一个传感器测量到的数据,利用数据的冗余性和互补性进行数据融合,根据计算结果的对比,参数估计准确率提高。在使用多个传感器对事物同一属性进行参数测量时,针对测量到的个别异常数据,提出基于数据一致性与支持度的自适应加权估计算法。首先,利用数据一致性对原始数据进行预处理,剔除异常数据,寻找最优数据集;其次,通过支持度选出测量最准确数据的传感器,用超数据代替异常数据进行下一步的融合估计;最后,在均方差误差最小的情况下,应用自适应加权算法进行最终的参数估计。自适应加权数据融合算法不仅可以广泛应用到多传感器的温室系统,而且对变速箱故障诊断与风电轴承故障诊断[10?11]及磨矿粒度建模[12]等都有较好的改进效果。
注:本文通讯作者为高玉琢。
参考文献
[1] 方加娟,鹿艳晶,安鹏.传感器网络中的节点能耗监测软件设计与实现[J].现代电子技术,2017,40(12):53?55.
[2] 黄志武,王曙霞.基于S3C2410的高精度传感器节点嵌入式设计[J].现代电子技术,2017,40(19):33?36.
[3] 张严.基于MEMS海洋湍流传感器实验研究[J].现代电子技术,2016,39(1):137?139.
[4] 陈彦如,陈志铭.一种大量程低误差CMOS温度传感器[J].微电子学,2016,46(5):605?607.
[5] 孙田川,刘洁瑜.基于支持度和自适应加权的MEMS陀螺信息融合算法[J].传感技术学报,2016,29(10):1548?1552.
[6] 张兰勇,陆晴,耿文杰,等.基于贴近度及分布图法的数据深度融合算法研究[J].兵器装备工程学报,2016,37(11):49?55.
[7] 郑宝周,吴莉莉,李富强,等.基于异常数据预处理和自适应估计的WSN数据融合算法[J].计算机应用研究,2019(9):1?8.
[8] CHEN J, HUANG N, XIONG G, et al. Adaptive weighted mean filtering algorithm based on confidence interval [J]. Journal of Nanjing University of Science & Technology, 2017, 41(3): 307?312.
[9] 万树平.基于最小一乘估计的多传感器信息融合方法[J].计算机工程,2010,36(2):257?259.
[10] JING Luyang, WANG Taiyong, ZHAO Ming, et al. An adaptive multi?sensor data fusion method based on deep convolutional neural networks for fault diagnosis of planetary gearbox [J]. Sensors, 2017, 17(2): 414.
[11] 李红,孙冬梅,沈玉成.改进加权融合算法与双谱技术在风电轴承故障诊断中的应用[J].电子器件,2018,41(4):898?904.
[12] 李德鹏,代伟,赵大勇,等.一种基于鲁棒随机向量函数链接网络的磨矿粒度集成建模方法[J].工程科学学报,2019,41(1):67?77.
