基于Holt-Winters模型的天然气负荷预测
2020-07-14胡凯
胡 凯
(合肥燃气集团有限公司,安徽 合肥 230001)
0 引言
近年来,合肥地区随着城市规模的不断扩大,燃气民用户与工业、公建和商业用户数的持续增加,城镇天然气消费量持续增加。开展燃气负荷的预测工作是实现调度燃气管网输配的基础。燃气负荷受到季节气温、居民的饮食起居的影响较大,具有一定的波动性、周期性,给预测研究带来一定的挑战。国内外开展了城镇天然气负荷特点的研究[1],建立相应的预测模型,其中预测模型主要采用回归分析[2]、灰色理论[3]、时间序列[4-6]、人工神经网络[7]等理论,本文基于Holt-Winters理论构建预测模型对企业燃气负荷进行科学预测。
1 Holt-Winters模型的基本理论
Holt-Winter模型[8]是Holt于1957年提出的一种基于统计学的时序数据的预测模型,具有较好的预报重复性和季节性趋势数据分析的能力。该模型的基本思想是将具体线性趋势、季节性趋势和随机变动的时间序列进行分解研究,并与指数平滑法结合,分别对长期趋势、季节性趋势和随机变动做出估计,建立预测模型,外推预测值。Holt-Winter模型的方法可以处理趋势性和季节性变化,并能将随机波动的影响过滤掉。因此,其特别适用于包含趋势和季节性变化的时间序列的预测问题。常用的Holt-Winter季节模型主要包括加法模型和乘法模型。
1.1 Holt-Winter加法模型
加法模型的初始值计算公式
(1)
加法模型的基本公式
(2)
1.2 Holt-Winter乘法模型
乘法模型的初始值计算公式
(3)
乘法模型的基本公式
(4)
式(1)~(4)中,Xt为t时刻的观测值;St为t时刻的稳定成分;It为t时刻的季节成分;bt为t时刻的趋势成分;Ft+m为m时刻的预测值;m为预测的期数;L为季节长度;α、β、γ∈[0,1]为平滑参数;α、β、γ取值原则是预测值和实测值之间的均方根误差最小。
均方根误差基本公式:
(5)
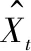
2 模型的构建与预测
2.1 数据来源
统计合肥燃气集团有限公司2015—2019年每季度于合肥市政务公开网发布的经济运行情况信息,具体数据见表1所示。
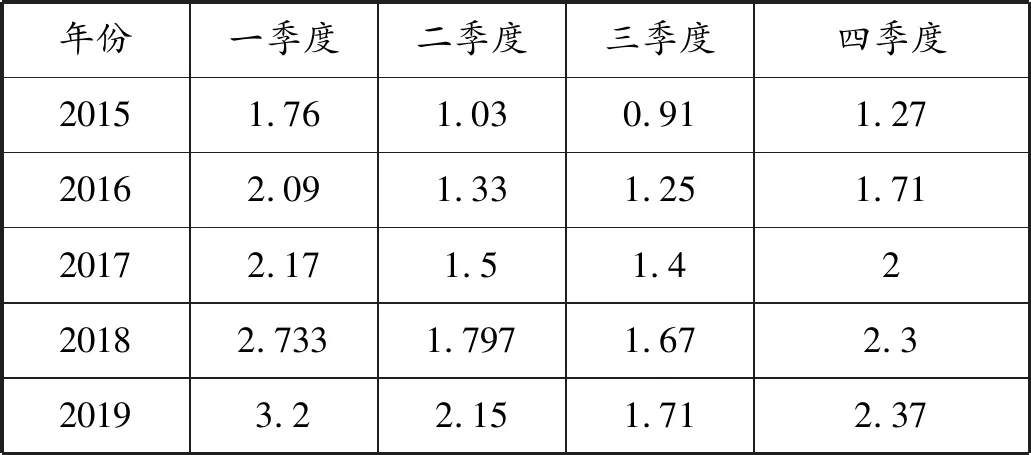
表1 2015—2019年各季度燃气负荷
通过绘制2015—2018年企业燃气负荷的折线图,观察用于建模数列的基本特征。
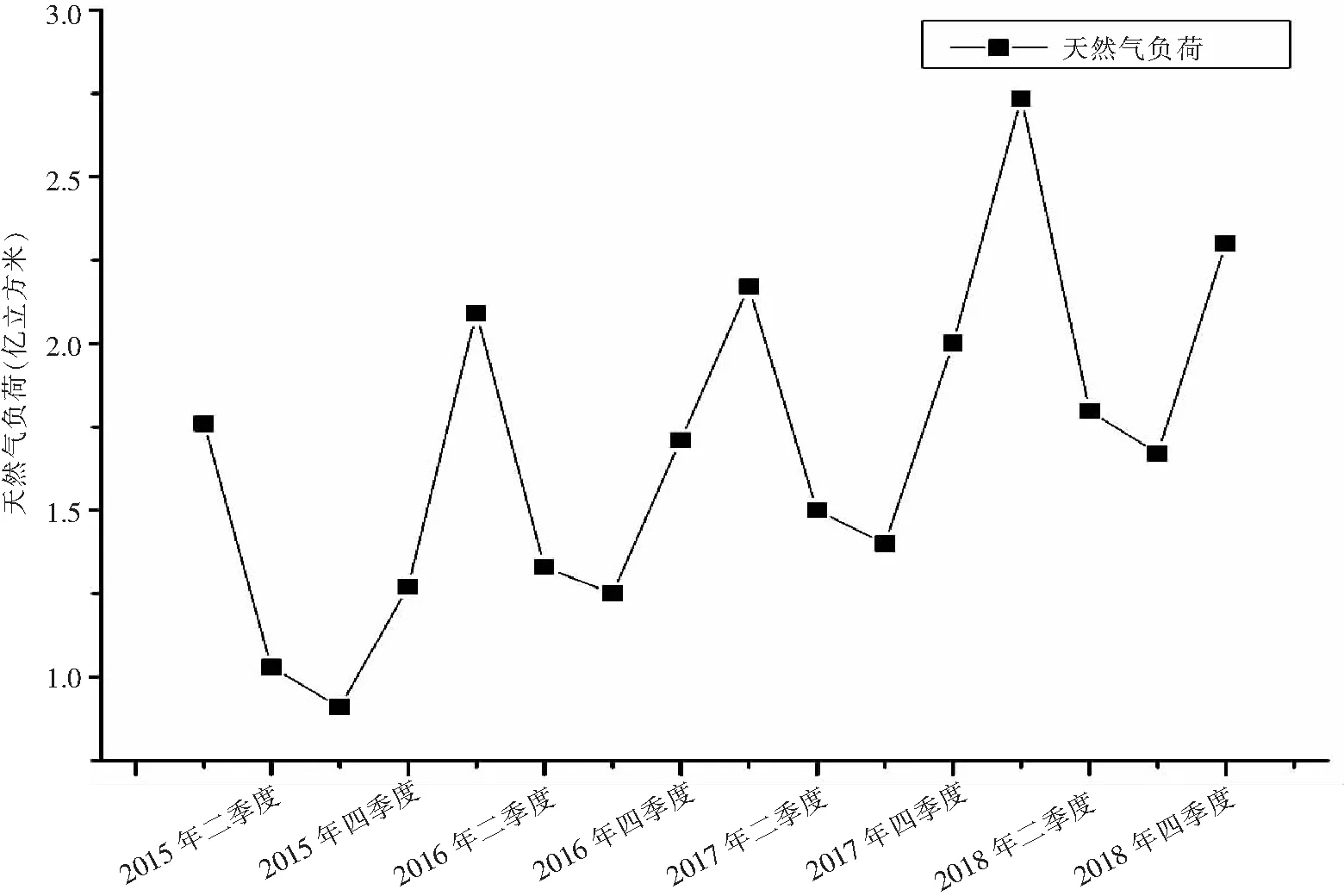
图1 燃气负荷折线图
从图1可以看出燃气负荷具有逐年增长的趋势,同时负荷随着季节变动,二季度与三季度是负荷的低谷,一季度负荷是年度供应高峰。这种情况主要因为天气温度随季节变化,春冬两季温度较低,居民燃气取暖、工业取暖等燃气用量增加。天然气负荷量随季节变化存在季节性与趋势性,符合winters模型的适用条件。
2.2 数据分析
2.2.1 模型统计量分析
应用SPSS软件,对数据进行处理,建立Holt-Winter模型,得到相应的模型统计量如表2所示。
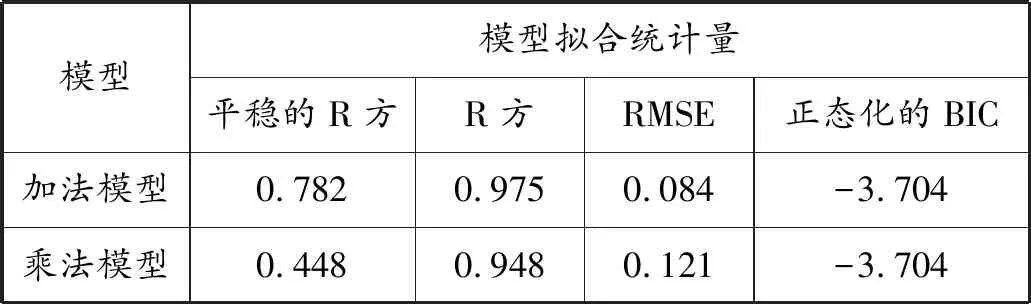
表2 模型拟合统计量
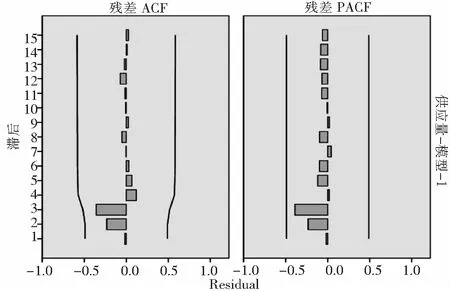
图2 加法模型的自相关与偏自相关图
从表2中可以知,平稳的R方时序列稳定后的R方,适用于原始数列为非平稳数列。R方表示该统计值用于表示所能解释的数据变异占总变异量的比例。2个统计量越大表示结果越佳。RMSE为均方误差的平方根,代表模型预测值与观测值的差异大小,数值越小表示结果越佳。BIC值表示的是模型对数据的释度,BIC值越小,该模型对数据解释力越强。从表2中对比两种模型各项统计量,可以看出Holt-Winter加法模型优于乘法模型。
2.2.2 残差序列自相关与偏自相关分析
从图2中可以知,残差ACF与残差均落在-0.95~0.95的置信区间内,说明模型残差数列为白噪声序列,Holt-Winter加法模型适合用于预测燃气负荷。
2.3 Holt-Winter模型建模与预测
利用收集的燃气负荷数据作为为目标变量进行预测分析,以2015—2018年的16组数据进行建模,以2019年4组数据来检查模型的预测效果。Holt-Winter加法模型的拟合值和观测值的关系如图3所示。

图3 观测值与模型拟合值比较图
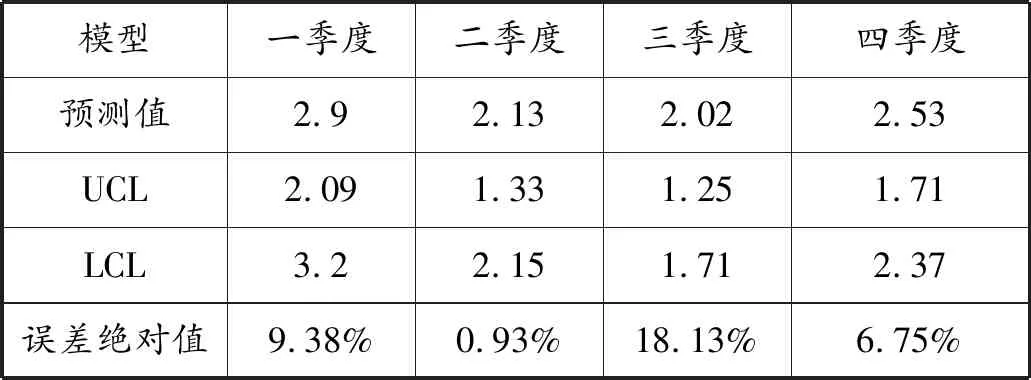
表3 2019年各季度燃气负荷预测值
从表3中可以看出,误差绝对值误差最大发生在三季度,误差为18.13%;误差绝对值最小发生在二季度,误差为0.93%。2019年前两季度平均误差为5.2%,后两季度平均误差为12.4%,四季度平均误差为8.8%。模型预测区间延长误差存在增加的现象,模型的预测结果较为可靠。
3 结论
1)燃气负荷随城市用气客户数的增长呈现一定的线性增长趋势,受气温变化影响存在季节周期性变化。Holt-Winter模型可综合数据的长期变化趋势与季节性因素,有效规避随机性影响,预测结果基本控制在10%以内,可有效预测企业短期燃气负荷。
2)Holt-Winter预测模型是从数据序列本身出发,未考虑燃气居民用户数、工商用户数等影响因素,因此预测结果存在一定的误差。在实际应用中,应当不断更新数据,完善预测模型,才能提高模型的可靠性。
