锻造液压机双缸同步控制系统研究
2020-07-14李胜永
李胜永
(南通航运职业技术学院,江苏 南通 226010)
引言
工业发展对锻造液压机的控制精度需求越来越高[1]。现在锻造液压机多采用双液压缸作为驱动机构,容易出现2个液压缸不同步,导致偏载和机械结构卡死,因此需采用合理的同步控制策略提高两缸同步精度。
为提高双缸同步控制精度,各科研机构做了相关研究[2]。李栓柱等[3]为了提高双缸锻造液压机的同步控制精度,设计了免疫神经网络PID控制器,该控制器具有同步跟踪误差小、鲁棒性高等优势。裴红蕾等[4]设计了由内环压力控制和外环位置控制级联的二级控制器以提高重型锻造液压机同步控制精度,该控制器具有很高的位置控制精度且鲁棒性很好。管国栋等[5]针对80 MN锻造液压机采用了西门子PLC与Trio控制器相结合的方案,该方案获得了预期控制效果。董春芳等[6]设计了一种交叉耦合同步控制方式,通过通道状态比较,其双缸同步控制精度较高。HEARNS G等[7]采用定量反馈理论(QFT),并将此应用到双液压缸驱动轧机设备中,控制效果较好。SUN等[8]提出了一种非线性同步控制算法用于双缸同步控制。MASTELLONE S等[9]基于李雅普诺夫稳定性理论,采用主从控制方法,实现机器人的协同工作。王燕等[10]采用电液伺服阀,设计了电液同步多通道加载系统。上海市隧道工程采用液压同步顶进技术,利用PID控制器实现对液压泵驱动电机的控制,通过调节液压泵输出流量,实现位移和压力同步控制[11]。BYUN等[12]提出了一种由2个扰动观测器和1个同步控制器组成的系统,该控制系统降低了扭曲干扰对同步偏差的影响。LI K等[13]采用伪导数反馈方法实现了双液压缸电梯的同步提升,在 400 mm行程中,同步偏差保持在± 2 mm。
对双缸同步控制的研究可以看出,目前针对双液压缸同步控制系统的研究较多,但针对锻造液压机的双缸同步控制系统的研究较少。针对这种情况,本研究设计了锻造液压机双缸同步控制系统,并对系统中双缸同步控制这一关键技术进行研究。采用误差反馈的同步控制结构实现双液压缸同步精确控制,利用遗传算法进行了PID参数整定,为提高锻造液压机双缸同步控制精度提供理论依据。
1 锻造液压机双缸同步控制系统设计
为实现锻造液压机两液压缸高精度同步调整,双缸同步控制系统原理如图1所示设计。两液压缸活塞杆与活动横梁连接,活动横梁垂直运动,实现锻压锻件。
系统具体控制过程可简述为:系统启动后,位移传感器1和2检测此时液压缸1和2的活塞杆位移,并将位移信号反馈给控制器,控制器控制比例阀1和2动作,对液压缸1和2进行油液补充和减小,从而调整液压缸1和2的活塞杆位移,实现其同步控制。
从控制过程可知,系统同步控制精度主要取决于控制器中同步控制策略,此决定着锻造液压机双缸同步控制性能。
2 同步控制系统数学模型建立
由上述系统工作过程可知,为实现高精度的双缸同步控制,关键在于对系统中的液压缸位置进行精确控制。
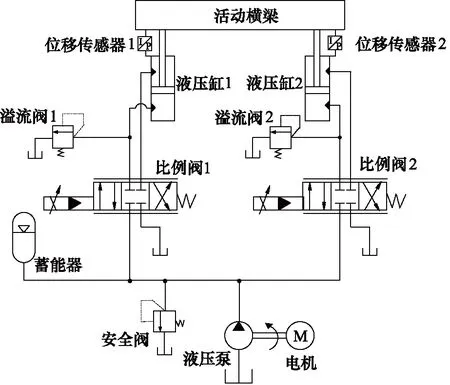
图1 锻造液压机双缸同步控制系统
液压缸位置控制系统原理如图2所示。此系统中主要包括比例放大器、比例方向阀、阀控液压缸系统以及位移传感器[14-16]。
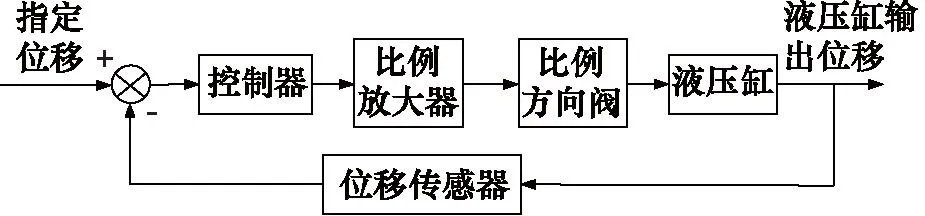
图2 液压缸位置控制系统原理图
液压缸位置控制系统数学建模过程目前采用的方法较为成熟,具体建模过程此处不详细介绍,下面将各环节的数学模型列出。比例放大器数学模型为:
i=KaΔu
(1)
式中,Δu—— 比例放大器输入电压,V
i—— 比例放大器输出电流,A
Ka—— 比例放大器放大系数,A/V
比例方向阀传递函数为[17]:
(2)
式中,Xv—— 比例方向阀阀芯位移,m
Kb—— 比例阀阀芯位移与电流增益系数,m/A
wm—— 比例方向阀固有频率,rad/s
ξm—— 比例方向阀阻尼比
采用了非对称液压缸,非对称液压缸有杆腔和无杆腔有效作用面积不相等,因此液压缸活塞杆伸出和缩回的数学模型不相同[18]。活塞杆伸出时活塞杆位移Xp对比例阀阀芯位移Xv的传递函数为:
(3)
式中,Kq1—— 比例阀流量增益,m2/s
A1—— 无杆腔有效作用面积,m2
wh1—— 活塞杆缩回时液压固有频率,rad/s
ξh1—— 液压阻尼比
活塞杆缩回时活塞杆位移Xp对比例阀阀芯位移Xv的传递函数为:
(4)
式中,Kq2—— 比例阀流量增益,m2/s
A2—— 有杆腔有效作用面积,m2
wh2—— 活塞杆缩回时液压固有频率,rad/s
ξh2—— 液压阻尼比
位移传感器数学模型为:
uf=KfXp
(5)
式中,Kf—— 位置反馈增益,V/m
uf—— 位移传感器反馈电压,V
Xp—— 液压缸输出位移,m
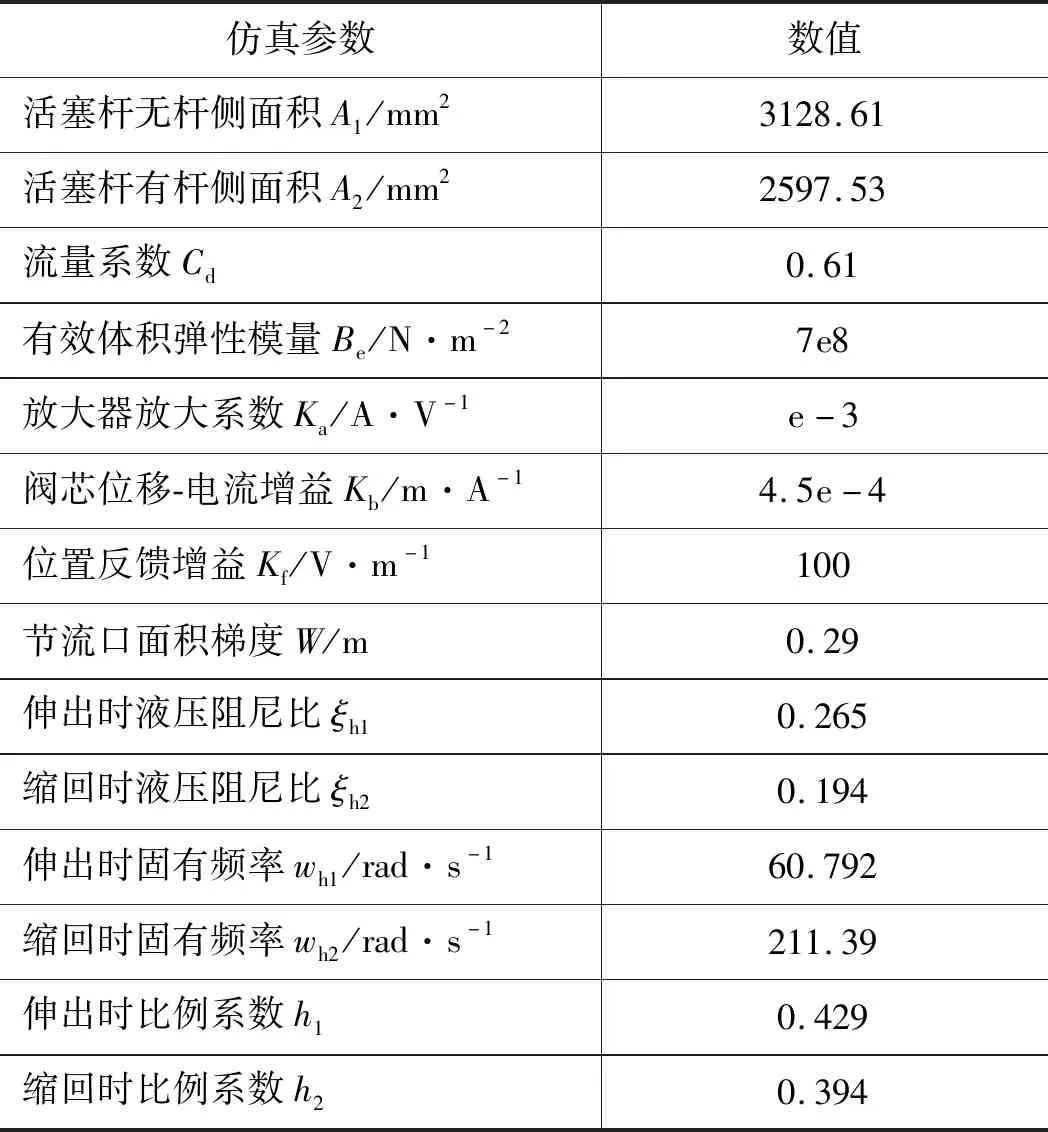
表1 技术参数
系统主要技术参数如表1所示,将参数代入式(3)、式(4),得到活塞杆伸出状态下活塞位移Xp对比例阀阀芯位移Xv的传递函数为:
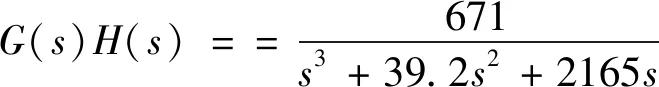
(6)
活塞杆缩回状态下活塞位移Xp对比例阀阀芯位移Xv的传递函数为:
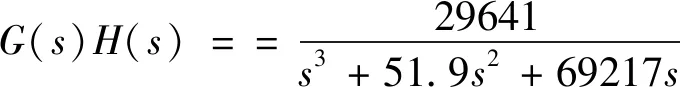
(7)
3 双缸同步控制系统控制策略研究
目前,“串联型”和“并联型”同步控制结构在同步系统中较为常用[19]。“串联型”控制结构如图3所示。“并联型”控制结构如图4所示。
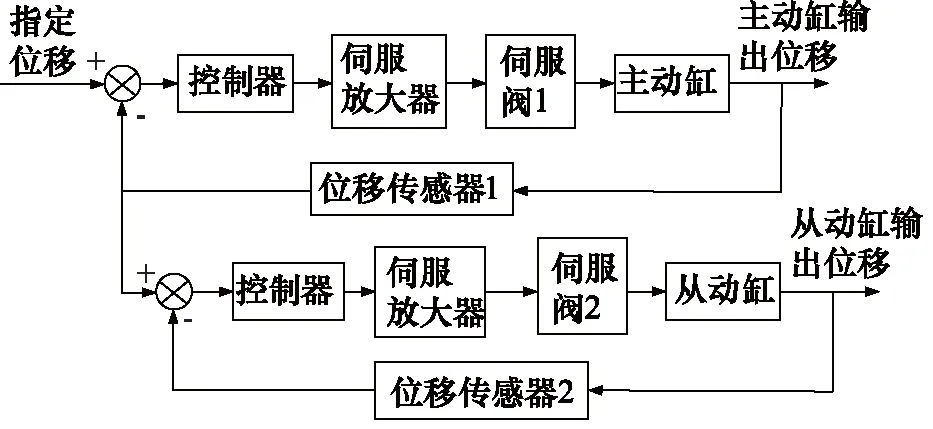
图3 “串联型”同步控制结构
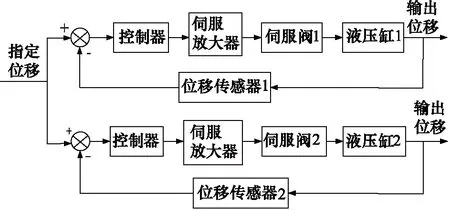
图4 “并联型”同步控制结构
为验证“串联型”和“并联型”同步控制结构控制效果,在MATLAB/Simulink中建立仿真模型,并且控制器采用PID控制器。
首先采用遗传算法实现对PID参数的整定。系统采用种群规模为n=50,交叉概率为pc=0.9,变异概率为pm=0.2,最大迭代次数N=500进行遗传迭代寻优。采用时间误差绝对值积分性能指标(ITAE)作为参数寻优的适应度函数,如式(8):
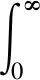
(8)
经过500代进化,可获得液压缸活塞杆2种状态下参数整定结果,如表2和表3所示。
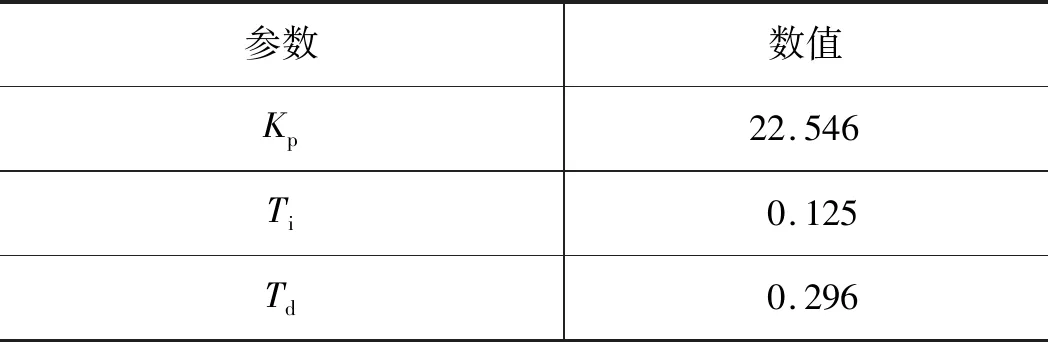
表2 活塞杆伸出时参数整定结果
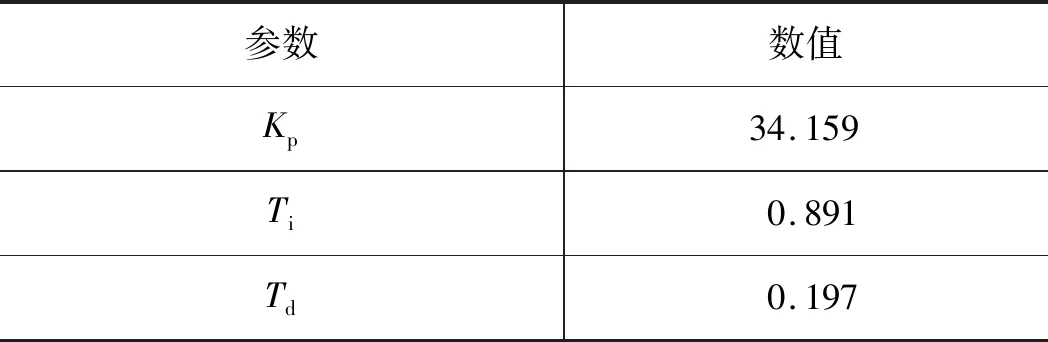
表3 活塞杆缩回时参数整定结果
对系统施加阶跃信号,活塞杆伸出状态下运行仿真结果如图5~图8所示。不同控制结构下仿真结果对比如表4所示。
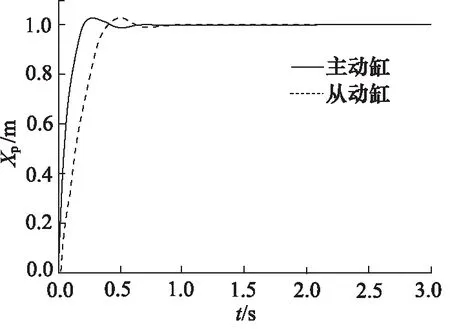
图5 “串联型”控制阶跃响应曲线(活塞杆伸出)
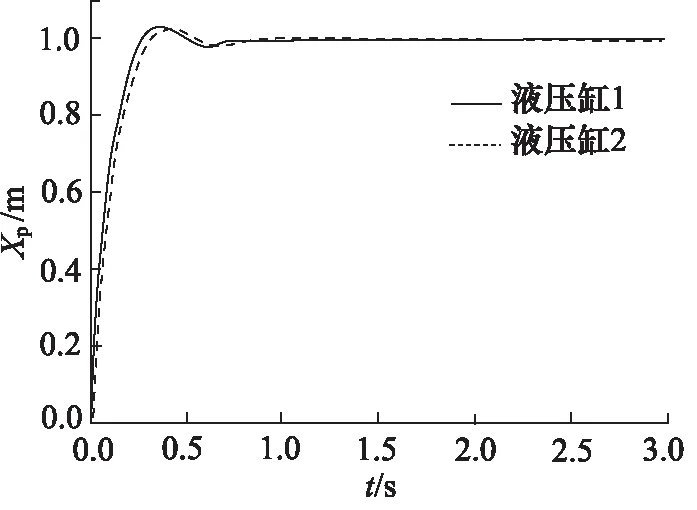
图6 “并联型”控制阶跃响应曲线(活塞杆伸出)
由表4可得,在活塞杆伸出状态下,“并联型”相比“串联型”最大同步误差减小了80.35%;达到稳态同步误差的调整时间增加了28.42%;串联型存在0.001 m的稳态同步误差,而并联型稳态同步误差为0。
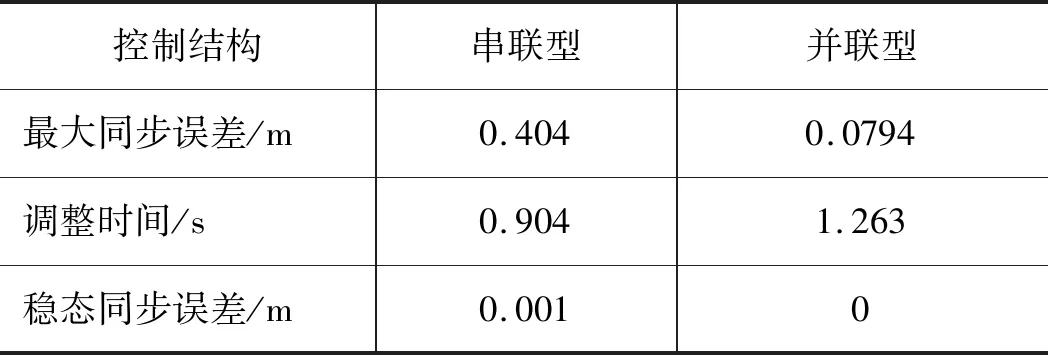
表4 两种结构下仿真结果对比(活塞杆伸出)
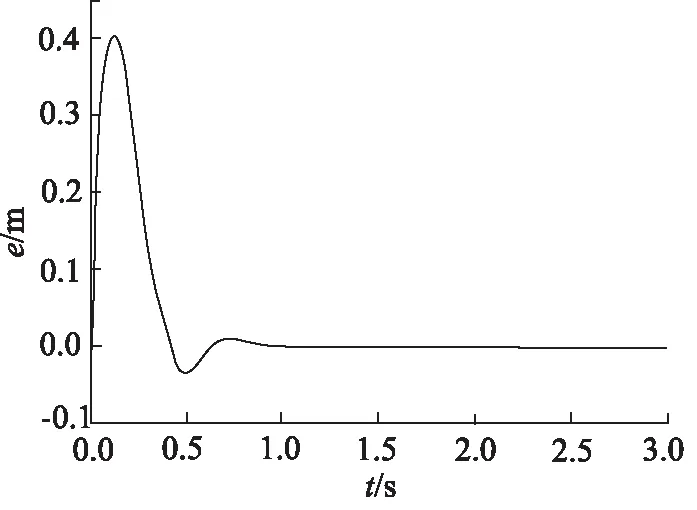
图7 “串联型”控制同步误差(活塞杆伸出)
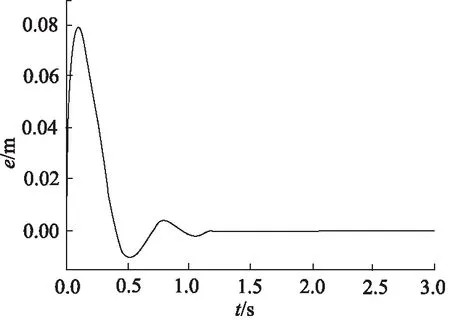
图8 “并联型”控制同步误差(活塞杆伸出)
同样的,对系统施加阶跃信号,阶跃后的值设置为-1,活塞杆缩回状态下运行仿真结果如图9~图12所示。
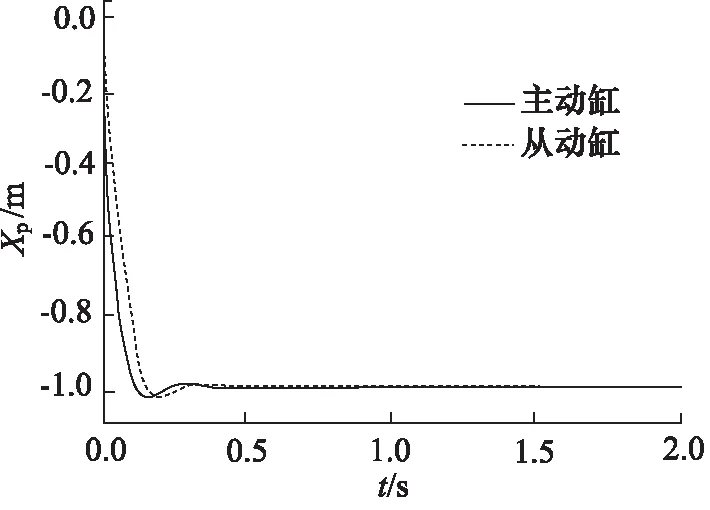
图9 “串联型”控制阶跃响应曲线(活塞杆缩回)
不同控制结构下仿真结果对比,如表5所示。
由表5可得,在活塞杆缩回状态下,“并联型”相比“串联型”最大同步误差减小了88.03%;达到稳态同步误差的调整时间增加了22.12%;2种控制结构下稳态同步误差都为0。
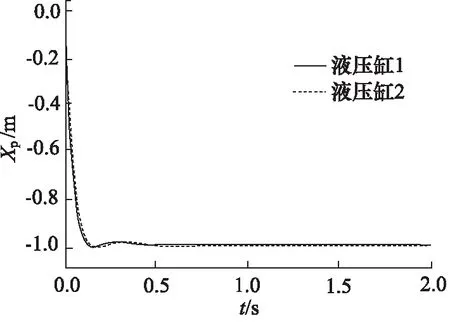
图10 “并联型”控制阶跃响应曲线(活塞杆缩回)
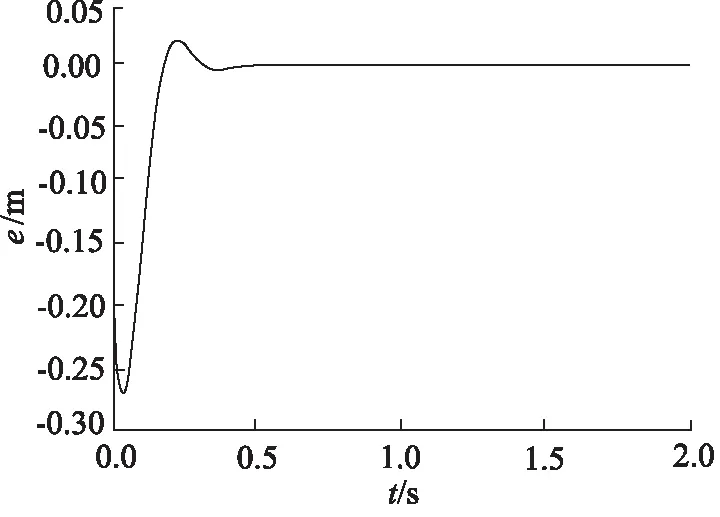
图11 “串联型”控制同步误差(活塞杆缩回)
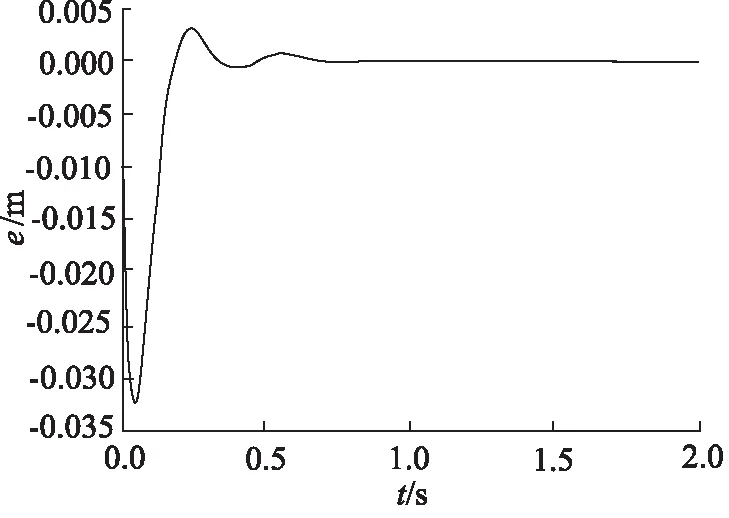
图12 “并联型”控制同步误差(活塞杆缩回)
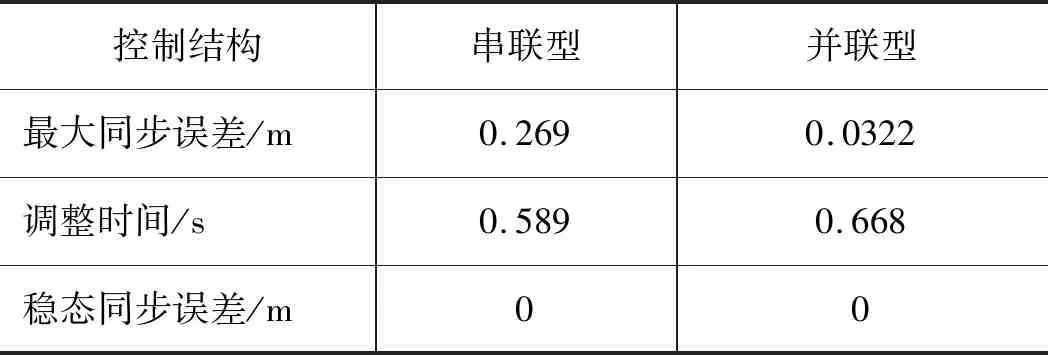
表5 2种结构下仿真结果对比(活塞杆缩回)
分析以上仿真结果可知,“并联型”对于最大同步误差的控制效果优于“串联型”,但“并联型”达到稳态同步误差的调整时间长于“串联型”,因此2种控制结构均存在缺点,无法满足锻造液压机对于同步控制精度的要求。
为提高同步控制精度,采用一种误差反馈的同步控制结构,如图13所示。该控制结构在“串、并联”控制结构的基础之上,将液压缸2的输出位移与液压缸1的输出位移进行比较,并将同步误差补偿给反应速度较慢的液压缸2使其动态响应加快,2缸位移差值减小,从而提高同步控制精度。
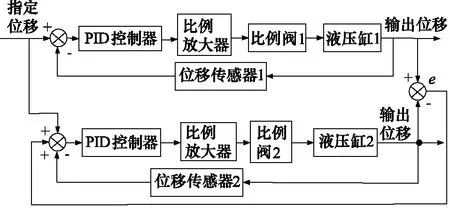
图13 误差反馈的同步控制结构
对系统施加阶跃信号,活塞杆伸出状态下2液压缸阶跃响应曲线和其同步误差如图14和图15所示。
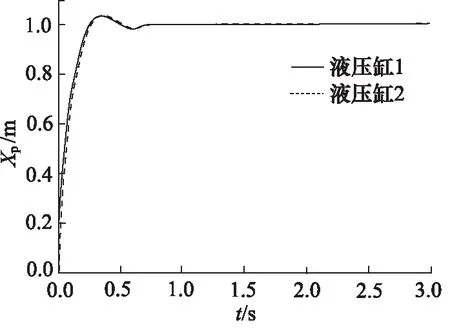
图14 误差反馈控制阶跃响应曲线(活塞杆伸出)
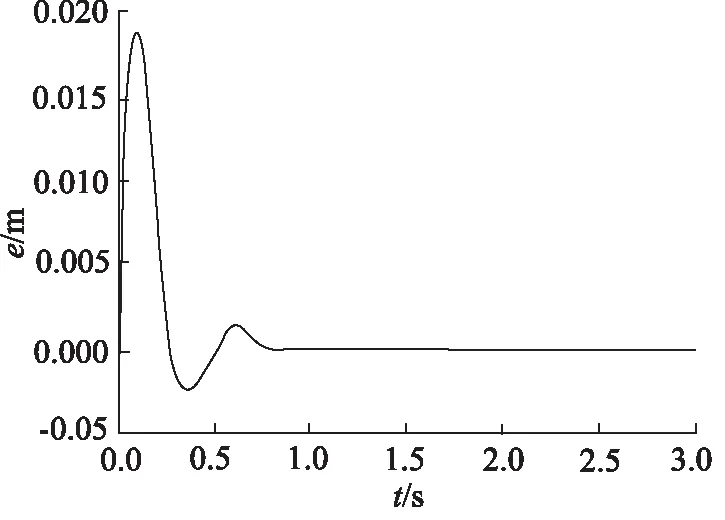
图15 误差反馈控制同步误差(活塞杆伸出)
同样的,对其系统施加阶跃信号,活塞杆缩回状态下2液压缸的阶跃响应曲线和其同步误差如图16和图17所示。
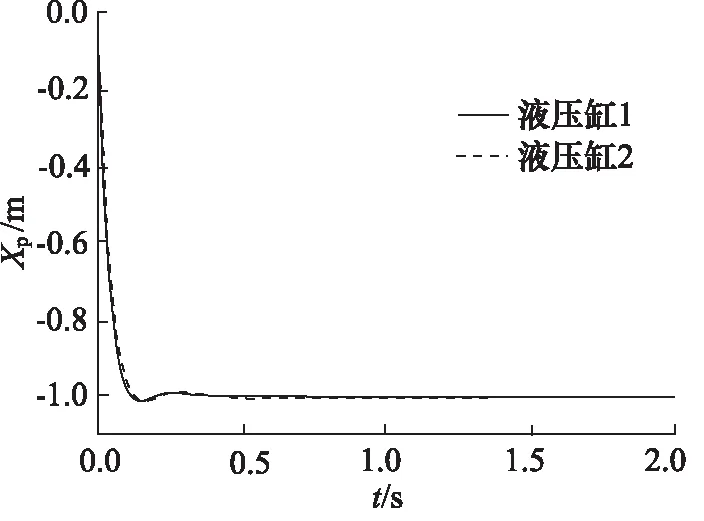
图16 误差反馈控制阶跃响应曲线(活塞杆缩回)
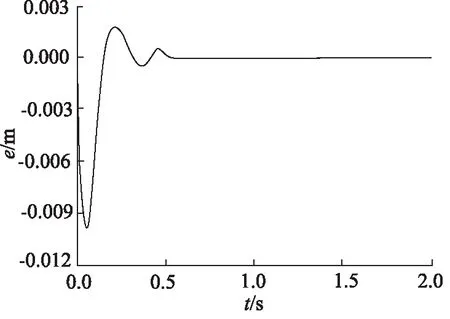
图17 误差反馈控制同步误差(活塞杆缩回)
2种活塞杆状态下系统性能指标,如表6所示。
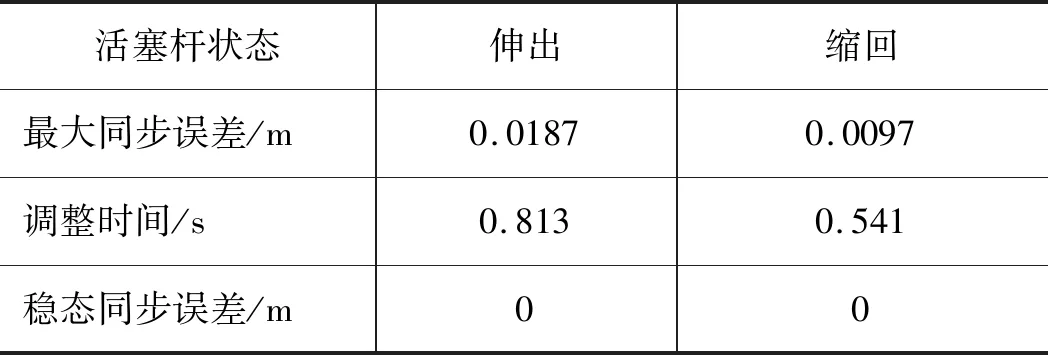
表6 2种活塞杆状态下系统性能指标
由表4~表6可得,在活塞杆伸出状态下,所采用同步控制结构相比“串联型”和“并联型”控制结构最大同步误差分别减小了95.37%和76.42%;达到稳态同步误差的调整时间分别缩短了18.94%和39.51%。在活塞杆缩回状态下,误差反馈同步控制结构相比“串联型”和“并联型”控制结构最大同步误差分别减小了96.39%和69.94%;达到稳态同步误差的调整时间分别缩短了7.36%和19.61%。并且伸出和缩回状态下的稳态误差均为0。从以上数据对比看出,采用同步控制结构能够满足锻造液压机同步控制要求。
4 结论
为实现锻造液压机双缸的同步精确调整,设计了锻造液压机双缸同步控制系统。在“串、并联”控制结构基础之上,采用了误差反馈的同步控制结构,将仿真结果与“串、并联”控制结构仿真结果进行了对比,主要得出以下结论:
在活塞杆伸出状态下,误差反馈同步控制结构相比“串联型”和“并联型”控制结构最大同步误差分别减小了95.37%和76.42%;达到稳态同步误差的调整时间分别缩短了18.94%和39.51%;稳态同步误差分别减小了93.51%和85.40%。在活塞杆缩回状态下,误差反馈控制结构相比“串联型”和“并联型”最大同步误差分别减小了96.39%和69.94%;达到稳态同步误差的调整时间分别缩短了7.36%和19.61%;稳态同步误差分别减小了87.23%和71.15%。从以上数据对比看出,采用同步控制结构能够满足锻造液压机同步控制要求。
