基于图形评审技术的云工作流调度计划风险评价模型
2020-07-14
(内蒙古财经大学 计算机信息管理学院,内蒙古 呼和浩特 010070)
云计算是一种以最小的管理代价快速提供按需计算、存储资源的范式,具有弹性、可扩展等技术优势,可以有效地解决复杂的科学计算问题。云计算所具有的分布式、动态性和虚拟化的特点,导致服务质量(QoS)受到诸多不确定因素的影响。承担工作流计算和存储任务的是运行在物理主机上的多个虚拟机,这些虚拟机共享物理主机的硬件资源,它们之间进行的通信会引发虚拟机性能指标的波动[1],使得云实例的性能未达到预期[2]。然而,现有的服务选择模型和算法较少考虑这类QoS随时间变化所呈现的不确定性特征,使得模型和算法的选择结果不准确,因此解决不确定性QoS感知服务组合问题具有现实意义。
当随机变量的概率分布可以通过计算或者统计的方法获得时,概率分布是云工作流调度的通用方法。已有学者开始关注这种不确定性建模的问题。近几年,概率理论和统计方法已经被应用在云计算工作流调度领域中,以处理多种不确定性因素[3]。在这种方法中,诸如运行时间、任务到达时间、中央处理器(CPU)性能等不确定因素都被建模为已知概率分布函数的随机变量。文献[4]中提出了一种最小化工作流执行时间的随机启发式调度算法,假设任务的执行时间是独立的、满足正态分布的随机变量。文献[5]中使用概率数据流图(PDFG)的方法对不确定云计算环境下工作流调度任务进行建模,使得调度方案能够在运行时间约束下满足指定的置信度概率。在不确定的可用网络带宽环境下,文献[6]中提出了一种不确定带宽值背景下的调度算法,在保证云工作流运行时间最短的情况下,对于非精确输入信息具有更好的鲁棒性。文献[7]中基于虚拟服务节点可用性和负载的不确定性,分别使用Type-Ⅰ和Type-Ⅱ模糊逻辑系统预测资源的可用性和工作负载,提高虚拟数据中心的运行效率。文献[8]中基于历史数据给出了2个度量云工作流执行鲁棒性的度量指标,在假设已知所有数据概率分布的情况下,提出了一种鲁棒性工作流调度和资源分配算法。文献[9]中考虑时间和成本约束下,讨论了运行在基础设施即服务(IaaS)云平台上具有统一分布的相互之间关联的一组工作流不确定性问题。文献[10]中使用蒙特卡洛方法处理工作流执行任务的不确定性。
然而,真实运行的场景不能总是获得足够的信息来表征随机变量参数的概率分布函数。需要使用不同的方法对这种不确定进行建模。文献[11]中提出了一种混沌遗传算法用以解决存在冲突和依赖关系的Web服务组合问题,该算法应用混沌理论、修复策略、新适应度函数等解决局部最优并加快训练速度,但该方法并未考虑不确定性问题。文献[12]中用区间数理论建模QoS的不确定性,采用基于分解的非确定性多目标进化算法解决建模的区间数多目标优化问题。文献[13]中将区间数不确定QoS感知问题转化为具有全局QoS约束的多目标问题,采用新的遗传编码模式解决再编码问题。文献[14]中考虑了工作流活动无法精确估计分布情况下执行时间的不确定特征,提出了一种包含执行时间、费用和鲁棒性3个优化目标的多目标工作流调度算法(R-MOHEFT),能够计算调度方案的帕累托最优集,从而减少执行时间的波动性的影响。文献[15]中使用了区间数描述云计算环境的不确定性,提出了一种可以减少不确定性对云数据中心任务调度质量影响的新的调度架构和算法,基于工作负荷的情况,采用3种动态调度资源策略提高云数据中心的资源使用效率,减少能源消耗。
尽管目前计算生物学和经济学决策领域中对于不确定性问题进行了广泛研究,但是云计算领域的不确定性问题研究内容还比较少,在资源和服务提供以及规划模型等问题中的不确定性因素还没有得到充分地研究[16]。综合现有的研究成果,云计算环境下的工作流调度应用中的不确定性因素会对工作流的执行结果和效率产生显著影响,对这种不确定性进行准确建模可以提高云计算环境下工作流的运行质量。考虑到区间数作为不确定性建模可以不用预先获得随机变量的概率分布函数的优势,不同于现有研究区间数不确定性建模研究,把工作流中的任务集的不确定性看成是独立、静态的过程,本文中基于风险元传递理论对这种不确定性的动态特征进行建模,通过评价不同工作流的调度方案的整体风险,以期获得更好的云计算工作流调度方案的选择结果。
1 模型构建
1.1 云工作流模型
定义1 云工作流。云计算环境下的工作流可以被建模为有向无环图(DAG),可以表示成一个四元组G=〈V,E,t0,tn〉,由下列几个部分组成:
1)V是节点的有限集合。每个节点关联云计算环境下工作流的某个任务ti(0≤i≤n),当工作流开始运行时,可以选择分布在不同区域上的云服务运行。
2)E⊂V×V是顶点之间关联的边。集合中的每个边e=〈ti,pi,tj〉∈E可以表示为三元组,代表云工作流中2个任务之间的依赖关系,pi表示2个任务之间的转移概率,如果某个任务只有一个后继节点,则pi=1。
3)t0∈V表示开始任务;tn∈V表示终止任务。
定义2 执行路径和调度方案。对于一个云工作流的规划T={t1,t2,…,tm},其对应的云组合方案S={S1,S2,…,Sm}为m个备选的调度方案。Q={Q1,Q2,…,Qn}为S中n个QoS指标的集合。
定义3 云工作流QoS风险元。云工作流调度方案中所依赖的各项QoS指标会因各种因素而表现为波动的现象,具有不确定性的特征,称为云工作流QoS风险元。由于该风险元概率分布难于估计,因此采用区间数的方法表示风险元的不确定性度量。
1.2 云工作流多风险元传递模型
图形评审技术(GERT)是一种基于计划评估和审查技术(PERT)通用的随机网络分析方法,已经广泛应用在社会的各个领域。文献[17]中使用GERT分析方法提出了一种复杂供应链的风险分析模型。文献[18]中基于系统耦合理论和极大熵方法提出了一种危险耦合传导图形评审技术改进模型,求解装备活动中危险耦合传导的危险度。文献[19]中构建了可靠性GERT随机网络模型以计算多元件复杂系统可靠度。可见,GERT不仅可以表征风险、不确定等因素,而且其具备的对系统动态、传递特性计算的优点,还可以对云工作流的风险元的动态特性进行建模。
云服务分散在不同地理区域,通过实现业务活动的工作流连接在一起,形成了一个复杂的GERT网络。云工作流QoS风险元依附于工作流中的任务节点,通过信息关联在云工作流之间形成了风险的流动和传递。
基于以上分析,提出的云工作流QoS风险元GERT网络模型如图1所示。

Rij表示节点i与j之间的风险流;pij表示枝线eij的转移概率;是云工作流应用中节点i到j的n个相互独立的风险元。图1 云工作流服务质量风险元图形评审技术网络模型
定义4 云工作流QoS风险元传递GERT网络模型(CQRETM)。CQRETM可以定义为一个三元组。具体的描述为:
1)N={n1,n2,…}表示只包含“或”型节点的风险元传递节点。
2)E={eij|〈vi,vj〉}表示连接顶点的枝线集合。
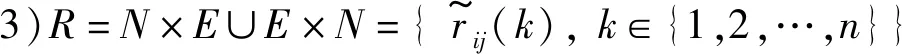
在图1所示的模型中,pij是风险元之间传递能力的度量,表示风险元之间依赖程度和风险发生的程度,等同于传统GERT网络中活动实现概率。
1.3 风险元传递函数的构建
风险元传递函数在建模云工作流QoS风险的动态特征方面具有重要作用。基于等价的风险元传递函数,等价矩母函数和重要的相关参数可以进一步被确定和计算。
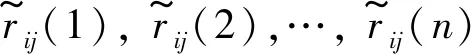
(1)


(2)
根据GERT网络的性质,可以得到如下不同性质。
性质1 当CQRETM的2个节点之间是串联结构的时候,其等价传递函数为串联结构各活动之积,即
性质2 当CQRETM的2个节点之间是并联结构的时候,其等价传递函数为串联结构各活动之和,即
性质3 CQRETM网络自环结构活动的等价传递函数为

(3)

2 工作流QoS风险元传递GERT网络模型解析求解
2.1 云工作流QoS指标区间值
随着云计算中时间约束的应用增多,对服务的执行时间的管理的需求也急剧增长[20]。云环境下,云工作流对于云服务的选择需要在执行时间和其他QoS指标中进行平衡,对执行时间的有效控制可以提供更好的服务[21]。根据云模型理论,逆向云发生器可以实现定量信息向定性概念的转换,生成以(Ex,En,He)为数字特征的定性概念的云模型,其中Ex为时间样本期望值,En为服务执行时间的熵,He为服务执行时间的超熵。为了确定云工作流调用服务执行时间的区间范围,基于云模型理论和切比雪夫不等式,提出如下的时间区间生成算法。
输入:服务执行时间的样本数据{t1,t2,…,tn}。
输出:服务执行时间区间。
5)根据切比雪夫不等式,计算置信度为λ的执行时间区间
对于其他QoS指标的区间值,也可以根据该算法进行计算。
2.2 等价传递概率及等价矩母函数的建立

根据风险元矩母函数的特征可知,当sk=0时,
根据梅森公式,从节点u到节点v的风险元矩母函数为
(4)
2.3 风险度的计算

(5)
本文中的主要目标是评价云工作流调度方案的动态风险。下面给出的云工作流调度方案风险度的概念,可以用来度量因为风险因素导致的云服务QoS不确定性的大小。

风险度RS的计算过程如下。
首先,分别计算调度方案S的风险元一阶矩求解期望值
E[R(k)]=
然后,计算n阶矩求解方差
E[R(k)2]=
可以得到调度方案风险流的方差。
2.4 风险度的比较方法

P(Ri≥Rj)=
(6)
式中P(Ri≥Rj)+P(Rj≥Ri)=1。
计算区间可能度矩阵
PM=(Pij)m×m,
式中Pij=P(Ri≥Rj)。
下面给出风险度的得分函数Score(Ri),以此作为排序的依据。
(7)
式中m表示可能的调度方案个数。得分函数值越大,说明风险元的波动区间越大,意味着更多的不确定性。
3 算例分析
3.1 有效性验证
下面模拟小规模的云工作流调度计划,共11个节点,有5个调度方案S={S1,S2,S3,S4,S5},评价其云工作流QoS风险度。不失一般性,本文中考虑2种QoS指标,即执行时间T、服务费用C的不确定性,对于其他云工作流QoS风险元也可以进行扩展。当这些不确定因素发生时,云工作流服务质量会产生波动影响。模拟运算的结果如图2所示。
利用区间数的除法运算法则,可以得到调度方案S1的风险度R1=[0.01,0.113]。
同理可得

调度方案图2 云工作流调度模拟运算结果
R2=[0.07,0.180],R3=[0.05,0.279],
R4=[0.03,0.135],R5=[0.03,0.083]。
根据公式(7),计算得各个风险度区间数的得分为
Score(R1)=0.285 3,Score(R2)=0.313 3,
Score(R3)=0.338 5,Score(R4)=0.295 8,
Score(R5)=0.267 1。
从而得到各个方案的风险从大到小排序结果为R3、R2、R4、R1、R5。
从各个调度方案的数据区间可以看出,S3所有任务节点的执行时间和运行成本区间范围都是最大的,计算得到的风险度得分也是最高的。同理,S2和S4的风险度得分也与时间和成本区间范围变化一致,说明了本文中提出的方法可以有效地度量区间波动范围产生的不确定性。
3.2 方法对比
QoS的不确定性使得服务选择的结果与最初的期望发生偏离,最终导致整个工作流任务失败。本文中选择均值-方差(E-V)[21]和逼近理想解排序法(TOPSIS)2种模型进行对比,从成功率[22]维度进行比较分析。本文中选择文献[23]中所提供的集成Web服务的旅游业务流为例,业务流上的每个业务节点备选的服务规模选择为10~50个服务。每次实验均进行20次,对结果进行平均值计算,结果如图3所示。
从图可以看出,随着候选服务的数量增多,本文中提出的CQRETM方法的服务选择成功率明显高于E-V方法和TOPSIS方法的,主要原因是通过云模型对云服务历史数据数字特征的构建,计算整个工作流包含的不确定性,通过选择不确定性更少的服务组合,提高了整个工作流执行的成功率。

E-V—均值-方差模型;TOPSIS—逼近理想解排序法;CQRETM—云工作流服务质量风险无图形评审技术网络模型。图3 不同方法的服务选择成功率对比
4 结语
随着云计算基础设施的完善和应用场景的扩展,越来越多的业务迁移到云环境下。云环境下异构、动态的特点,使得云工作流的执行面临诸多的风险因素,各项QoS指标包含诸多的不确定性。为了度量这种不确定性,评价各个云工作流的调度方案的风险大小,本文中提出了一种工作流QoS风险元传递GERT网络模型,基于给出的计算QoS指标区间范围算法,对提出的网络模型构建了传递函数,求解了等价传递概率和矩母函数,并给出了计算工作流调度方案风险度的公式及其比较方法,最后案例说明了本文中提出的方法是可行的。
