基于Steger算子的非平稳信号瞬时频率估计方法

(1.石家庄铁道大学 a.电气与电子工程学院，b.省部共建交通工程结构力学行为与系统安全国家重点实验室，河北 石家庄 050043；2.邯郸学院 机电学院，河北 邯郸 056005)

瞬时频率作为非平稳信号分析的重要参数[1]，已经广泛应用于桥梁振动检测、地震勘测、机械、电力系统、雷达、通信、医学等各方面。变转速工况故障轴承振动信号作为典型的非平稳信号[2]，包含机械设备的瞬态状况以及设备实时运行状态。在一些大型机械设备的故障诊断时无法安装测速装置，只能从振动信号中提取瞬时转频信号，而从时频分布图中精确地估计瞬时频率是时频分析的重要一步。

近几年来，在瞬时频率估计方面提出许多方法，其中最简单的时频脊提取算法属于峰值检测法[3]，但是该法最容易受噪声成分干扰。文献[4-5]中针对连续小波变换得到的时间-尺度平面，采用具有时频点幅值和相邻点频率波动的2项约束建立代价函数提取时频脊。文献[6]中针对时频面提出了与其建立代价函数相似的脊线搜索法。为了避免对初始搜索点位置的限制，文献[3]中也利用相同的代价函数建立了双向时频脊搜索算法。代价函数通常只利用了相邻时频点信息，一旦时频面局部位置出现强噪声或干扰分量的影响，很容易造成脊线提取失效。小波脊线提取方法[7]也常用于脊线提取，对单分量或多分量信号中能量较高的分量提取效果较好，但是对于多分量信号中能量较弱的分量难以识别。

为此，本文中介绍一种新的瞬时频率提取方法。该方法利用二维时频分布图中时频脊线能量分布特点，引入图像处理中Steger算子进行时频谱中瞬时频率脊线提取；通过仿真实验，验证本方法在多分量信号瞬时频率估计方面的精度以及适应性、抗噪性。

1 原理介绍

1.1 时频脊线特点

时频分析是研究非平稳信号的主要工具，其中时频脊线是瞬时频率提取的关键信息。短时傅里叶变换(STFT)作为时频分析最经典的方法之一，对非平稳信号x(t)，在线性空间可测、平方可积x(t)∈L2(R)，定义式为

(1)

式中:Fx(t,ω)为信号的X(t)的短时傅里叶变换,其中t为时间，ω为角频率；gt,ω(τ)为窗函数短时傅里叶变换，τ为时间点；g(τ-t)为窗函数。

在时间方向，取窗函数g(τ-t)与原始信号x(t)相乘，然后进行傅里叶变换；窗函数在时间轴上平移，完成对整个信号的短时傅里叶变换。傅里叶变换将时域信号转化为频域信号，通过幅值谱、相位谱和功率谱来描述信号的频率特征。

短时傅里叶变换将一维时域信号转换成二维时频空间，表征时间与频率之间的关系。若在时频中加入能量谱密度，即可将二维空间变为三维空间，这样可以直观地描述能量谱密度随时间的变化趋势，以及频率与能量谱密度之间关系。图1为一维时域信号短时傅里叶变换频谱图。由图可以看出，瞬时频率的能量呈山脊状态，山脊的最顶端为能量最大点，即峰值点。能量谱密度是一种概率统计方法，因此时频脊能量服从正态分布。图2为信号时频分布图，它是短时傅里叶变换谱图在时频面上的投影。由图可以看出，在投影过程中，山脊峰值和山脊在时频域中变换为时频脊线，并且时频分布也符合能量谱密度分布。

图1 一维时域信号短时傅里叶变换频谱图

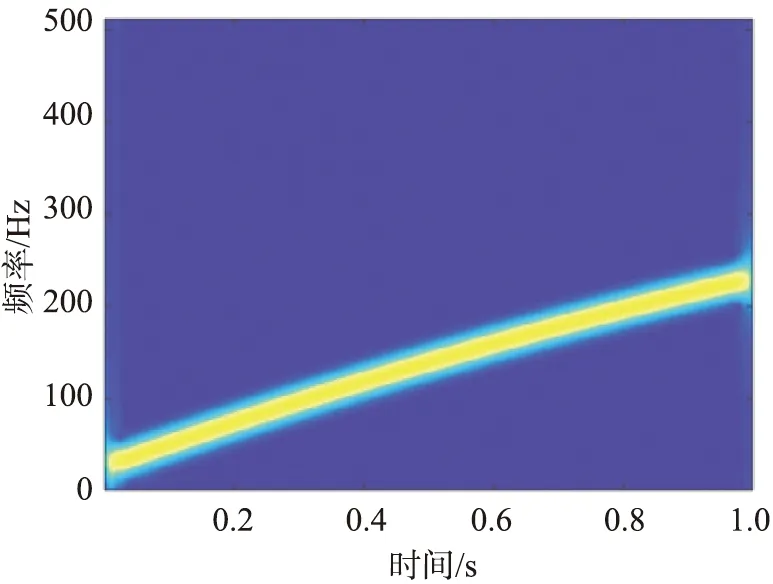
图2 短时傅里叶变换时频分布

1.2 Steger算法原理

在时频聚集性和分辨率较好的时频分布面上，信号的频率切片能量在某一时刻呈现山脉状态，并且服从正态分布。时频脊线边缘能量分布局部最小，脊线峰顶上能量分布局部最大，并且能量最大处为瞬时频率真实值。对时频谱瞬时频率提取是对时频图像中瞬时频率脊线分布局部导数求解，并沿时间方向进行时频脊线的提取，脊线所在位置即为瞬时频率。Steger算法提取时频脊线的具体过程如下。

1.2.1 Gaussian算子平滑滤波

Gaussian算子具有低通滤波特性，是对时频分布图像瞬时频率脊线边缘进行平滑滤波，因此可以通过与Gaussian函数卷积进行平滑滤波。Gaussian算子为

(2)

式中σ为控制滤波平滑性的参数。

将时频图像进行Gaussian算子卷积计算，可使时频分布图像平滑滤波，并且调整参数σ可以控制滤波的平滑性，计算公式为

F(x,y)=G(x,y)*f(x,y)，

(3)

式中：f(x,y)为时频分布图；F(x,y)为卷积后的时频分析图；*为卷积运算符。

1.2.2 构造Hessian矩阵求取时频脊线方向法向量

二维时频分析图的Hessian矩阵H(x,y)可以表示为

(4)

式中rxx、rxy、ryy为时频图像f(x,y)的任意一点的二阶偏导数，可以用Gaussian核函数与时频分析图卷积运算得到。

(5)

式中gxx(x,y)、gxy(x,y)、gyy(x,y)为Gaussian核函数的二阶偏导数，计算公式为

(6)

Hessian矩阵的特征值应与时频图像灰度函数的二阶方向导数的极值对应，并且极值与Hessian矩阵的特征向量方向相同，因此时频图像的法向量(nx,ny)与Hessian矩阵的绝对值最大的特征值的特征向量相等，同时,时频图像函数二阶方向导数也与Hessian矩阵的绝对值最大的特征值相等。

1.2.3 基于亚像素提取时频图脊线

时频二维图像中的某像素(x0,y0)可以用二阶泰勒展开多项式来表示，即

f(x,y)=r(x0,y0)+((x-x0)(y-y0))

(7)

时频二维图像f(x,y)在脊线边缘方向上一阶方向导数值为0，二阶方向导数取极小值点为脊线峰值。通常用(nx,ny)来表示n(x,y)时频边缘方向，因此沿时频脊线边缘方向也可以用(nx,ny)表示，即

f[(tnx+x0),(tny+y0)]=r(x0,y0)+

(8)

针对时频脊线边缘，令

可得

(9)

利用条件(tnx,tny)∈[-0.5,0.5]×[-0.5,0.5]判断一阶导数零点是否位于当前时频像素点，再加上该方向上二阶导数的极小值是否小于阈值，通过这2个判断，就能比较准确地提取时频瞬时脊线的峰值所在时频分布图的位置。最后通过瞬时频率脊线位置与时频分布图位置关系，实现瞬时频率精确估计。

2 算法流程

根据上述分析，本文中提出一种基于Steger算子的非平稳信号瞬时频率估计方法，算法流程如图3所示。具体计算过程如下：

1)将时域非平稳信号进行时频变换得到二维时频分布图；2)对二维时频分布图进行Gaussian算子平滑滤波，增强时频分布图；3)构造Hessian矩阵并求取时频脊线方向法向量；4)对时频脊线进行亚像素提取，得到瞬时频率脊线；5)根据时频分布图像矩阵位置与瞬时频率脊线峰值位置的关系估计瞬时频率。

图3 基于Steger算子的非平稳信号瞬时频率估计算法流程图

3 仿真实验

3.1 多分量仿真信号设计

为了验证Steger算子可以提取多分量信号瞬时频率的适应性，设计复杂的多分量信号s，其中包括2个相位不同的正弦调频信号s1、s2和一个非线性时变信号s3，3个信号叠加组成多分量信号，表达为s(t)=s1(t)+s2(t)+s3(t)，然后再添加Gaussian白噪声，时域波形如图4所示。

(10)

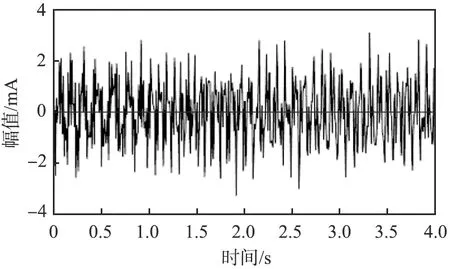
图4 多分量仿真信号时域波形

3.2 适应性

为了验证Steger算子在不同时频谱提取瞬时频率的适应性，信号模型选用多分量信号，并添加Gaussian白噪声，然后对多分量信号分别进行短时傅里叶变换、同步压缩(SST)[8]、时频重排(RS)变换[9]、小波变换得到二维时频分布，如图5所示。

(a)短时傅里叶变换(b)同步压缩(c)时频重排(d)小波变换图5 经过不同方式处理得到的多分量仿真信号时频分布

对上述多分量的二维时频分布图进行Steger算子瞬时频率估计，结果如图6所示。由图可以看出：从短时傅里叶变换时频分布图图6(a)提取的瞬时频率结果来看，可以清晰地看到时频脊线受到噪声的影响，但是在瞬时频率估计时对二维时频分布图进行Gaussian平滑滤波，使得时频脊线锐化，减小了噪声影响，提高瞬时频率估计精度；在同步压缩时频分布图图6(b)提取的瞬时频率结果中，同步压缩是对时频脊线进行挤压，挤压过程受到噪声的影响，使得时频脊线挤压程度发生了变化，瞬时频率曲线出现了变形；在时频重排时频分布图图6(c)提取的瞬时频率结果中，受噪声的影响时频分布图出现毛刺导致瞬时频率曲线出现小的波浪起伏；在小波变换时频分布图图6(d)提取的瞬时频率结果中，时频分布图受小波核函数尺度的影响，在信号瞬时频率变化时，时频分辨率发生明显变化，能量出现发散，使得瞬时频率始端和末端无法估计，但总体上可以精确提取。通过上述分析可知，Steger算子在提取瞬时频率的适应范围比较广泛。

(a)短时傅里叶变换(b)同步压缩(c)时频重排(d)小波变换图6 对不同方法处理得到的时频分布图进行Steger算子瞬时频率估计结果

3.3 抗噪性与估计精度

为了进一步验证基于Steger算子的非平稳信号瞬时频率估计方法在强噪声下估计瞬时频率的抗噪性与精度，并与峰值搜索法进行对比，选用线性调频单分量信号作为仿真信号，仿真信号角频率和模型表达式分别见式(11)、(12)，添加Gaussian白噪声，得到的时域波形如图7所示。

ω(t)=2.5πt+30π，

(11)

(12)

图7 单分量仿真信号时域波形

式中：η(t)为Gaussian白噪声；t为时间，0≤t≤20 s。 将仿真信号进行短时傅里叶变换得到二维时频分布，如图8所示，分别使用本文中提出的方法与峰值搜索法[10-12]进行瞬时频率估计，结果如图9所示。

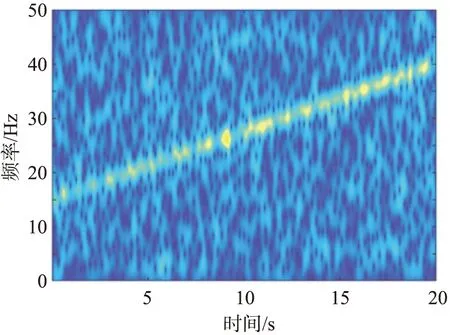
图8 单分量仿真信号时频分布

图9 不同算法的瞬时频率估计结果

从图8中可以看出，由于受到噪声的影响，时频脊线的能量分布发生明显的变化。当使用峰值搜索法时，如果同一时刻受到噪声能量的影响，使时频脊线的峰值能量偏离真实值，将会把时频脊线偏离值作为瞬时频率。采用本文中提出的瞬时频率估计方法，首先进行Gaussian平滑滤波，可以滤除噪声的影响，从而减小误差。从图9中可以明显看出，在受到噪声干扰时，本文中提出的方法的瞬时频率估计结果更接近真实值，表明该方法的抗噪性能明显优于峰值搜索法的。

以下定量分析2种方法在不同信噪比噪声下的瞬时频率估计精度。计算瞬时频率误差率η[8]，

(13)

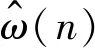
通过大量实验的测试，将上述单分量线性调频信号中加入不同信噪比的Gaussian白噪声，使信噪比为-20～10 dB，并将信号进行短时傅里叶变换得到二维时频分布图。然后分别采用2种方法进行瞬时频率估计，计算2种方法在不同信噪比下瞬时频率估计误差，结果如图10所示。从图中可以看出，本文中提出的方法的瞬时频率误差率小于峰值搜索方法的，且误差率均小于5%，说明该方法具有较高的精度，同时还具有较好的抗噪性。

图10 不同信噪比下不同算法的瞬时频率误差

Rényi熵可以定量分析时频聚集性，是评价时频分辨率的重要指标[13]，Rényi熵越小，时频能量聚集性越好，同时时频分辨率越高。对于维数为α的Rényi熵Hα(X)，当α≥0和α≠1时，定义式为

(14)

式中X为随机变量，对应的概率密度为pi(X=i)，i=1,2,…,n。

对不同Rényi熵的时频分布图，分别采用本文中提出的算法和峰值搜索法进行瞬时频率估计，然后计算2种方法在不同Rényi熵时瞬时频率估计误差[9]，结果如图11所示。从图中可以看出，本文中提出的方法的瞬时频率误差率均明显小于5%，远远小于峰值搜索方法的。

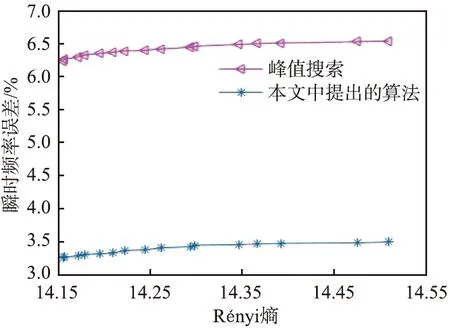
图11 采用不同算法时不同Rényi熵的时频分布的瞬时频率误差

4 实测信号分析

为了进一步验证本文中提出的基于Steger算子的非平稳信号瞬时频率估计方法的实用性和有效性，将该方法应用于实验采集的滚动轴承振动信号来进行瞬时转频估计。采用QPZZ-Ⅱ型旋转机械振动及故障模拟实验平台进行实验，采用NI PXIe 4496型数据采集设备进行数据采集，加速度振动传感器采样频率为25.6 kHz，参考轴转速传感器为激光转速计，采样频率为1 kHz。根据激光转速计采集的信号，采用五点式公式求解真实转频，并与估计的瞬时转频进行比较。为了充分验证方法的有效性，对升速振动信号进行分析。实验滚动轴承的型号为N205EM，有外圈故障，该滚动轴承有关参数见表1。

表1 N205EM型滚动轴承的基本参数

模拟启动工况，转速由升速过程过渡到匀速过程，采样时间为10 s，升速过程转频从11.4 Hz增大到24.6 Hz。原始信号时域波形如图12所示。

图12 实测振动信号的时域波形

实验采集到的振动信号包含轴承故障冲击分量，且转速信号为低频信号。为了提高运算速率并有效提取低频转速信息，首先对采集的振动信号进行低通滤波处理，低通滤波截止频率为1 300 Hz，然后进行降采样处理，其倍数为5。对预处理的振动信号进行小波变换得到二维时频分布，如图13所示。

将得到小波时频分布图进行Steger算子提取瞬时转频，由于受到倍频的影响，因此从图13中可以明显看出倍频分量；但是，由于倍频的能量低于实际转频能量，因此在使用Steger算子时，倍频的虚假分量可以被Gaussian平滑滤波滤除，从而减少倍频分量的影响。最终得到瞬时转频估计结果如图14所示。从图中可以直观地看出，采用本文中提出的方法得到的转频曲线完全与实际转频曲线重合，计算得到的估计误差率为1.32%，表明该方法在瞬时频率估计方面具有较高的精度，并且对倍频的抗噪性效果非常好。

图13 实测振动信号的小波时频分布

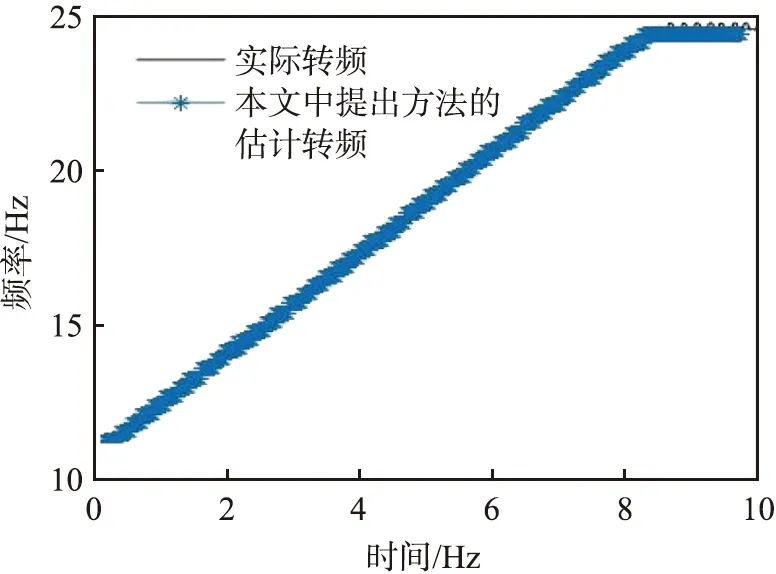
图14 实测振动信号的瞬时转频估计结果

5 结论

1)本文中理论和实验验证了Steger算子能够准确进行瞬时频率估计，提供了一种新颖的瞬时频率估计方法，并且验证了该方法在瞬时频率估计时对时频分布的适应性、抗噪性、精确性良好。

2)本文中提出的方法对时频分布图适应性强，抗噪性优，具有独特的优势。该方法可用于无法安装转速传感器的机械传动装置，通过采集振动信息进行瞬时转频估计，将瞬时转频作为后期进行多阶比分析重要环节，对滚动轴承故障诊断具有重要意义。

3)在恶劣工况下，机械振动信息中包含强背景噪声和很多的干扰成分，在利用本文中提出的方法进行瞬时频率估计时，需要先得到高分辨率和清晰的时频分布图，这样才能获得高精度的瞬时频率。