电站载物爬楼机器人的动态稳定性建模与控制

胡安超，佃松宜，赵 涛

(四川大学电气工程学院，成都 610065)

爬楼机器人因具有结构简单、操作容易等优点，可作为残疾人上下楼、货物运输等场景的移动平台，因此很多学者针对其建模、控制与优化等方面进行研究。目前，人们已研制出多种类型的爬楼机器人，如轮式、履带式、复合式[1]等。其中，履带式机器人不易打滑、重心变化小、直线运动效果较好、适用范围较广[2-3]，因此，基于履带式机器人进行研究。在上下楼过程中，由于楼梯倾斜角度及其他因素的变化，会使机器人的重心和俯仰角产生相应的改变。为了防止机器人在爬楼过程中发生倾翻、载物滑落等意外现象，须通过控制系统调节爬楼机器人的重心位置，维持其动态稳定和平衡。

针对爬楼机器人动态稳定性的控制问题，文献[4]根据倾角变化，利用电机控制曲柄滑块机构，进而实现对机器人倾角的控制；文献[5]介绍了一种凸轮结构，以补偿运动单元旋转过程中对轮椅稳定性产生的波动；文献[6]通过4个连杆机构连接至轮椅基座，利用平行四边形特性保持基座水平；文献[7]介绍了爬楼轮椅的台阶攀登和轴定位过程之间相互独立的关系，简化了同步过程，进而更好地通过连杆使轮椅保持平衡；文献[8]提出的结构由6根连杆、丝杠和导轨组成，通过控制滚珠丝杠来调节座椅重心和相对水平轴的角度位置；文献[9]提出关节式履带机器人与楼梯一点、两点和多点接触的一种动态稳定性准则判别方法，并建立动力学方程。

为了确保爬楼机器人能安全、稳定地爬楼，关于爬楼机器人的动态稳定性问题，归纳出机器人的运动模式并建立数学模型。结合量子粒子群优化(quantum particle swarm optimization，QPSO) 算法优化的一型模糊逻辑控制器(1 type of fuzzy logic，1T1FLC)对爬楼机器人的动态稳定性进行控制，并将其与比例-积分-微分(proportion-integral-derivative, PID)、T1FLC及粒子群优化算法(particles swarm optimization, PSO)优化的T1FLC进行对比，观察QPSO-T1FLC方法的控制效果。与现有研究方法相比，主要创新点如下：①归纳出机器人的运动模式，利用几何关系和运动学关系构建被控对象的数学模型；②根据爬楼机器人上下两部分的重心距离与期望距离间的误差、误差变化率及电动推杆伸缩量的关系，设计动态稳定性控制系统的T1FLC；③针对模糊规则参数难以确定的问题，采用QPSO优化隶属度函数参数。

1 电站载物爬楼机器人

研究对象是针对电站工件运输所设计的载物爬楼机器人，结构如图1所示。该载物爬楼机器人的结构由行走单元、稳定性调节单元、运输平台等部件组成。行走单元负责执行上、下楼的基本动作；稳定性调节单元通过控制电动推杆的伸缩量来调节机器人的重心位置；运输平台用于装载工件等。

图1 电站载物爬楼机器人结构Fig.1 Power station load climbing robot structure

电站载物爬楼机器人的整个爬楼过程可以分为4个阶段，如图2所示。

图2 爬楼过程Fig.2 Climbing processes

图2中，履带与水平轴的夹角θ1变化如式(1)～式(4)所示。

过程1：

(1)

过程2：

(L1-v1t)sinθ2=b

(2)

过程3：

(3)

过程4：

(4)

式中：θ1为长履带部分与水平轴间夹角；θ2为运输平台与履带间夹角；θ3为短履带部分与水平轴间夹角；θ4为楼梯斜平面与水平轴间夹角；L1、L2分别为长履带和短履带的长度；L3为履带前端伸出楼梯的长度；h为履带前端至楼梯的垂直高度；a、b分别为楼梯的宽度和高度；v1为履带前进、后退速度。

2 爬楼机器人的动态稳定性建模与分析

假设机器人在上、下楼过程中：楼梯不发生形变；两侧履带运动状态一致；履带与楼梯之间没有发生相对滑动造成机器人转向等意外情况。

2.1 爬楼稳定性条件

假设机器人整体模型如图3所示，在爬楼过程中履带的中心轴线与地面夹角不断变大，重心不断升高和前移。

图3 机器人成功攀爬楼梯Fig.3 Robot successfully climbs the stairs

以楼梯的尖角A点为支点，履带翻越楼梯的条件可用式(5)描述：

(T1P1)Δt+wL*<(GP2)Δt

(5)

式(5)中：T1为履带推力；G为机器人整体重力；P1、P2分别为T1、G对A点的力臂；w为履带抬起的角速度；L*为转动惯量。由式(5)可知，在爬楼过程中，机器人整体的重心G与履带翻越支点A保持在一条垂直线上或者重心G靠后，即P2≥0时，载物爬楼机器人能够保持动态稳定，不会发生倾翻、货物滑落现象。

2.2 建模与分析

为了研究方便，将电站载物爬楼机器人的模型抽象为上下两部分。上部分表示运输平台，依靠中间的电动推杆调节状态；下部分表示履带。考虑到运输货物置放位置，分3种情况进行建模分析。

情况1：运输平台的重心位于中间时，受力情况如图4所示。机器人坐标系XOY位于机器人履带的左下端支点，XiOiYi、XwOwYw均是履带左上端支点的坐标系。机器人上部分质量为m1；下部分质量为m2；l1、l2分别为上下两部分的长度；h1、h2分别为上下两部分的高度；L、L′均为G1、G2在坐标系XOY下横坐标之间的距离；上部分、下部分和机器人整体的重心分别位于G1(x1,y1)、G2(x2,y2)、G3(x3,y3)。

图4 情况1Fig.4 Situation one

在坐标系XOY下：

(6)

(7)

L=x1-x2

(8)

式(8)中：L=0为期望值。

L′=x′1-x′2

(9)

ΔL=L-L′

(10)

(11)

(12)

根据式(13)、式(14)可得运输平台转动的角度θ2。

(13)

(14)

式(14)为机器人整体重心G3的约束条件；Hmax、Hmin分别为重心G3高度的上下限值。

根据式(15)可得电动推杆的输出量为

(15)

式(15)中：l4、l5和l分别表示运输平台旋转支点至电动推杆首端距离、运输平台旋转支点至电动推杆尾端距离、电动推杆总长度。

情况2：运输平台的重心位于后端时，L>0为期望值。由于情况2和情况1类似，所以不再具体分析该情况。

情况3：运输平台的重心位于前端时，L<0为期望值。根据分析，电动推杆需要很大的量程才能保证G1、G2共线，同时在实际过程中，该情况易发生倾翻现象，因此不考虑该情况。

根据式(6)～式(15),可得电站载物爬楼机器人的动态稳定非线性模型，如式(16)和式(17)所示。

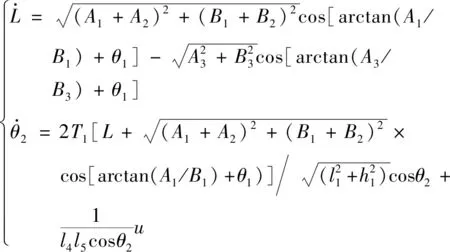
(16)

式(16)中：

(17)

3 量子粒子群优化算法原理

3.1 标准粒子群优化算法

PSO[10-11]是一种基于群体的随机优化技术，已广泛应用于各种优化问题。在粒子群优化算法中，每个粒子都代表优化问题的一个潜在解。假设在D维的优化空间中，粒子群的规模为N，则在t时刻第i个粒子的位置表示为Xi(t)=[Xi,1(t),Xi,2(t),…,Xi,D(t)]，第i个粒子的速度可表示为Vi(t)=[Vi,1(t),Vi,2(t),…,Vi,D(t)]，第i个粒子当前最优位置记为Pi(t)=[Pi,1,Pi,2,…,Pi,D],种群最优位置记为G(t)=[Pg,1,Pg,2,…,Pg,D]，其中1≤g≤N。第i个粒子的最优位置可由式(18)确定，即

(18)

种群最优位置可由式(19)确定，即

(19)

标准粒子群第i个粒子的速度和位置更新可由式(20)确定，即

(20)

式(20)中：w为非负数的惯性因子；c1表示粒子飞向自身最好位置的因子；c2为粒子飞向全局最好位置的因子；r1和r2为(0,1)上均匀分布的随机数。由于粒子在搜索最优位置时，存在飞离搜索范围的潜在风险，所以为了降低粒子飞离空间的概率，需要对粒子的速度和位置进行限制，即

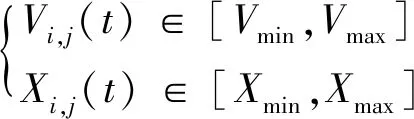
(21)

3.2 量子粒子群优化算法

针对PSO算法依赖于速度-位移轨道模型及全局寻优能力不足的缺陷，文献[12-14]提出了QPSO算法。与标准PSO算法相比，QPSO算法内的粒子以概率密度函数来表示其真实的状态，同时引入了粒子的平均最好位置，在整个优化空间中寻找最优解，因此QPSO算法是一种优于PSO的优化算法。

在QPSO算法中，粒子的量子态通过波函数来描述，具体粒子位置的更新方式由式(22)确定，即

(22)

式(22)中：ui,j和φj均表示为[0,1]上均匀分布的随机数；Li,j由式(23)确定，即

Li,j(t+1)=2β|m-xi,j(t)|

(23)

式(23)中：β表示收缩-扩张系数，通常可以选取固定值或者随着迭代次数增加呈现线性递减的规律，β=1-0.5(iter/item)。其中：m表示粒子群个体最优位置Pi(t)的平均值，由式(24)确定；iter表示当前粒子的迭代次数，而item表示为粒子群最大迭代次数。

(24)

4 模糊控制器的设计及优化

4.1 模糊控制器设计

本节设计模糊控制器进而实现电站载物爬楼机器人系统的动态稳定性。

根据电站载物爬楼机器人的非线性模型[式(16)～式(17)]，定义输出跟踪误差：

e(k)=Lr(k)-L(k)

(25)

式(25)中：Lr(k)是机器人上下两部分重心距离差值的期望值；L(k)是系统输出值。

模糊控制器采取if-then形式来描述非线性系统，对于多输入单输出(multi-input single-output, MISO)系统，电站载物爬楼机器人控制系统的模糊规则为

(26)

规则前件中e∈[-3,3]表示系统输出值与期望值之间的偏差值，ec∈[-3,3]表示系统输出值与期望值之间的偏差变化率；规则后件中u∈[-1.5,+1.5]表示模糊控制器的输出，即电动推杆的伸缩速度。

电站载物爬楼机器人动态稳定性控制系统的整体原理图如图5所示。

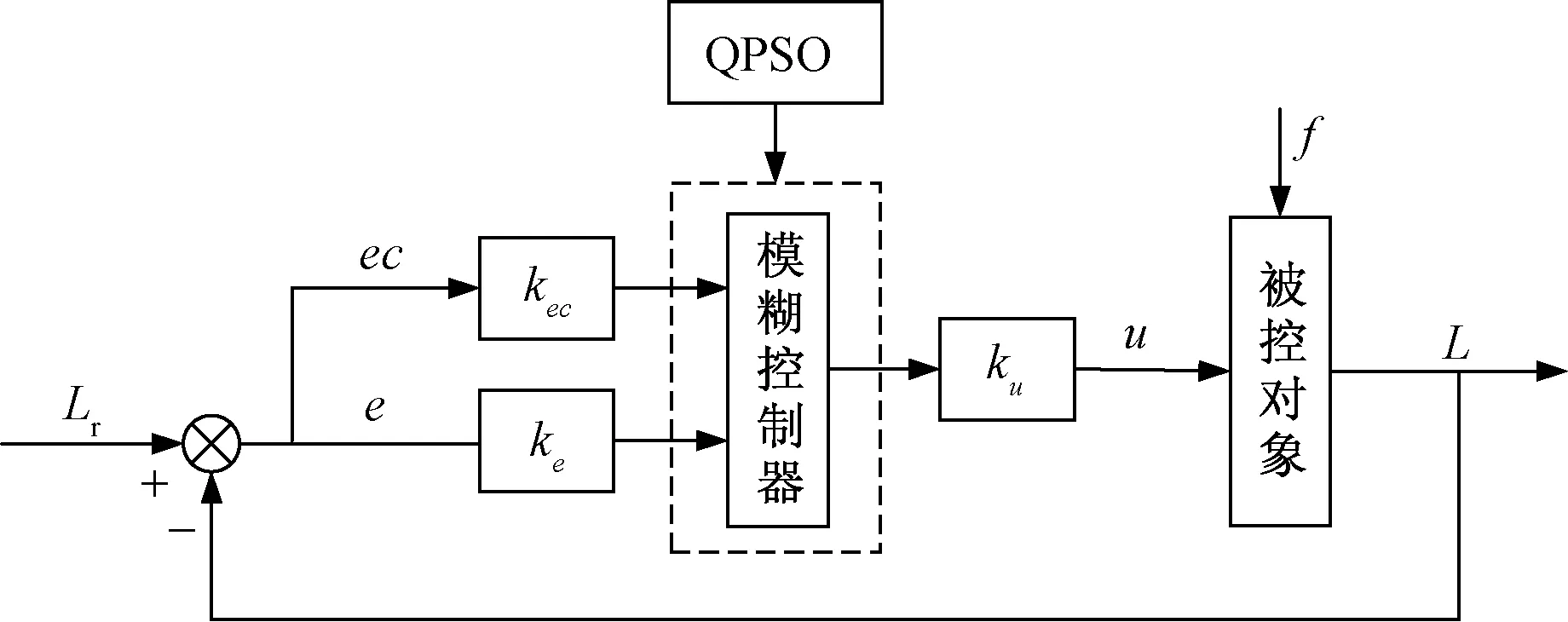
图5 动态稳定性控制系统原理图Fig.5 Dynamic stability control system schematic

图5中：ke与kec是量化因子，将输入量的基本论域转化为模糊论域；ku是比例因子，将输出量的模糊论域转换为基本论域；f表示外部干扰。

设定输入前件和输出后件的模糊子集为{负大、负中、负小、零、正小、正中、正大}，简记为{NB,NM,NS,ZO,PS,PM,PB}。选择三角形函数分别作为输入、输出的隶属度函数，控制器模糊推理的类型为Mamdani，去模糊类型为Centroid。确定了7×7模糊规则表，具体如表1所示。

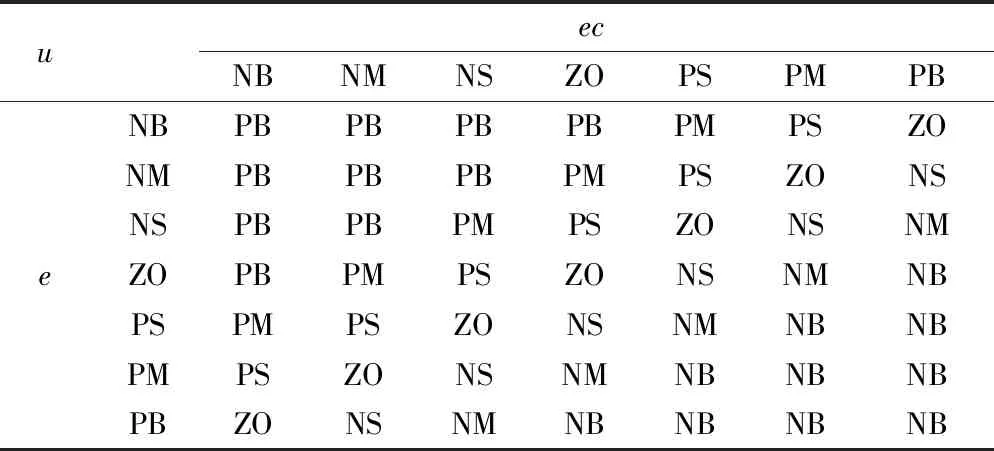
表1 系统稳定性控制模糊规则表Table 1 System stability control fuzzy rule table

4.2 模糊隶属度函数优化

隶属度函数参数一般根据专家知识及现场操作经验进行选择，过程繁琐，因此针对一个强耦合非线性系统，所设计的控制器很难达到最佳的控制效果。为了获取更好的控制器性能，利用QPSO算法对模糊控制器的隶属度函数参数进行优化。

在优化参数时，适应度函数用来衡量每个个体的优良程度是QPSO算法的关键。种群个体进入下一代的概率由适应度的大小所决定，越优良的个体，其适应度值也越大。为了提高控制器的性能，QPSO算法的适应度函数采用时间和误差绝对值的积分(ITAE)作为最小目标函数，即

(27)

式(27)中：λ为计算步长。

QPSO算法的优化步骤如下。

第1步：初始化粒子种群，即设置粒子群规模数为N且每个粒子有D维，令X={X1,X2,…,XD}，设置最大迭代数k、因子c1和c2。

第2步：设置收缩-扩张系数β、个体最优位置Pi(0)、种群最优位置G(0)，设置t=0。

第3步：将每个粒子代入控制器中进行控制、求解，根据式(18)计算粒子群当前平均最优位置及位置适应值。

第4步：根据式(19)计算种群最优位置，根据式(22)更新当前粒子的位置，设置t=t+1。

第5步：判断是否达到迭代次数，若是，进行下一步；否则，返回至第3步。

第6步：输出优化后的模糊隶属度函数参数。

5 仿真结果与分析

针对电站载物爬楼机器人的动态稳定性模型，采用QPSO后的模糊逻辑控制器对其进行控制。为了更好地说明模型的正确性与控制器的有效性，分别对QPSO的T1FLC、PSO优化的T1FLC、未优化的T1FLC及位置式PID控制效果进行仿真对比。

位置式PID控制算法如下：

(28)

式(28)中：Kp、Ki和Kd分别代表比例、积分和微分。经过大量试凑，得出3个参数值为Kp=0.08、Ki=0.04、Kd=0.1。

机器人系统相关参数如表2所示。

表2 电站载物爬楼机器人相关参数Table 2 Power station load-climbing robot related parameters

QPSO前/后的前件、后件隶属度函数分别如图6(a)、图6(b)所示。

图6 控制器的前件、后件隶属度函数Fig.6 Controller’s front and rear membership functions

根据式(1)～式(4)，可得到机器人履带与水平轴夹角θ1及θ1增量变化曲线如图7、图8所示。

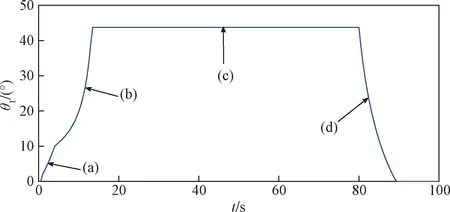
图7 机器人履带与水平轴夹角变化曲线Fig.7 The curve of the angle between the robot track and the horizontal axis

图8 机器人履带与水平轴夹角增量变化曲线Fig.8 The incremental curve of the angle between the robot track and the horizontal axis

图7中，(a)、(b)、(c)、(d)段分别表示机器人在爬楼第1、2、3、4阶段θ1角度变化的趋势。

为了研究方便，针对时刻改变的θ1及θ1增量，选取L输出值为0和1的方波作为2.2节中情况1和情况2的期望输出。

关于电站爬载物楼机器人动态稳定性的控制，首先在不考虑外界干扰的条件下，对比位置式PID、T1FLC、PSO-T1FLC与QPSO-T1FLC方法的控制效果。

图9所示为电站载物爬楼机器人在无干扰时动态稳定性控制的效果。由图9可知，采用QPSO后的模糊控制方法响应快、超调小、稳定性好。

图9 无干扰时动态稳定性控制Fig.9 Dynamic stability control without interference

考虑到电站载物爬楼机器人会受到外界及自身不确定性因素的影响，在t=155 s时对4种方法均增加了干扰。

图10所示为加入干扰后4种方法的控制输出曲线对比图，从图10中可知，QPSO-T1FLC能以更快的反应速度使系统达到指定位置，抗干扰性能较好。

图10 干扰时动态稳定性控制Fig.10 Dynamic stability control with interference

6 实验验证及分析

为了进一步验证所建模型的准确性及控制优化方法的有效性，进行现场实验，如图11所示。

根据图11可知，在整个爬楼过程中，爬楼机器人均能很好地调节系统稳定性，保证了承载物的安全运输，进一步说明了本文模型及控制方法的合理性。

图11 实验验证Fig.11 Experimental verification

7 结论

针对电站载物爬楼机器人动态稳定性的控制问题，根据系统的特性建立非线性模型，并设计了模糊控制器。针对模糊控制器中隶属度函数的参数难以确定的问题，采用QPSO方式得出最佳值。仿真、实验表明，与位置式PID、T1FLC、PSO-T1FLC方法对比，QPSO-T1FLC控制方法响应速度快、超调小、抗干扰性能更好，同时表明了本文所建非线性模型的准确性和控制优化方法的有效性。