一种安全高效的群签名方案

欧海文 雷亚超 王湘南

1(北京电子科技学院 北京 100070)2(西安电子科技大学通信工程学院 陕西 西安 710071)

0 引 言

群签名作为一种特殊的数字签名，不仅可以实现对签名者的匿名，在必要的时候还可以实现对签名者的追踪。因此，自1991年群签名[1]被提出以来，短时间内就出现了很多经典的群签名方案[2-5]，同时随着应用情况和安全性因素的变化，很多改进方案也相应而生[6-7]。为了进一步提高群签名方案的效率和安全性，2015年白永祥[8]提出了一种高效的群签名方案。2018年，针对白永祥方案不能抵抗合谋攻击的问题，于璇等[9]基于椭圆曲线上的离散对数问题对白永祥的方案进行了改进，虽然增强了其抗合谋攻击的能力，但是改进方案过于繁琐复杂，执行效率较低。

本文通过对这些群签名方案[8-9]进行深入分析和研究，提出了一个安全性无减弱，但签名长度更短、计算复杂度更低的签名方案。该方案首先通过添加随机数的方式打破了公钥状态列表中公钥和私钥的直接联系，规避了被撤销成员联合得出其他成员私钥的风险。其次，考虑到应用过程中私钥泄露所造成的严重后果，在对一些具有前向安全性群签名方案研究[10-13]的基础上，提出了具有下述特点的群成员和群管理员的密钥更新方案：群成员私钥随时间段跨越而自然更新，群中成员不需要重新修改原始密钥，只要使签名方案进入下一个时间段，就可以成功度过危险期，避免因私钥泄露造成的危害。而且在不知道随机数r和a的情况下,方案具有前后向安全性，从而减少了群成员反复注册和修改信息的次数，大大增加了方案在应用时的容错性和稳定性。相较于文献[10-13]，本文通过在签名过程中将私钥更新方案中的变化量间接传递给群管理员，简化了由于私钥变化所造成的复杂的检验过程，而且还不需要借助第三方的参数。

本文研究改进的群签名方案对当今应用广泛的区块链技术也有重要的意义。因为区块链的去中心和不可篡改特性，使得用户的身份和交易信息一旦泄露将是永久性行为，所以当区块链系统中的用户存在密钥泄露时，就会造成不可挽回的永久性损失。由于本文提出的方案中设置了随时间段变化的私钥更新环节，所以当区块链中用户利用该方案进行交易签名确认时，不仅可以在私钥泄露后保证前面所进行交易的安全性，还可以使用户继续进行安全的交易签名，降低了私钥泄露带来的巨大损失。

1 签名方案

由文献[14]可知，存在满足条件的椭圆曲线可构成co-GDH的短签名方案。所以本文利用该理论提出了一种签名长度较短的，具有前向安全性的新的群签名方案。

1.1 系统初始化

选取G1=

,G2=,|G1|=|G2|=p,其中P∈E(Fq),Q∈E(Fqα)。由文献[9]可知，存在对应的非退化的双线性映射e:G1×G2→GT,H:{0,1}*→G1，H1:{0,1}*→Zp,同构映射ψ:G2→G1。

对于GM：取x0∈RZp，计算Y=x0Q∈G2，其中x0为群管理员私钥，Y为公钥。故群公共参数为{p,P,Q,G1,G2,e,H,ψ}，群公钥为Y。

1.2 成员加入

(1) 对于ui，ui取xi,0，ri∈RZp，计算yi=xi,0Q∈G2，Ki=riH(IDi)，Li=riQ，然后将(IDi,yi,Ki,Li)发送给GM。其中IDi代表成员ui的现实身份信息。

(2) 收到(IDi,yi,Ki,Li)后，GM先验证等式e(Ki,Q)=e(H(IDi),Li)是否成立，确认IDi的有效性。即：

e(Ki,Q)=e(riH(IDi),Q)=e(H(IDi),riQ)=e(H(IDi),Li)

若成立，计算：

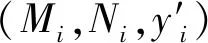
表1 PKSL表

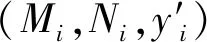
1.3 成员密钥更新

成员密钥泄露在签名中往往会造成严重后果，近年来，为了降低密钥泄露所造成的损失，陆续提出了前向安全、入侵容忍和密钥隔离等技术。这些方法都是以密钥更新为基础。其中密钥隔离技术需要借助协助器进行密钥的更新，而且每次更新都是相互独立的，这将会大幅增加通信成本以及对通信安全性的要求。本文方案主要采用前向安全技术，即通过利用一个单向函数进行密钥的更新。即：

(1) 将整个有效时间划分为若干个时间段1，2，…,L。

(2) 在第j阶段，设群成员ui的密钥为xi,j，群管理员密钥为xj，则第j+1阶段的密钥为：

xi,j+1=xi,j+H1(riP‖j+1)-H1(riP‖j)

xj+1=xj+pH1(aP‖j+1)

式中:ri为ui在申请加入群时选取的随机数，a∈RZp为固定常数。

(3) 在计算出第j+1阶段的密钥后，立即删除第j阶段密钥。

1.4 消息签名

群成员ui对于消息M：

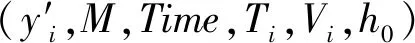
表2 追踪列表

(3)成员ui接收到c后，验证e(c,Q)=e(Ti,Y)是否成立，若成立(c，Time，Ti，Vi)即为群成员ui对于消息M的签名。

1.5 签名验证

验证者在接收到签名(c，Time，Ti，Vi)后，验证e(c,Q)=e(Ti,Y)是否成立，若成立，则接受(c，Time，Ti，Vi)为群成员ui对于消息M的正确的群签名。

1.6 签名打开

1.7 成员撤销

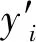
2 正确性与安全性分析

2.1 正确性分析

与文献[9]一样，该方案中的系统建立以及签名过程也存在管理员与成员双向验证身份的过程。

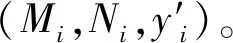
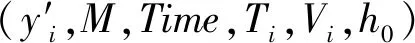
(3) 私钥更新的迭代。对于群中成员的私钥更新方案，即：

因为xi,j+1=xi,j+H1(riP‖j+1)-H1(riP‖j)

所以xi,j+1=xi,j-1+H1(riP‖j)-H1(riP‖j-1)+

H1(riP‖j+1)-H1(riP‖j)=

xi,j-1+H1(riP‖j+1)-H1(riP‖j-1)=

⋮

xi,0+H1(riP‖j+1)-H1(riP‖0)

对于群管理员第j+1阶段私钥：

xj+1=xj+pH1(aP‖j+1)

因为 |G2|=p，G2=

所以xj+1Q=xjQ

由上述推导过程可知，在不泄露随机数ri的情况下，群成员私钥更新方案既具有前向安全性，还具有后向安全性。而对于群管理员，在不泄露随机数a的情况下，满足前向安全性，而且在整个群管理员初始密钥有效的过程中，群公钥不发生改变。

(4) 签名的正确性。首先验证签名(c，Time，Ti，Vi)中的c的正确性，证明签名过程确实有群管理员参与。即验证：e(c,Q)=e(xjTi,Q)=e(Ti,xjQ)=e(Ti,Y)。其次，验证Ti的正确性，即：

Ti=H(M‖Time‖Q‖biQ)=

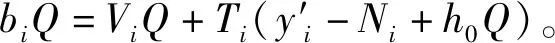
因为Vi=bi-Tixi,j

所以biQ=(Vi+Tixi,j)Q=ViQ+Tixi,jQ=

ViQ+Ti(xi,0+h1-h2)Q=

ViQ+Ti(xi,0Q+h0Q)=

通过上述几个方面的分析，证明了本文所提方案的正确性。

2.2 安全性分析

根据群签名的安全性要求，本文将从以下几个方面论述本文方案的安全性。

(1) 匿名性。接收到签名(c，Time，Ti，Vi)后，验证者只是验证e(c,Q)=e(Ti,Y)是否成立来决定是否接受该签名，其中只用到了群管理员GM的公钥Y，并没有涉及群成员ui的信息。所以，本方案满足匿名性。

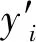
(3) 追踪性。接收到签名(c，Time，Ti，Vi)后，群管理员GM可直接根据Ti、Vi值查找追踪列表，从而追踪到该签名者的身份信息，实现追踪的目的。

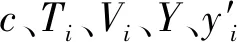
(5) 不可关联性。对任意消息M的签名(c，Time，Ti，Vi)，其中Ti=H(M‖Time‖Q‖biQ)，Vi=bi-Tixi,j，c=xjTi，bi∈RZp，Time是群成员准备进行签名时从可信时间戳机构获得的时间。所以可知签名中的所有成员都是随机的不涉及签名成员信息的，满足不可关联性。

(6) 防陷害性。由上述签名过程可知群管理员和群成员都不能代替他人产生有效的签名。因为无论是群管理员还是群中成员都有秘密保存的私钥，在其不暴露的情况下，该方案都是满足防陷害性的。而且，由Ti=H(M‖Time‖Q‖biQ)，Vi=bi-Tixi,j可知只有知道私钥xi,j的成员才能产生符合Ti=H(M‖Time‖Q‖(ViQ+Tiyi+h0Q))的Ti、Vi,故群中成员可通过验证Ti、Vi的值来防止群管理员冒充自己伪造签名，同时证明群管理员的不可信。

(7) 前向安全性。该签名方案通过构建不改变初始公钥的密钥更新方案，在不同阶段产生不同的私钥值，而且由Hash函数的单向性可知，在不知道随机数ri和a情况下，无法由当前密钥获取之前的密钥。所以即使当前的私钥泄露或丢失，前面阶段所产生的签名仍然是安全的，可被验证的。

(8) 后向安全性。由群成员的私钥更新方案可知，在不知道随机数ri的情况下，无法从当前密钥推之前和之后的密钥。故在群成员当前密钥泄露时，不需要重新选取初始密钥，只需过渡到下一阶段，即可进行安全的签名，避免因私钥泄露造成危害。

3 效率分析

文献[9]基于白永祥方案提出了一种椭圆曲线上的高效安全的实现方案。将本文方案与文献[9]方案从成员加入签名验证的计算复杂度进行比较。综合两个签名方案可知，方案中的主要操作是椭圆曲线上的乘法、双线性映射的计算以及Hash函数的计算，所以本文主要考虑这三种主要操作的数目来衡量签名方案效率。计算复杂度如表3所示。

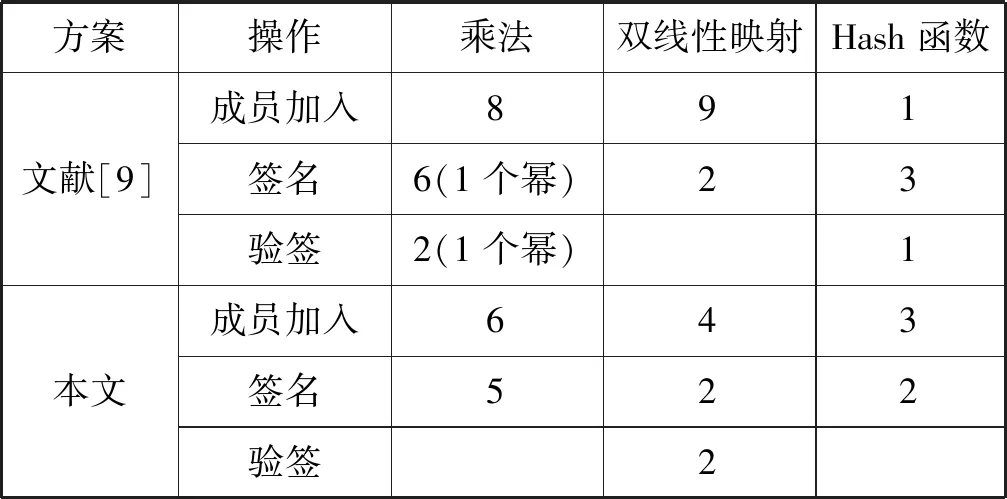
表3 计算复杂度对比表

由表3可知，在保持同样安全性的前提下，本文所提方案的效率远高于文献[9]中方案，而且签名长度也短。同时在实现签名的前向安全性方面，本文方案中设计的密钥更新方案较文献[10-13]也更加简洁，而且还能实现后向安全性。

4 结 语

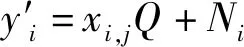
性设计将会更易于本文方案的实际应用，尤其是对于现在应用广泛的区块链技术。下一步，我们将会注重研究群签名的实际应用。