云计算环境下朴素贝叶斯安全分类外包方案研究
2020-07-14陈思
陈 思
(南京理工大学信息化建设与管理处 江苏 南京 210094)
0 引 言
人类、机器、物理世界三元的高度融合引发了数据规模的急速式增长和数据模式的高度复杂化,我们已进入了大数据时代[1]。与此同时,在处理、分析海量数据方面表现良好的机器学习已经成为人工智能领域中的一个重要分支。现机器学习算法主要包括分类、聚类算法,其中分类算法主要包括支持向量机(SVM)、朴素贝叶斯、决策树等,甚至部分神经网络也能完成分类任务。在一个机器学习实例中,主要包括模型训练和模型使用两个阶段,模型训练即利用本地训练集完成模型初始化并进行参数优化,模型使用则是利用训练完成的模型,通过输入特征向量得到分类预测结果。无论是机器学习模型训练还是模型使用都可以看作是一种特殊的计算,且伴随着应用场景的拓展及使用数据量的扩大,这些计算的规模也会剧增,这对于一些本地资源受限的个人用户来说,很难高质量地独立完成。为此我们需要借助云服务器的计算存储能力,实现机器学习模型训练和模型使用的外包。
云计算是一种基于互联网的计算方式,通过这种方式,共享的软硬件资源和信息可以按需求提供给计算机和其他设备,云是网络、互联网的一种比喻说法[2]。外包计算是云计算中最重要的应用之一,指的是一个计算能力有限的客户将任务外包给云中的一个或者多个服务器[3]。这一基于云计算的应用场景正好契合由大规模数据驱动的机器学习模型训练及预测任务。当结合外包计算技术和机器学习实例时,我们常需要借助云服务器的计算存储能力代替用户的本地计算与存储,而这一过程必须考虑数据安全性问题。第一,用于训练机器学习模型的训练数据常常包含其大量个人隐私信息,因此其持有者不希望将明文暴露给其他人;第二,基于云服务器的外包环境具有不确定性,在外包方案中常以半可信状态假设(会推测敏感信息),即云服务器会正确执行用户预设的计算任务,但其会想方设法推测用户的隐私信息而不易被察觉。
在模型训练阶段,主要考虑训练数据集的数据安全问题,例如以疾病预测为目标的机器学习医疗系统,常用的训练数据集是与病患直接关联的诊断数据,极有可能带有大量的隐私信息,这类数据在训练外包过程中往往不能以明文的形式传递。在模型使用阶段,用户通常注重输入实例及最终分类结果的隐私保护,而对于提供分类服务的模型拥有者,由于高精度高鲁棒性的模型常需要大量人力、物力进行训练,因此执行分类外包时模型的明文不能直接发布给远程服务器。如何在保证模型训练及模型使用可行的情况下完成关键数据隔离,是机器学习安全外包主要的研究内容,也是亟需解决的关键问题。
为了解决这个问题,文献[4]针对SVM、朴素贝叶斯和决策树三种分类器的模型训练阶段,通过与AdaBoost迭代算法结合,构建弱分类器并最终组合的方式提出训练过程外包模型,但没有考虑模型使用阶段的应对方法。文献[5]针对支持向量机分类器模型训练及模型使用阶段的安全问题设计了安全外包方案,但该方案不能很好地迁移到朴素贝叶斯分类外包方案中。文献[6]利用差分隐私的思想解决多数据源情况下的朴素贝叶斯模型训练外包的场景,也没有考虑模型使用阶段的外包安全。文献[7]针对朴素贝叶斯分类外包任务,利用私有信息检索技术及同态加密技术实现安全外包,但该方案时空开销较大,不能很好地实际部署与应用。
现如今大多数朴素贝叶斯外包方案多注重模型训练阶段的安全外包,尚没有人考虑模型预测阶段的安全外包。本文首次针对朴素贝叶斯模型分类预测场景,设计实现了一套基于同态加密技术及盲化技术的朴素贝叶斯安全分类外包系统,该系统借助云服务器高效计算存储能力以及随时在线提供分类预测服务的特性,实现了模型的高效、准确分类外包。本文创新点如下:
(1) 允许模型拥有者在本地不限编程语言地训练朴素贝叶斯分类模型,将模型加密委托给半可信的云服务器后可以离线,之后的分类任务将不需要模型拥有者的参与;
(2) 首次针对朴素贝叶斯分类预测阶段,利用同态加密方法及盲化性质设计了朴素贝叶斯安全分类外包方案并基于Java编程语言实现了系统可视化;
(3) 允许用户登陆安全外包系统与云服务器进行交互并在确保隐私的情况下得到安全可靠的分类结果,且支持各类朴素贝叶斯分类实例。
1 朴素贝叶斯安全分类外包原理
1.1 朴素贝叶斯分类器及分类外包
朴素贝叶斯分类是分类预测样本标签的有效算法,朴素贝叶斯分类器的思想原理很简单:给出待分类样本,求出该样本属于某个类别的后验概率,哪个概率最大,就认为此样本属于哪个类别。简要描述朴素贝叶斯分类过程如下:
(1) 设特征向量x={x1,x2,…,xd}为一个待分类项,每一个xi代表x的一个特征属性。
(2) 有类别y={y1,y2,…,yn}。
(3) 计算P(y1|x)、P(y2|x)、…、P(yn|x),即x属于每个类的后验概率。
(4) 若P(yk|x)=max{P(y1|x),…,P(yn|x)},就认为x属于第k类。


先验概率:{P(Y=y1),P(Y=y2),…,P(Y=yn)},其中第i个元素表示x属于yi类的概率。
类条件概率:{P(Xj=v|Y=yi)},它表示x属于yi类时,x的第j个分量为v的概率,其中v属于Xj的值域Sj,i∈[n],j∈[d]。
当有其他用户需要借助训练好的朴素贝叶斯模型进行分类预测问题时,一方面,模型拥有者不希望直接暴露模型明文供其他人任意使用,另一方面,用户不愿暴露自己待预测的特征向量以及最终分类结果。另外,模型拥有者也无法始终保持在线以及同时应对大量用户的预测任务,因此我们考虑基于云计算环境实现朴素贝叶斯分类模型的分类预测外包任务。借助云服务器的计算存储能力,将训练好的模型上传至云服务器后模型拥有者可以离线,使用模型的大量用户可以同时与云服务器交互,输入其特征向量x,服务器结合模型W返回具体分类结果YW(x)。这一过程看似简单,实际上需要考虑多方的数据安全。当引入第三方云服务器代替模型拥有者参与计算时,外包方案需要保证上传的模型以及用户输入的特征向量对云服务器不可见。这一过程中,我们选择引入同态加密这一常用的密码学方案,允许云服务器在密文条件下实现正确分类。
1.2 同态加密技术
同态加密使明文的计算能够在相应密文上执行,且不暴露明文信息。一个非对称同态加密方案AHε支持一般加法及数乘的密文操作。给定两个使用了同一公钥加密的消息AHε.Enc(a)和AHε.Enc(b),存在一个加法操作⊕使得AHε.Enc(a)⊕AHε.Enc(b)的结果解密就是明文a+b的结果。AHε.Enc(a)表示明文a加密的结果,c是一个固定的值,数乘AHε.Enc(ca)满足以下等式:
AHε.Enc(a)⊙…⊙AHε.Enc(a)=AHε.Enc(a)c
由于效率问题,本文使用Paillier同态加密系统,简单介绍如下:
(1) 随机选取两个素数p和q,满足gcd(pq,(p-1)(q-1))=1,gcd(·)求取最大公约数。
(2) 计算n=pq和λ=lcm(p-1,q-1),lcm(·)求取最小公倍数。

(4) 公钥为(n,g),私钥为(λ,u)。
(5) 加密:选择一个随机数r∈(0,n-1],密文即为c=gm·rnmodn2。
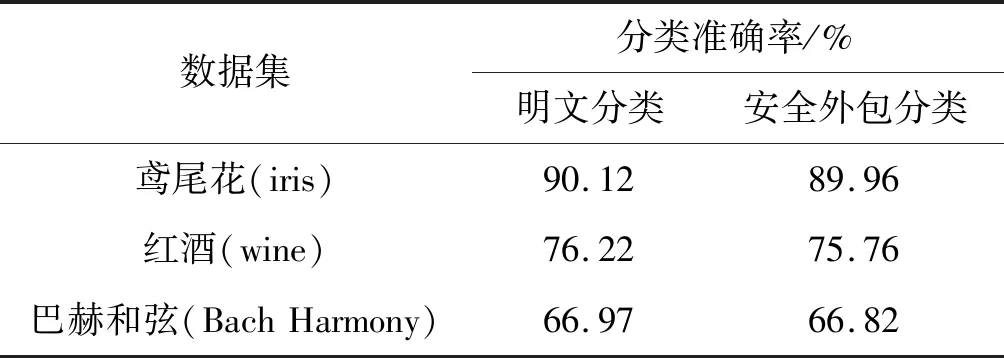
(6) 解密:计算m=L(cλmodn2)·umodn,验证m 作为一种加密工具,同态加密是云计算外包领域最常使用的方法之一。一方面,其同态性质允许我们针对不同的计算场景设计对应的计算方案并确保计算结果的正确性;另一方面,在不知道解密密钥的情况下,加密数据的安全性有严格的保障。本文系统通过引入两套同态加密系统并结合其他的一些密码学工具设计、实现了针对模型、特征向量以及分类结果安全性的保障,真正意义上实现了安全外包。 本文安全外包方案包含模型拥有者、远程服务器、用户(模型使用者)三方实体,方案的整体结构如图1所示。 图1 朴素贝叶斯安全分类外包方案总体结构 由于Paillier加密系统只能对整数进行操作,为了Paillier加密系统能对模型W进行加密,我们通过乘以一个事先给定的大整数L的方式把浮点数表示的概率转化为一个整数(向上取整),转化得到的整数在ZN域中,即Paillier系统的明文空间。整个外包方案使用到两套Paillier同态加密系统 记xj的值域为Sj,其中xj为实例向量的第j个属性。为了在朴素贝叶斯分类器模型W上使用Paillier加密,我们对提取出来的概率模型进行预处理,每种概率的对数用整数表示。 对每一个i∈[n],第i个先验概率为: 对每一个j∈[d],v∈[Sj],类条件概率表示为: P(i,j,v)=|Llog(KP(Xj=v|Y=yi))| 算法1加密后验概率求取算法 用户U输入:特征向量x=(x1,x2,…,xd),私钥sk1,公钥pk1、pk2 远程服务器RS输入:加密模型{E1(P(i))}和{E1(P(i,j,v))},私钥sk2,公钥pk1、pk2 输出:{E2(Pi)}={E2(P(Y=yi,X=x))} fori∈[n]: RS:从ZN1上选择盲化因子Oi,0 forj∈[d]: RS:从ZN1上选择盲化因子Oi,j endfor endfor fori∈[n]: RS:盲化E1(P′(i))=E1(P(i))⊕E1(Oi,0) forj∈[d],v∈[Sj]: RS:盲化E1(P′(i,j,v))=E1(P(i,j,v))⊕E1(Oi,j) endfor endfor 用pk2加密Oi-N1为E2(Oi-N1) 发送E1(P′(i))、E1(P′(i,j,xj))和E2(Oi-N1)给U U:解密E1(P′(i))得到P′(i) 解密E1(P′(i,j,xj))得到P′(i,j,xj) fori∈[n]: endfor 输出加密后验概率{E2(Pi)} 通过算法1我们已将朴素贝叶斯安全分类问题转化为密文条件下的argmax问题,只需要与云服务器交互得到满足argmax{E2{Pi}}的i即可。但在这一步骤中不能直接将E2{Pi}发送给服务器,需要保证拥有解密私钥的远程服务器对最终分类结果不可见,因此我们将再次利用同态性质及盲化技术实现安全双方计算,具体流程如算法2所示。 算法2加密数据求取最大值算法 用户U输入:n个加密后验概率{E2{Pi}},公钥pk2 远程服务器RS输入:私钥sk2 输出:i←arg max{E2{Pi}}U:在[n]上选择一个随机排列π(·) 将{E2{Pi}}按随机排列顺序存放(第i个元素放在π(·)中i所在的位置) 重排密文加入比较队列 队列长度k=n While(k>1): fori∈[k]: 从队列中依次选取元素E2{Pk}和E2{Pk+1},在ZN2上随机选择一个整数r,计算 U将较大元素的密文原文加入新比较队列,重新统计队列长度 end for 当比较队列中只有一个元素时停止交互,得到该元素所在随机排列中的初始数i 输出:最终分类结果i 本文采用面向对象的JavaScript网络脚本语言,内嵌基于Java编程的具体算法,实现了朴素贝叶斯安全分类外包功能及可视化。为了仿真基于云服务器的外包计算环境,我们以多台8 GB内存的Lenovo y400笔记本及一台64 GB内存、Intel(R) Xeon(R) CPU E5-2640 2.60 GHz处理器Windows 8操作系统的Think Server服务器共同组成交互式外包分类环境,借助ThinkServer强大的计算存储能力,实现了单服务器与多用户的一对多访问模式,允许模型拥有者本地训练并加密上传朴素贝叶斯模型至服务器,同时允许多个用户登录系统同时加密访问服务器使用模型完成分类。 本文系统主界面如图2所示,用户注册登录后可以查看使用已发布模型,模型拥有者在图3模型发布界面可以添加模型描述,加密上传模型。图4展示了用户使用模型得到分类预测结果的界面。为了证明本文外包方案适用于多种不同的朴素贝叶斯分类实例,我们选取了三类可使用朴素贝叶斯分类器进行分类预测的数据集:(1) 鸢尾花数据集:通过花萼长度、花萼宽度、花瓣长度、花瓣宽度4个属性预测花卉属于3个种类中哪一类;(2) 红酒数据集:根据红酒的13种成分判断其属于3个种类中哪一类;(3) 巴赫和弦数据集:根据14个和弦属性判断其具体为巴赫哪一个作品。 图2 系统主界面图 图3 模型上传界面图 图4 分类结果显示界面图 本文利用十折交叉验证法对三类数据集分别进行分类预测统计,对比经由密文安全外包分类及明文直接分类两种方式的模型平均准确率,比较结果如表1所示。可以看出,本文外包方案在确保模型隐私、用户输入向量及分类结果隐私的前提下并没有损失过多模型分类准确率(小于1%),且没有影响模型的实用性。分析与明文下测试的模型准确率的差距,主要来源于利用Paillier同态加密方法时,为确保加密成功需要有小数转换为整数的放缩过程,这一过程中的精度损失可以通过调整大整数K的大小进行控制。另外,本文系统允许模型拥有者上传加密模型后离线,服务器的高吞吐量也极大提高了多用户同时进行分类预测的效率。 表1 模型准确率对比 随着云计算的快速发展,外包计算和机器分类学习的结合得到了广泛的关注和应用,现迫切需要设计和实现考虑用户隐私及模型安全的外包分类系统。本文提出的朴素贝叶斯分类系统由分类器模型拥有者、远程服务器以及用户组成,模型拥有者通过远程服务器为用户提供分类服务。本文仿真实现了服务器和用户的交互,得到了相应的分类结果,并对该系统中各个实体所关心的隐私数据通过同态加密或盲化技术实现隔离。结果表明,本文系统在不影响模型分类准确率的情况下实现了对分类器模型隐私性、用户特征向量及分类结果隐私性的保护。2 朴素贝叶斯安全分类外包方案
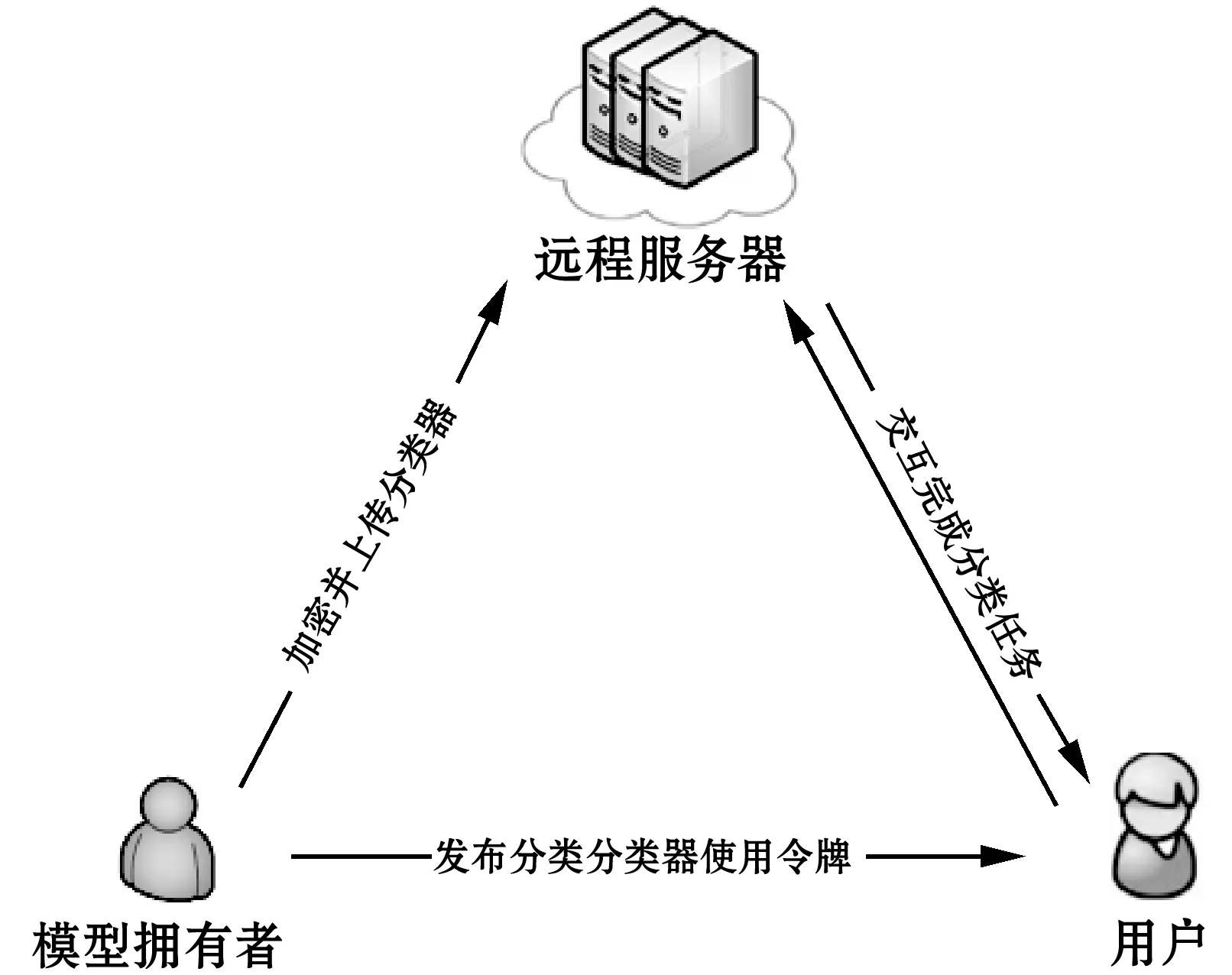
2.1 用户本地训练并加密上传模型
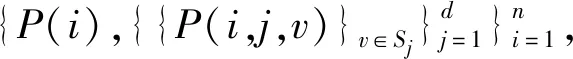
2.2 用户与服务器交互得到加密后验概率
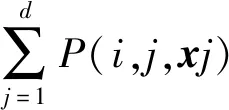
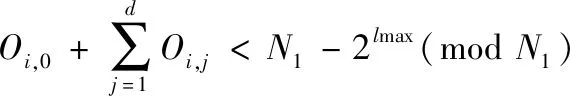
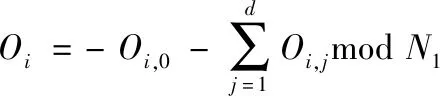
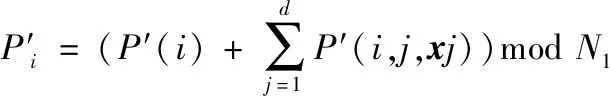
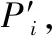
2.3 密文后验概率中求取最终分类结果

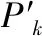
3 系统可视化仿真

4 结 语
