无双线性对的无证书组密钥协商协议的安全性分析及改进
2020-07-14张金辉黄加成梁红梅李慧敏
张金辉 黄加成 梁红梅 李慧敏
1(应用数学福建省高校重点实验室 福建 莆田 351100)2(莆田学院数学与金融学院 福建 莆田 351100)3(闽南师范大学数学与统计学院 福建 漳州 363000)
0 引 言
在传统的公钥密码系统中,用户的公钥是通过公钥基础设施PKI颁发证书来认证的,由此出现了公钥证书的管理、存储、发布、验证等问题[1]。为了简化证书的管理等问题,1984年,Shamir[2]首次提出了基于身份的公钥密码体制,在该体制中使用能够唯一识别该用户身份的公开信息来作为用户的公钥,这样用户的公钥就不再需要PKI颁发证书认证,从而降低了PKI的证书管理等问题的复杂性。但是,在基于身份的公钥密码体制中,用户的私钥完全由KGC产生,使得基于身份的公钥密码体制存在密钥托管这一新问题。为了解决该问题,Al-Riyami等[3]在2003年的亚洲密码学会议上首次引入了无证书公钥密码学概念,解决了基于身份公钥密码学中存在的用户密钥托管问题,也解决了PKI中存在的证书管理问题。
在无证书认证动态群组密钥协商协议中,对于动态群组中人员的变动后组密钥的更新总是困难的。伍前红等[4]提出针对基于ASGKA(Asymmetric Group Key Agreement)协议,允许成员的离开和加入,且高效地完成了密钥的及时更新。但是由于群成员可能来自不同的时区、领域、网络类型,而ASGKA不能满足该需求。张启坤等[5]提出基于身份的可认证非对称群群组密钥协商协议(Identity-Base authenticated Asymmetric Group Key Agreement,IB-AAGKA)解决了群成员因各种差异不能保持多轮在线密钥协商问题和实现匿名与可认证性并且支持节点的动态群组密钥更新的问题。由于是基于身份的公钥密码体制,存在密钥的托管问题,陈若昕等[6]提出无证书非对称群密钥协商协议,实现了对于群成员公开信息认证的同时又认证了其身份,保证了成员的安全通信,提高了效率。现今随着网络计算、即时通信、对等网络数据共享愈加重要,在这类通信中两方密钥协商协议显得非常重要[7-11]。但是,对于三方以上的秘密通信问题,学者们提出了组密钥协商协议[12-15]。最近,Kumar A和Tripathi S提出了一个无双线性对的匿名无证书动态群组密钥协商协议[13]。经过分析发现,该群组密钥协商协议是不安全的。本文指出了该协议存在的安全问题,并给出了具体的攻击方法,最后给出了应对该攻击的改进方法。
1 预备知识
1.1 双线性对运算及其性质
设G1为p阶加法循环群且P是它的一个生成元,G2为p阶乘法循环群,若映射e:G1×G1→G2满足下面三条性质,则称为双线性对运算。
(2) 非退化性:存在P∈G1,使得e(P,P)≠1G2,其中1G2表示群G2是单位元。
(3) 高效性:对于任意P,Q∈G,都存在有效的算法计算e(P,Q)。
1.2 困难性假设
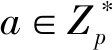


1.3 符号说明
表1为本文用到的一些符号。
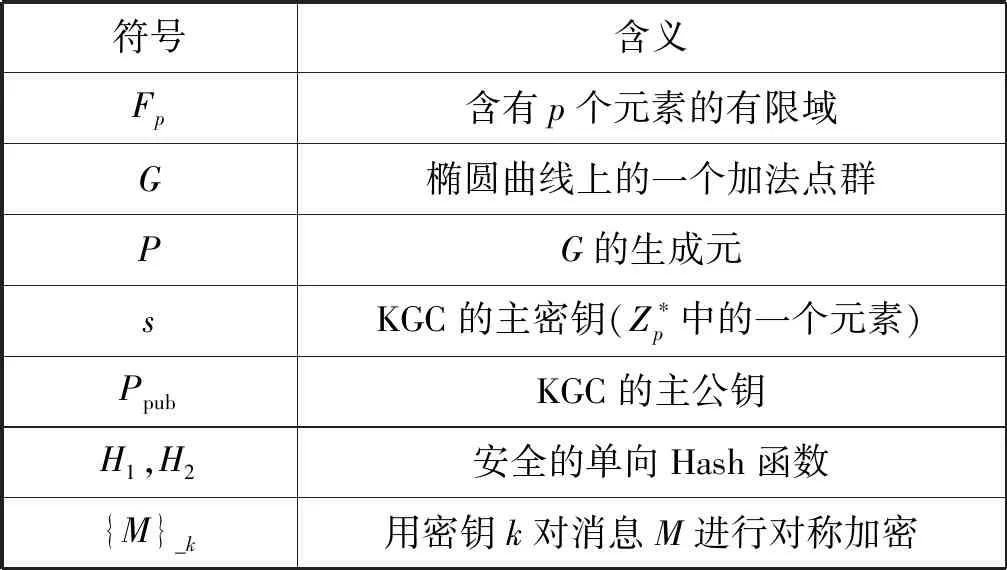
表1 符号说明表
2 组密钥协商协议
2.1 生成公钥与私钥
(1) KGC选择安全参数k∈Z+并执行以下操作:
① 选择一个k位素数p,并确定出{Fp,G,P}。
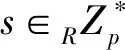
③ 对于安全参数k,KGC会选择两个安全Hash函数作为秘密值:
H2:G×G→{0,1}k
④ KGC发布{Fp,G,P,Ppub,H1,H2}作为系统参数,然后秘密保存主私钥s。
(2) KGC为用户颁布部分私钥Di,具体算法如下:
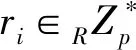
Ri=riP,hi=H1(IDi‖Ri‖Qi)
Si=(ri+shi)modp
KGC通过安全的信道向用户Ui颁发用户的部分私钥Di=
在收到KGC的部分私钥Di后,用户Ui可以通过下列的等式来验证:
Ri+Hi(IDi‖Ri‖Qi)Ppub=SiP
如果等式成立则部分私钥有效,反之无效。

(4) 用户IDi将SKi=
(5) 设置公钥,计算Pi=(xi+Si)P,Qi=xiP,用户IDi的公钥为PKi=
2.2 成员匿名身份的注册
(1) 每个用户按照下列步骤执行:
① 用户选择一个临时身份TIDi。
③ 用户Ui向KGC发送以下信息:
(2) 在接收到来自每个用户Ui的上述消息时,KGC执行以下操作:
① 计算Ki=sTi=(Kix,Kiy),1≤i≤n。
② 使用Kix对来自Ui的消息进行解密得到Ti的值。
③ KGC验证解密的Ti是否与从Ui接收到的Ti相同;如果验证成功,则执行后面的操作,否则拒绝。
④ KGC计算hti=H1(TIDi),Sti=(ri+shti)modp,1≤i≤n。
⑤ KGC向每个使用Kix加密的用户发送以下内容:
{Sti‖ht1‖Q1‖ht2‖Q2‖…‖htn‖Qn}_kix
2.3 密钥的协商
(1)Ui首先解密从KGC收到的消息并获得它们的临时部分密钥Sti,TIDj的哈希值和其他成员的公开密钥Qj(1≤j≤n),Ui也可以在列表中找到自己的位置,并根据列表中的位置设置下标。

(3)Ui将
①Ki,i+1=(xi+Sti)Wi+1+wi(Qi+1+Ri+1+ht(i+1)Ppub);
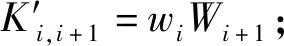
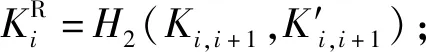
④Ki,i-1=(xi+Sti)Wi-1+wi(Qi-1+Ri-1+ht(i-1)Ppub);

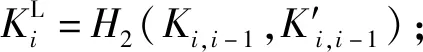
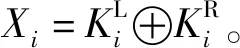
接着每个用户都将它们的Xi传播给群组中的其他用户,在得到所有Xj(j≠i)之后,Ui首先验证收到的消息如下:X1⊕X2⊕…⊕Xn=0。

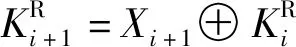
最后每个用户的组会话密钥计算为:
2.4 成员的加入
假设新用户{Un+1,Un+2,…,Um}想要加入现有的组{U1,U2,…,Un},则步骤如下:
(1) 从{U1,U2,…,Un}选择出两个用户U1和Un,重新选择秘密值x1和xn,更新它们的公私钥。此时的分组情况为{U1,U2,…,Un}与{U1,Un+1,Un+2,…,Um,Un}。
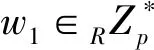
(3) 重复密钥协商阶段后与第一组{U1,U2,…,Un}得出密钥SK1与第二组{U1,Un+1,Un+2,…,Um,Un}得出密钥SK2。
(4)U1和Un把密钥SK1发送给第二组的其余成员{Un+1,Un+2,…,Um},把SK2发送给第一组的其他成员{U2,…,Un-1}。
(5) 把两组合并为{U1,U2,…,Un,Un+1,Un+2,…,Um},此时新的组密钥为SKnew=H1(SK1‖SK2)。
2.5 群成员的离开
假设U={U1,U2,…,Un}是当前组,并且L={Ul1,Ul2,…,Uln}是离开成员的集合,其中{l1,l2,…,ln}∈{1,2,…,n},此时我们将剩下的成员集合表示为:
A={Ua1,Ua2,…,Ua(n-n′)}=U-Ln>n′
令Ua1∈A作为离开管理员,用Ua1的临时身份将所有离开成员L的hti传播给A。该操作步骤如下:
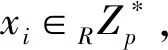
(2) 若成员Uk∈A,且其相邻的成员没有改变,就什么都不做,只是简单地传播它们之前已计算好的Xk作为新的Xnewk即(Xnewk=Xk),然后再传播给A。
(3) 每个成员Ui∈A在接收到所有的Xnewj(j≠i)后验证:
Xnewa1⊕Xnewa2⊕…⊕Xnewa(n-n′)=0
3 组密钥协商协议的安全性分析
本节对文献[13]中的密钥协商协议进行分析,指出攻击者无须知道用户的私钥即可以绕过KGC的身份验证,从而假冒用户参与组密钥的协商,盗取组密钥。
3.1 伪装用户
式中:Ppub为群成员Ui的公钥。
(3) 攻击者向KGC发送以下信息:
3.2 进行验证
在接收到来自攻击者的上述消息时,KGC会执行以下操作:
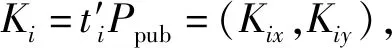
(2) 使用Kix对来自Ui的消息进行解密得到Ti的值,所以得到的Kix可以成功地解密得到{Ti,TIDi,Qi}。
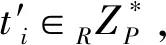
(4) 现在KGC计算如下:
hti=H1(TIDi)
Sti=(ri+s.hti)modp1≤i≤n
(5) KGC向每个使用Kix加密的用户发送以下内容:{Sti‖ht1‖Q1‖ht2‖Q2‖…‖htn‖Qn}_kix。

3.3 盗取密钥
(1) 在验证成功之后攻击者计算如下:
①Ki,i+1=(xi+Sti)Wi+1+wi(Qi+1+Ri+1+ht(i+1)Ppub);
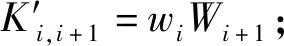
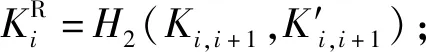
④Ki,i-1=(xi+Sti)Wi-1+wi(Qi-1+Ri-1+ht(i-1)Ppub);
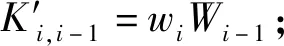
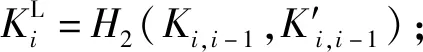
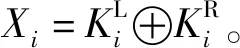
(2) 由于每个用户也会把它们的Xi传播给群组中的其他用户,则攻击者可以得到所有Xi,接收到消息之后,验证等式是否成立:X1⊕X2⊕…⊕Xn=0。
在成功验证后,攻击者就可以通过上述数据计算:
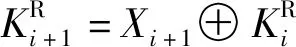
通过上述分析可知,攻击者可以成功绕过KGC的验证,从而伪装某个用户潜入进行组密钥的协商。因此,文献[13]中的组密钥协商协议是不安全的。
4 组密钥协商协议的改进
上述攻击成功的原因是KGC在用户匿名身份的注册中无法证实用户的真实身份。针对这个问题,下面给出两种改进方法,使得KGC可以确信用户的真实身份。这里采用和文献[13]一样的系统参数。
4.1 改进方法一
(1) 让用户选择一个临时身份TIDi并且随机选择ti∈RZp*,计算如下:
Ti=tiP,Ki=tiPpub=(Kix,Kiy)
(2) 计算完成之后Ui向KGC发送以下信息:
(3) KGC接收到Ui信息后可计算Ki=sTi=(Kix,Kiy)得到Kix(因为tiPpub=tisP=sTi)。
(4) KGC根据Kix解密得到{Ti,TIDi,Qi,
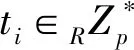
(6) KGC根据Kix解密得到的
显然,由于用户的部分私钥是KGC为其生成并且通过安全信道发送给用户的,即用户的部分私钥只有用户和KGC拥有。攻击者若想要替换用户的公钥,还需要生成和用户身份及新公钥一致的部分私钥,就必须从Ri=riP,hi=H1(IDi‖Ri‖Qi),Si=(ri+shi)modp中获得主私钥s才可以做到,这是求离散对数困难问题,所以该改进方法是可行的。
4.2 改进方法二
改进方法一是把用于用户的部分私钥直接作为被加密的内容进行传送,虽然是用加密的方式传输,但若在数据的解密过程中使用不当,容易导致用户私钥的泄露。所以这里采用数字签名的方法加以改进,具体如下:

(1)Ti=tiP;
(2)Ki=tiPpub=(Kix,Kiy);
(3) 令v=H1(IDi‖Ri‖Qi‖Ti),计算u=ti+Siv;
(4) 发送
(5) KGC验证uP=Ti+vRi+vhiPpub,式中hi=H1(IDi‖Ri‖Qi)。
验证正确性:
uP=(ti+Siv)P=tiP+SivP=Ti+(ri+shi)vP=
Ti+rivP+shivP=Ti+vRi+vhiPpub
由此可知,(u,Ti)事实上为用户使用部分私钥Si对身份和公钥消息IDi、Ri、Qi做的数字签名。如果攻击者想要冒充群组里的成员,就必须得到用户的部分私钥Si,而用户的部分私钥只有用户和KGC拥有。或者攻击者得从Ri=riP、Ppub=sP中去计算得到ri和s,这显然也是离散对数问题,所以该改进方法是可行的。因此,通过这个方式KGC可以确信用户的真实身份。
5 结 语
本文对文献[13]中的组密钥的协商进行了分析,指出该协议是不安全的,给出具体的攻击方法,并在此基础上提出了应对该攻击的两种改进方法。第一种是在发送给KGC的内容中直接添加用户的部分私钥去让KGC验证;第二种是使用用户的部分私钥进行签名后再发送。本文给出的分析方法对于同类协议,特别是基于无证书公钥系统的协议的设计具有借鉴意义。
