开孔十字型屈曲约束支撑的有限元分析

高 雅，李晨阳

(兰州交通大学 土木工程学院，甘肃 兰州 730070)

从古到今，地震带给人类的危害不可预估，其强大的破坏力严重地威胁着人类的生命和财产安全，为了能更好的降低地震危害，如何改善结构稳定性已成为如今研究的主要热点之一。屈曲约束支撑作为一种新型的耗能减震构件，其在工程中的应用极为广泛，经济效益也是非常突出的，但大部分屈曲约束支撑在地震发生时端部容易失稳破坏的现象严重阻碍了其在工程结构中的发展[1]。

针对屈曲约束支撑端部容易失稳破坏，核心部位屈服点难以确定的问题，国内学者进行了大量的研究与创新，邓雪松，邹征敏[2]等人在2010年提出了开槽三重钢管防屈曲支撑形式，并对其进行试验研究与有限元模拟；2012年周云[3]等人又提出了开孔与开槽式三重钢管防屈曲支撑的形式及设计方法；同年，唐荣[4]提出了新型板式防屈曲耗能支撑；2015年时邓雪松，纪宏恩[5]等对板式开孔防屈曲支撑进行了滞回性能分析；2017年李丽平[6]提出一种新型开孔式一字形防屈曲支撑，并对其进行了理论分析和抗震性能研究，取得一定成果。

本文结合相关规范，提出一种开孔十字型屈曲约束支撑，并利用有限元软件ABAQUS对普通十字型支撑，不开孔十字型屈曲约束支撑，单排开孔十字型屈曲约束支撑，双排开口十字型屈曲约束支撑进行了仿真模拟，分析比较它们的力学性能差异，选出最优构件，为后续的相关研究提供理论基础。

1 屈曲约束支撑构造

屈曲约束支撑的横向是由内核单元、约束单元及滑动约束机制单元[8]三部分组成，如图1所示；它的纵向组成主要包括：屈服耗能段，过渡段和连接段，如图2所示。

屈曲约束支撑形式多种多样，但其原理都是大同小异的。如一字型截面、十字型截面、工字型截面等[9]，都是在轴向张力和压力的作用时，利用芯材屈服耗能的原理，再加上外部套筒对内部核心单元的约束，实现全截面屈服，减少屈曲失稳的发生，更好地耗散地震发生时产生的能量，减少或防止主体结构的损坏，从而提升结构的抗震性能[10]。

图1 屈曲约束支撑横向构成

图2 屈曲约束支撑纵向构成

2 屈曲约束支撑的设计方法

依据张浩飞[10]等提出的开孔十字型全钢防屈曲支撑抗震性能与设计方法研究，对内芯进行开孔段和非开孔段横截面积、承载力的理论设计。

2.1 开孔段和非开孔截面尺寸的确定

为了支撑能够满足设计承载力的要求，对已知的设计承载力P，依据《钢结构设计规范》[11]选取十字型内芯钢号，按公式1进行开孔截面的横截面尺寸计算。

式中：AC——十字型内芯开孔截面面积；

f——十字型内芯钢材强度设计值。

非开孔的截面尺寸用式2确定：

式中：A——十字型内芯非开孔段截面面积；

φ——十字型内芯截面开孔程度（%）。

2.2 承载力的确定

屈曲约束支撑涉及的承载力包括屈服承载力和极限承载力，屈服承载力主要用于结构的弹塑性分析，是支撑第一次进入屈服耗能时所受到的轴向力；极限承载力主要用于屈曲约束支撑的节点及连接设计，是应变强化后的最大承载力。其计算公式如下：

式中：A1——内核单元截面面积；

fy——内核单元所选钢材屈服强度；

υ——材料拉压不平衡影响因子，一般取1.1；

Ω——材料应变强化因子，一般取2.25。

2.3 内芯的设计

本文选择实体工程的某一区间进行计算，根据图3的结构布置形式，经计算得出构件的长度为4350mm，设计承载力为50t，设计出与之相适应的屈曲约束支撑构件，如图4所示。

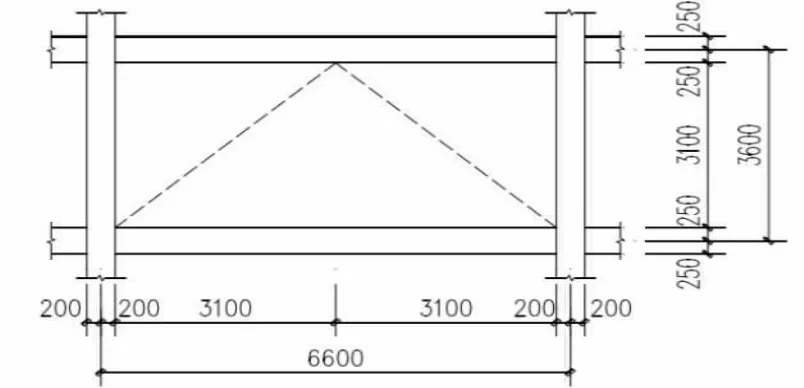
图3 支撑布置结构图

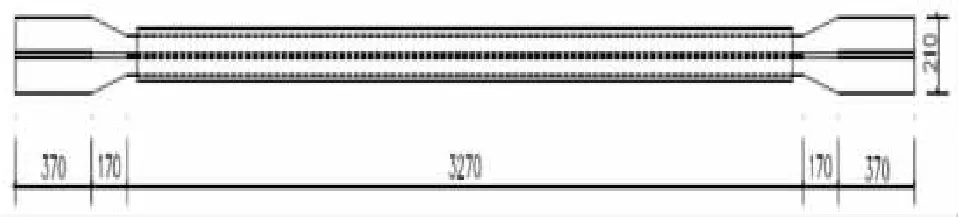
图4 构件整体尺寸图

3 有限元建模

3.1 构件设计

本次试验在第二节的基础上共设计了4组试件，试件编号及具体参数见表1，所有实验构件内芯均采用Q235钢，外套管除普通十字型支撑外，均采用Q345钢；构件中内芯具体开孔尺寸如图5所示，内芯横截面尺寸图如图6所示。

表1 支撑形式

图5 内芯开孔示意图

图6 内芯横截面尺寸图

具体开孔位置如图7所示，BK-3是在内芯的二等分点处开孔，为单排开孔（单排指的是从纵向看孔洞为一排）；BK-4是在内芯的三等分点处开孔，为双排开孔（双排是指从纵向看孔洞为两排）。

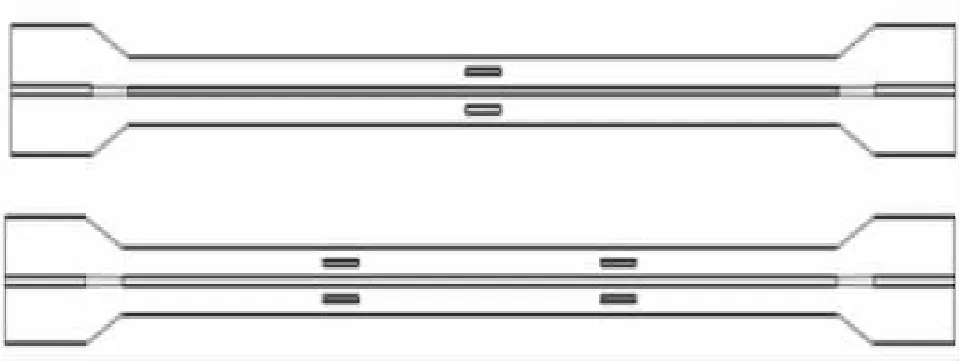
图7 BK-3、BK-4支撑开孔示意图

3.2 模型建立

在建立模型草图时，由于ABAQUS难以准确定位支撑的开孔位置，本文采用AutodeskCAD2016实现三维实体建模，模型建立如图8所示，保存为“*.sat”文件后导入ABAQUS6.14中进行分析，在ABAQUS中模型的部件类型为三维可变形，部件形状为实体。

图8 CAD中的屈曲约束支撑模型

3.3 材料属性定义

本文屈曲约束支撑采用的材料本构关系为弹-线性随动强化模型，如图9所示；十字型屈曲约束支撑的屈服耗能段和过渡段使用Q235钢材，弹性模量为Es=2.06×105Mpa，泊松比μ为0.3，密度ρ=7.85×10-9ton/mm3，弹性阶段时 E=Es，在进入塑性阶段时，刚度为0.02E；连接段和外壳钢使用Q345钢材，弹性模量为 Es′=2.66×105Mpa，泊松比 μ 为 0.3。在ABAQUS中内芯屈服耗能段Q235钢弹塑性参数的设置见表2。

图9 应力-应变关系图表

表2 屈服耗能段Q235钢弹塑性参数表

3.4 相互接触定义

从图6中可以看出，为了让内芯与外套管更好地接触，内芯横截面的4个端部被设计成倒角，让其与套筒内壁面平行。本文的模型在ABAQUS中的相互作用定义为“表面与表面接触（standard）”[12]，此接触由主从面构成，选择内芯屈服耗能部分的倒角面为主表面，外壳的内壁面为次表面，滑移公式选“有限滑移”，接触跟踪为“单配置状态”；在创建相互作用属性时通常要考虑到切向和法向的作用，由于内芯部位一般都有涂抹无粘结材料，摩擦力可以忽略，所以切向行为为“无摩擦”，内芯和外围单元间接触面的法向行为为 “硬接触”，允许接触后分离。

3.5 创建约束以及边界条件

本次数值模拟采用的约束类型为“耦合的”，是在核心单元最左端截面处和穿过截面形心的一点设置“耦合约束”，这样在这一点处加载位移，可以得到更精确的分析结果，如图10所示；边界条件所选分析步的类型为“位移/转角”，其中左端除轴向位移外，约束剩余的自由度，即U1=U2=UR1=UR2=UR3=0，右端为完全固定，约束所有的位移和转角，即U1=U2=U3=UR1=UR2=UR3=0，套管是约束两端3个方向的位移，即U1=U2=U3=0。

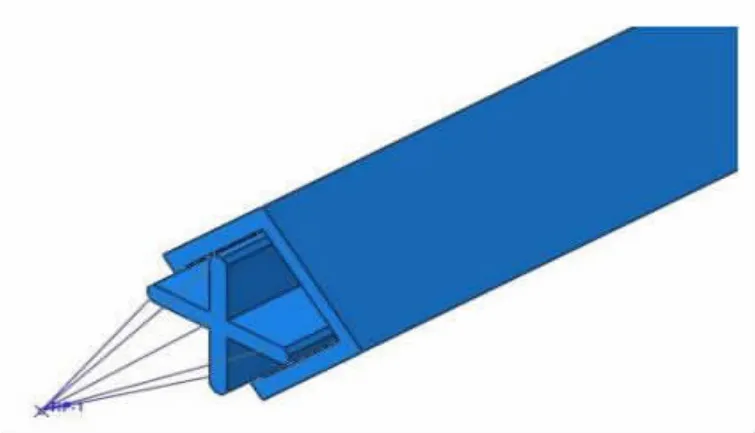
图10 耦合约束设置图

3.6 网格划分及单元类型的定义

在ABAQUS 6.14中进行模型分析时，构件采用全局布种模式，内芯屈服耗能段的近似全局尺寸限制在7.5mm，螺栓连接处的近似全局尺寸限制在12.5mm，最大偏离因子及最小尺寸占全局尺寸的比例采用默认值0.1，以下图BK-4的网格划分为例。

由于支撑构件在受到压力时，开孔处会发生大的变形，所以在分析时采用C3D8R单元[10]（八结点线性六面体单元, 减缩积分,沙漏控制），求解结构可以更精确一些。如图11、12所示。

图11 耗能屈服段网格图

图12 螺栓连接处网格图

3.7 加载制度

模型的加载分2种：一为单向加载，是在构件的端部施以压力荷载，分析它们的力学性能；二为低周反复加载系统，其使用位移控制的拟静态加载[13]，用来探讨每种支撑类型滞回性能的不同。各级位移加载振幅基于构件的屈服位移△by，以△by、2△by、4△by、8△by、12△by进行单周来回加载。

3.8 屈曲分析及初始缺陷引入

由于支撑构件在出厂时往往伴随着一定的缺陷，所以引入初始缺陷的模型分析会更精确一些。在ABAQUS中对四组支撑的内芯部分进行特征值屈曲分析时，首先取得支撑的高阶屈曲模态，看它的核心部位是否出现预测的高阶半波屈曲，而不是高阶扭转屈曲；其次由计算得到四组支撑内芯的各阶屈曲模态。由于奇数阶与偶数阶屈曲模态形式相似，本文以开孔数多的BK-4为例，选取前八阶的奇数阶进行分析，如13所示。

图13 奇数阶屈曲模态图

从图13中发现，奇数阶屈曲是沿Y轴进行的，支撑的核心部分在外壳的约束下，从第一阶的一个半波屈曲，在第七阶处出现了三个半波屈曲，没有出现扭转屈曲问题。由于一阶屈曲模式起主要作用，所以引入四组构件相应的内芯一阶屈曲模式为初始缺陷，其值为板厚的1%[4]，也就是0.13。

3.9 各组支撑的单向加载模拟

本次模拟使用位移控制对各组支撑进行单向加载，在3.5节中提及的“耦合点”处施加压位移，为了方便横向对比和图示，压位移最大值为20mm，用正值表示，得到的荷载-位移图如图14、15所示。

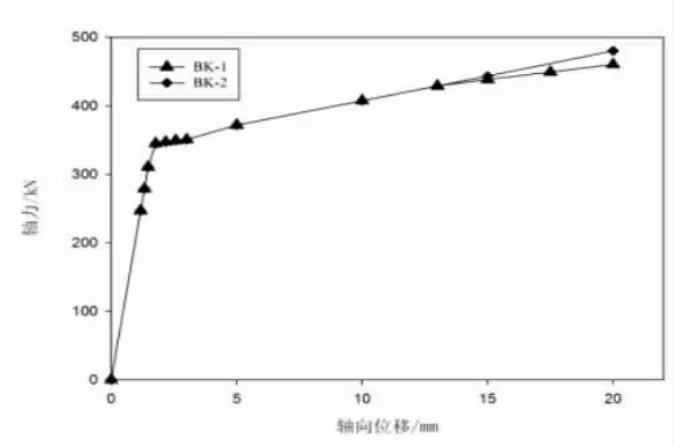
图14 BK-1与 BK-2荷载-位移图

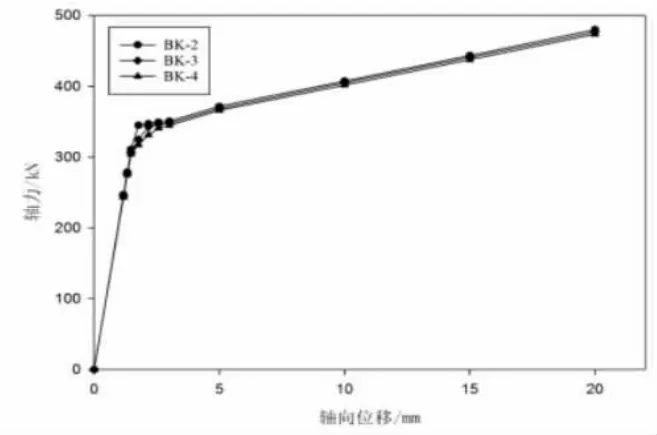
图15 BK-2、 BK-3、BK-4荷载-位移图

从图14中可以看出，当压位移为13mm或更小时，BK-1和BK-2力学性能相似；而在15mm后，因为初始缺陷的存在和压位移的增加，BK-1出现部分屈曲，刚度下降，BK-2由于外壳的约束刚度保持稳定；在20mm时，BK-2的承载能力为480.03kN，略高于BK-1的460.25kN。

从图15中可以看出，三者的屈服载荷并不相同。BK-2具有310.62kN的最高屈服载荷，BK-3的屈服载荷为 306.49kN，BK-4的屈服载荷为304.35kN。在压位移为3mm时，三个构件变化趋势相同；在压位移为20mm时，BK-2的承载力为480.03KN，BK-4的承载力为473.34KN，比BK-2低1.4%。表3为4组构件的承载力与屈服荷载对比。

表3 四组支撑单向加载结果统计表

3.10 各组支撑的滞回性能模拟

本节模拟了低周反复拉压载荷下四组支撑的滞回性能，构件荷载由位移控制，两端及外壳的边界条件采用3.5节中的设置，在单向加载模拟中，位移控制值与上节一致，载荷位移基准值采用与四组支撑相近的屈服位移△by=1.47mm。与单向加载不同的是，内核单元支撑需要同连接部分一起，在连接部分的左端选择加载位置。

图16 四组支撑滞回曲线图

从图17中可以看出，四组支撑构件在前四圈的加载中整体滞回曲线形式基本相似，而在第五圈加载时出现明显差异，BK-1开始出现较大的刚度退化和屈曲失稳，剩余三个屈曲约束支撑获得的滞回曲线是完整且对称的；BK-4和BK-2的曲线形式比较一致，只是在压位移变得更大时，BK-2的耗能相比BK-4来说要好；BK-4比BK-3的曲线相比，看起来要饱满一些，耗能要强些。

从图16可知，四组支撑的刚度在拉位移为13mm或者更大时均出现降低的趋势，而BK-3降低得更为严重；当压位移增加到-13mm后，BK-1因其本身的屈曲不稳定性导致刚度急速降低，承载能力也随之降低，其他三组支撑在压力作用下中都没有发生刚度降低的现象。

图17 四组支撑的骨架曲线

4 结束语

在本文中，利用有限元软件ABAQUS对普通十字型支撑、不开孔十字型防屈曲支撑、开单排孔十字型防屈曲支撑以及开双排孔十字型防屈曲支撑进行单向加载和低周反复加载的模拟结果进行比较分析，得出以下结论：

1）在单向加载的过程中，在压位移为大于10mm时，普通十字型支撑开始出现刚度退化，其承载力在塑性阶段就出现下降趋势，而屈曲约束支撑整个过程中均未出现刚度退化，力学性能优异；尤其是双排开孔十字型防屈曲支撑在压位移为20mm时，承载力仅比不开孔十字型防屈曲支撑低3.3%，具有良好的力学性能。

2）通过单向加载、滞回性能分析以及骨架曲线的对比，双排开孔十字型屈曲约束支撑的屈服荷载更低，在地震时比主体结构更早地屈服耗能，保护主体结构，尽管开口削弱，但是承载能力和滞后曲线比不开孔屈曲支撑只低5%，并且性能优良，最终选定双排开孔十字型防屈曲支撑BK-4为最优构件。