考虑非期望产出的我国沿海主要港口效率分析

2020-07-13武永贵

甘肃科技 2020年2期

武永贵,田芳

（兰州交通大学交通运输学院,甘肃兰州 730070）

近年来，我国经济发展进入新常态，21世纪海上丝绸之路是中国国家战略的重要组成部分，该战略有利于加强与周边及世界各国贸易往来，优化资源配置。港口是海上丝绸之路的桥头堡，也是进行国际贸易的枢纽。在此背景下，测度我国海上丝绸之路沿线主要港口效率，探究其改进和提高的途径，对我国推进海上发展战略，应对经济发展新常态具有重要意义。

国内外学者们关于港口效率的测度主要有参数法和非参数法两大类。参数法以随机前沿函数（SFA）为代表，崔俊浩等[1]利用SFA方法对 2001-2009年我国9家港口上市公司的运营效率进行测度，结果表明9家港口上市企业的运营效率呈下降趋势。艾亚钊等[2]运用SFA模型测度了珠三角6个集装箱港口效率，并分析了港口类型和港口经营人性质对效率的影响。Tongzon[3]应用SFA方法测算全球25个集装箱港口的所有制与港口效率之间的关系，结果显示私有制港口的效率较高。SFA方法的特点是其假设的生产函数受主观因素影响较大，可能会导致评价结果的不准确。

数据包络分析法（DEA）是主要的非参数方法，DEA方法无需假设生产函数的具体形式，也不需要主观赋予指标权重，具有较强的客观性，因此得到了广泛应用。李兰冰等[4]以DEA模型和Malmquist指数为工具，从静态和动态分别测算两岸三地主要沿海港口效率，并分析了港口全要素生产率变动原因，最后对港口竞争力进行科学评价。沈金生[5]和王爱虎等[6]运用三阶段DEA模型分别测算分析了环渤海地区和珠三角地区港口效率，并给出了提升港口效率的对策。鲁渤等[7]分别采用DEA-CCR、DEA-BCC和DEA超效率三种模型，对中韩两国31个集装箱码头的运营效率进行测度，研究表现中韩两国港口效率存在明显差异。宁凌等[8]首先用DEA模型测算了我国海上丝绸之路主要港口效率，然后利用Malmquist指数分析了引起港口效率变动的因素，最后采用聚类分析对港口分类。

文献[1-8]只考虑了港口运营过程中的“好”产出，未将非期望产出纳入考虑。近年来，生态和环保问题日益受到重视，不考虑非期望产出的港口效率测度逐渐不能适应现实需要，因此，一些学者开始将非期望产出纳入效率测度框架。刘勇等[9]利用考虑非期望产出的网络DEA模型，对我国集装箱前十大港口效率进行测算，并分析了三大区域的效率差异。李顺[10]考虑环境代价，运用考虑非期望产出的SBM模型对我国十大集装箱港口效率测度，并利用Tobit模型分析了外部因素对港口效率的影响。

以上的研究为港口效率测度奠定了理论基础，也取得了许多研究成果。笔者认为，仍存在以下几个方面可以进一步完善：（1）我国海上丝绸之路沿线港口运营效率和发展特征的文献较少；（2）多数文献采用单一的方法对港口效率进行测度，静态测算和动态测算相结合，且从港口效率和规模综合评价港口竞争力的文献较少；（3）多数文献只考虑“好”产出，考虑非期望产出的文献较少。基于上述分析，本文的研究思路是，以DEA模型为工具分别测算不同情形下海上丝绸之路我国沿海主要港口运营效率，进一步利用Malmquist指数分析港口动态效率，最后分析港口运营效率变化的原因。

1 研究方法选择

1.1 非期望产出的SBM模型

数据包络分析（DEA）是一种静态效率评价工具，适用于多投入-多产出系统的效率分析，在既有研究中被广泛应用的DEA模型主要有CCR模型和BCC模型。这两类模型一般都从径向和角度出发进行效率测度，忽视了投入变量松弛问题和非期望产出问题。为了解决效率测度中的非期望产出问题，国内外学者提出的方法主要有距离函数法、投入产出置换法、正向转换法，但是这些方法都没能很好解决变量松弛和评价结果准确性问题。Tone等[11]提出了一种DEA改进模型：SBM模型，SBM是一种考虑松弛变量的非径向、非角度的效率测度方法，此外还能考虑非期望产出问题，提高了效率测度的准确性。

SBM模型中，假设有个决策单元（DMU），每一个DMU对应的投入变量有m种，记作X；期望产出变量有s1种，记作Y8；非期望产出变量有s2种，记作Yb;则，和。根据定义矩阵X、Y8和Yb分别表示为：

考虑非期望产出的SBM模型数学表示如下：

式中：P*表示决策单元的效率值，且；分别表示投入、期望产出和非期望产出的松弛变量；w为权重向量；当P*=1时，的值均为0，决策单元达到效率最优，P*<1时，未达到有效前沿，决策单元无效。如果在（1）和（2）组成模型中加入约束条件 Ew=1，则可以转化为规模可变条件下的SBM模型。考虑到（1）和（2）组成的模型为非线性规划模型，可以利用Charnes-Cooper转换方法将其转化为如下形式的线性规划模型求解：

1.2 Malmquist指数

Malmquist指数是在DEA效率分析法的基础上发展而来的一种测算全要素生产率（Total factor productivity,Tfp）的方法，可测度决策单元不同时期全要素生产率变动情况。本文运用Malmquist指数对港口效率进行动态分析，该指数是以投入距离函数来计算产出效率，基于投入的t期和t+1期的Malmquist指数分别可以表示为：

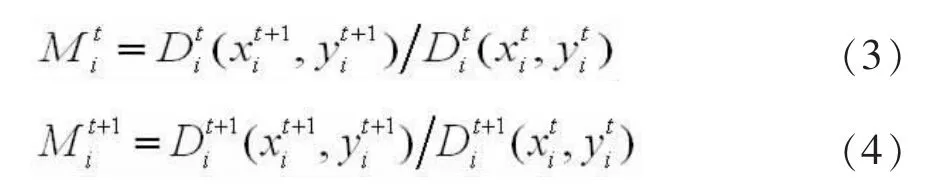
根据公式（5），Malmquist 指数可以分解为技术效率变化(Effch)和技术进步变化(Techch)。对公式（5）进一步变形，技术效率变化又可以进一步分解为纯技术效率变化(Pech)和规模效率变化(Sech)，因此，Malmquist指数可以表示如下：

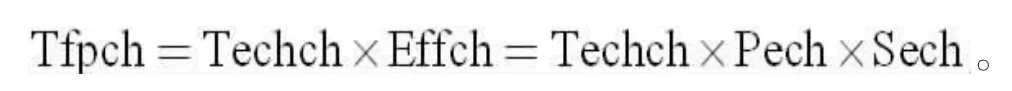
通过分析，可以找到技术效率变化和技术进步变化对全要素生产率的影响，从而找出生产率增长或下降的根源，为生产实践提供指导。

2 指标确定及数据来源

“一带一路”建设愿景与行动中明确提出要重点建设海上丝绸之路沿线城市港口，包含上海、宁波-舟山、厦门等15个港口。从历年的统计数据来看，该15个港口货物吞吐量占全国主要港口货物吞吐量的80%以上，能够较完整的反映我国港口行业情况。考虑到数据的可得性，最终选择如表1的14个港口（泉州港数据不可得）作为海上丝绸之路范围我国沿海主要港口的代表（以下简称沿海主要港口）。

表1 海上丝路我国沿海主要代表港口

基于上述分析，本文选取2008年至2017年表1中14个港口的统计数据为研究样本，选取决策单元数为14，时期数为10。指标数据均为客观数据，整理于《中国统计年鉴》和《中国港口年鉴》。参考既有文献[12]，并考虑指标的科学性及要能相对准确的反映港口运行情况，选取生产用码头长度、生产用泊位数、泊位长度和万吨以上泊位数为投入变量；港口货物吞吐量和集装箱吞吐量作为期望产出变量；既有研究中，很少有文献考虑非期望产出，为了更符合现实情况本文非期望产出变量选取港口碳排放量，具体计算方法参考文献[13]，研究样本数据描述性数据见表2。

表2 样本数据描述性统计

3 实证结果及分析

选择沿海14个主要港口为研究样本，运用以上方法，从不同角度来对上述港口运营效率进行研究。本文利用DEAP2.1和DEA-SolverPro5.0处理数据。

3.1 港口效率评价及分析

1）不同情形下沿海港口运营效率测度分析。根据整理的统计数据，利用DEA-Solver Pro5.0对沿海主要港口2010-2017年运营效率进行测算，分别计算得到考虑碳排放的和不考虑碳排放两种情形下沿海主要港口运营效率，结果如图1所示，数据见表3。情形一利用传统的CCR模型计算不考虑碳排放的港口运营效率；情形二计算的是将碳排放纳入考虑的港口运营效率。

表3 不同情形下港口运营效率比较

表3表明，在未考虑碳排放约束时，2008-2017年海上丝绸之路我国沿海主要港口运营效率均值为0.731，而在考虑非期望产出的情形二下，港口运营效率均值为0.689，这表明，在不考虑非期望产出时，港口运营效率被高估。二氧化碳等污染物排放是有环境成本的，它的排放抑制了港口效率的提高，因此考虑碳排放更加符合现实情况。从图1中可以看出，沿海主要港口运营效率2008-2017年间在波动中稳步提升，考虑碳排放约束下，港口运营效率从2008年的0.643提升到2017年的0.758，两种情形下港口运营效率变化趋势基本一致。

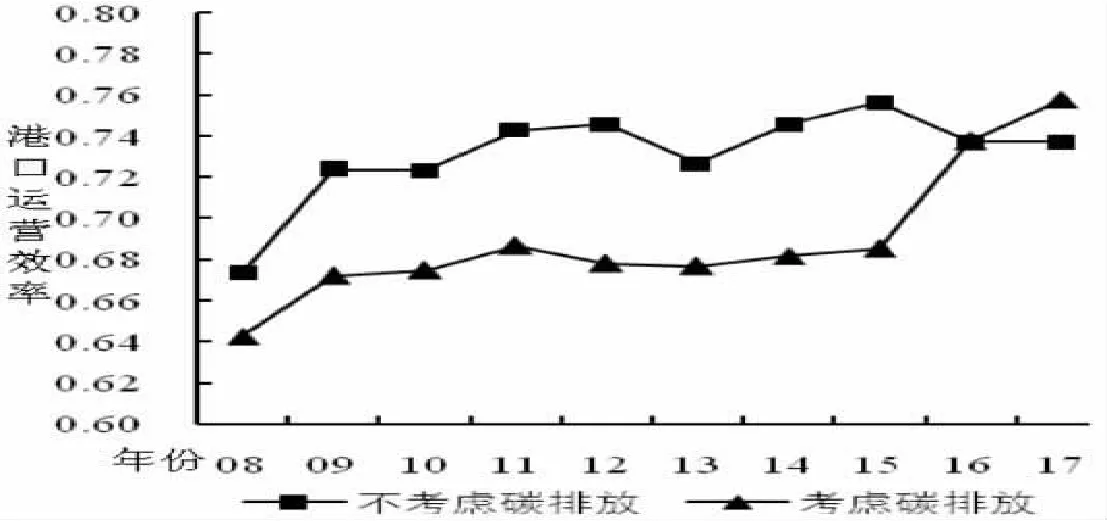
图1 不同情形下港口运营效率

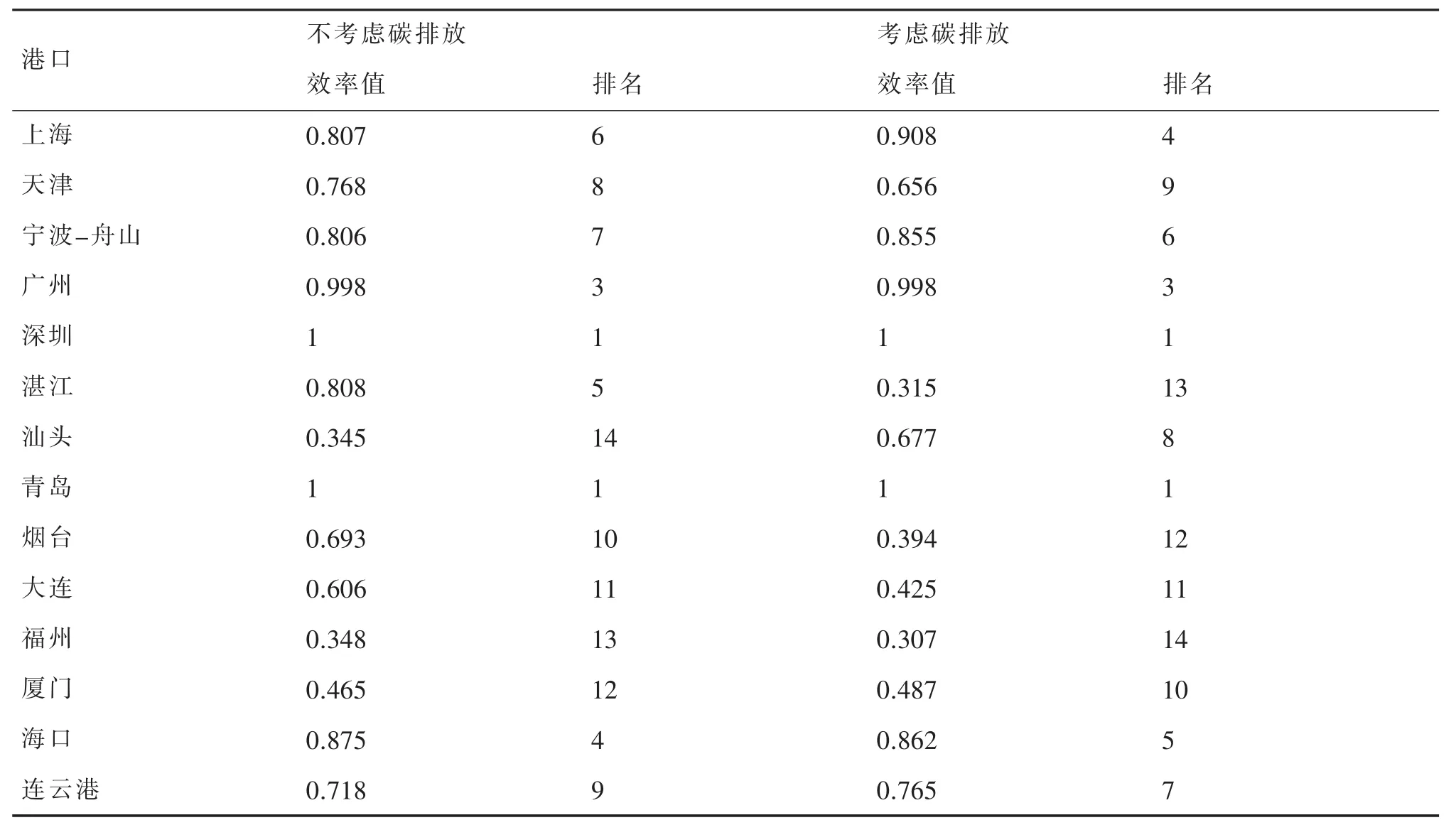
表4 两种情形下各港口运营效率比较

表4是两种情形下，沿海主要港口运营效率及排名对比分析情况。从表4中可以看出，2008-2017年沿海各港口效率差异显著。从排名变化情况可以发现，在考虑非期望产出时，上海、宁波-舟山、厦门、汕头等经济较发达地区港口排名有所提升，相反湛江、福州、海口等经济发展相对较弱地区的港口排名有所降低，表现出一种“强者恒强”的趋势，即经济越发达地区的港口，运营效率越高。呼应图1的情况，多数港口的运营效率在考虑非期望产出时会有所下降，这也说明只考虑“好”产出而忽视“坏”产出的港口运营效率测度是有待改进的。

2）分区域港口运营效率。按照港口所在的地理位置划分，本文研究的港口可划分为四大区域，见表1。分区域考虑碳排放约束下海上丝绸之路我国沿海主要港口2008-2017年运营效率见表5。

表5 分区域港口效率值

从表5可以看出，2008-2017年间沿海主要港口运营效率呈现出显著的区域不平衡特征。首先，长三角地区港口运营效率最高，均值为0.843，这与长三角地区经济总量与发展活力相关，该地区是我国经济最发达的地区，经济总量占全国的五分之一以上。珠三角地区港口运营效率次之，其值为0.794，该地区近年来发展迅猛，拥有广州、深圳两个一线城市，且毗邻香港，这些使得港口运营效率保持在较高水平。环渤海地区港口运营效率位居第三，与长三角和珠三角地区有明显差距。运营效率最低的是东南沿海港口，2008年受金融危机影响，该地区港口运营效率仅为0.343，而后止跌回升，但该地区以外向型经济为主，受累于世界经济状况进步比较缓慢。

3）吞吐量-效率矩阵构建与分析。衡量港口竞争力，一般是选取港口吞吐量对港口进行排名比较。然而，从港口运营效率的角度分析，该种方法只考虑了产出，而忽视了投入，不能科学的对港口竞争力进行评价。港口吞吐量大，不代表港口的运营效率高和竞争力强，例如，2017年宁波-舟山港吞吐量排名第一，而运营效率却位于第六位。因此，为了更加科学的评估一个港口的竞争力，选取2015数据，以港口吞吐量、运营效率值为横纵坐标，取港口吞吐量均值（35996.14）和运营效率均值（0.685）为分界，构建港口货物吞吐量-运营效率矩阵，结果如图2所示。根据图2，可以将港口划分为4种类型。

图2 港口货物吞吐量-运营效率矩阵

第一类是精干型港口，主要包括海口港、深圳港、连云港和汕头港，该类港口的特征是货物吞吐量不大，但运营效率较高，该类港口投入要素比较合理，有较大的发展潜力。

第二类是强壮型港口，包括上海港、宁波-舟山港、广州港和青岛港，此类港口不仅吞吐量大，而且运营效率高，这些港口腹地经济发达、集疏运系统完善，实力位居世界前列，具有较强竞争力。

第三类是瘦弱型港口，该类港口特征是吞吐量小，且运营效率较低，如烟台港、福州港、湛江港和厦门港。这类港口通常投入冗余、腹地经济不够发达，需要从投入和产出两方面调整，以提高运营效率。

第四类是肥胖型港口，指那些吞吐量很大，但运营效率却不高的港口，如大连港和天津港。该类港口通常有发达的经济腹地，但是对港口基础设施和先进技术等利用不充分，走向强壮型港口的关键是提高港口管理能力和效率。

3.2 Malmquist指数测算及分析

传统的CCR模型和考虑非期望的SBM模型效率测度属于静态效率评价，它只反映研究对象在研究期间的投入产出转化效率高低。为了进一步探究港口运营效率随时间变动情况和其影响因素，本文以Malmquist指数为工具对沿海主要港口全要素生产率作更深入的分析。

1）沿海主要港口Malmquist指数演化分析。根据Malmquist指数模型和近10年的统计数据，利用DEAP2.1计算得到2008-2017年沿海主要港口年均Malmquist指数及其分解，见表6，其变动趋势如图3所示。

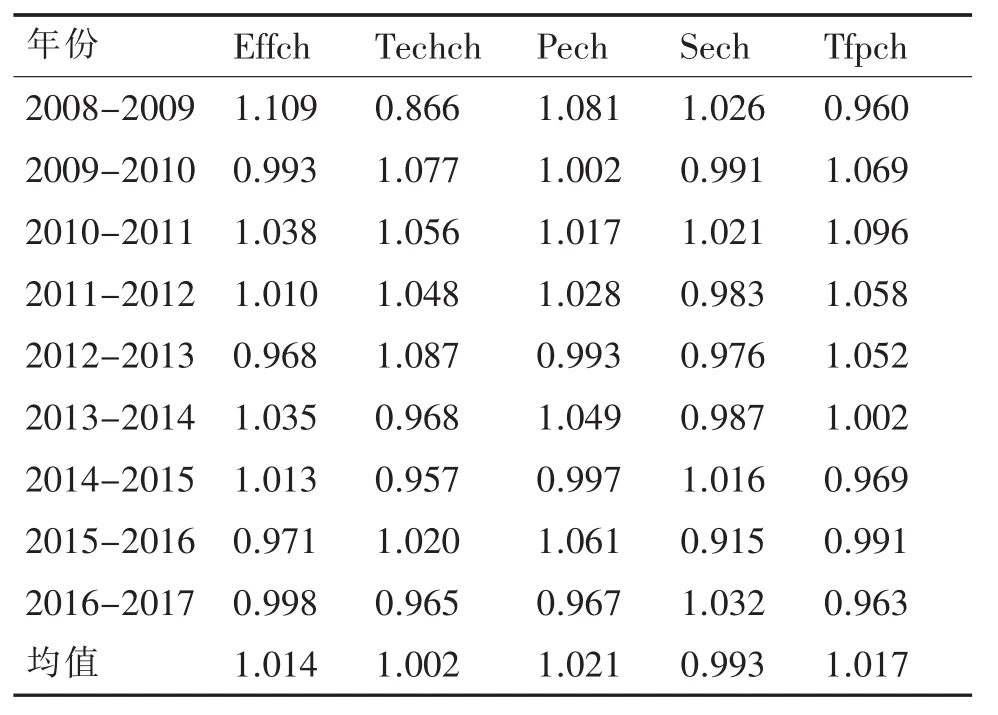
表6 港口运营效率分年度Malmquist指数及其分解

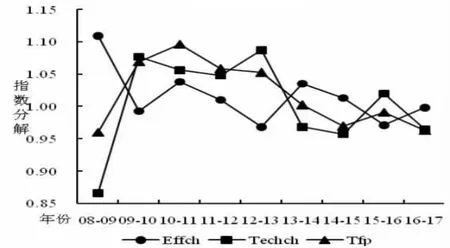
图3 沿海主要港口分年度Malmquist指数及其分解

表6表明，2008-2017年，沿海主要港口全要素生产率在波动中有所增长，其均值为1.017,说明港口生产率平均增长了1.7%。分年度分析，2008-2009年和2014-2017年港口全要素生产率出现了下降，而该时期恰好对应着国际金融危机和我国经济发展进入新常态及经济结构转型时期，比较符合实际情况的；2009-2014年间港口全要素生产率呈增长态势。

从表6和图3全要素生产率分解来看，2008-2017年港口全要素生产率的增长是技术效率和技术进步共同推动的结果，进一步分析发现技术效率对全要素生产率增长的贡献更大。然而，需要关注的是，在研究期间规模效率出现了下降，平均下降幅度为0.7%。

2）分港口全要素生产率演化分析。根据Malmquist指数模型，计算得到2008-2017年沿海各港口年均Malmquist指数及其分解，结果见表7。

从表7可以看出，2008-2017年沿海各港口全要素生产率差异显著，多数港口出现增长，其余港口出现小幅下降。除了海口港、连云港和青岛港外，其余各港口全要素生产率均出现了增长，其中湛江港增幅最大达到了8.6%，天津港增幅最小为0.3%。在全要素生产率下降的港口中，导致下降的原因有所不同，青岛港和连云港归咎于技术进步，然而海口港是技术效率和技术进步共同导致了下降。

表7 分港口年均Malmquist指数及其分解

3）分区域Malmquist指数演化分析。每个区域经济结构和管理体制等都会有所差异，因此有必要计算分区域的港口全要素生产率变动情况，其结果见表 8。

从表8来看，各地区各项效率变化有所差异。从全要素生产率分析：四大地区均实现了不同程度增长，其中东南沿海地区港口增幅最大，珠三角地区港口次之，环渤海地区港口最低。技术效率变化方面，四大地区港口也均实现了增长，但差距不明显。从技术进步变化分析，珠三角地区港口和东南沿海港口实现了增长，增幅分别为0.8%和0.6%，长三角地区港口保持不变，环渤海地区港口出现了小幅下降。考察全要素生产率变化的原因，除环渤海地区港口外，其余三大区域港口运营全要素生产率的增长是技术效率和技术进步共同推动的结果，然而环渤海地区港口全要素生产率增长则是由技术效率推动的。

表8 分区域港口Malmquist指数及其分解

3.3 港口效率的收敛性分析

收敛性分析是研究不同港口效率差异随时间变化的趋势，常用的有收敛分析。收敛是分析不同港口运营效率的离差随时间推移的变化情况，通常用变异系数来衡量[14]，其计算公式如下：

公式（6）中：cv是港口运营效率差异系数值；为沿海主要各港口运营效率；表示港口效率的算术平均值。cv值越大,表明各港口运营效率差距越大；如果cv随着时间推移，值逐步下降，则说明沿海主要港口运营效率存在收敛，计算结果如图4所示。

图4 沿海主要港口运营效率差异系数

图4分别显示了考虑碳排放和不考虑碳排放两种情形下计算的差异系数值。由图3可以看出，考虑碳排放情形下各年度差异系数均大于不考虑碳排放情形，这说明在考虑环境因素时，各港口运营效率差距在变大，有些港口已经向绿色港口发展转型，然而部分港口仍然以粗放式发展为主。从变化趋势来看，2008-2017年两种情形下差异系数值逐年变小，因此沿海主要港口运营效率存在收敛。