非线性广义系统传感器故障估计方法
2020-07-13孙延修王华颖路建波
孙延修,王华颖,路建波
(1.沈阳工学院 基础课部, 辽宁 抚顺 113122;2.河北经贸大学 数学与统计学院, 河北 石家庄 050061;3.国家卫生健康委科学技术研究所, 北京 100081)
0 引言
随着工业控制系统的复杂程度不断提高,人们对其可靠性的要求也日益引起重视,针对系统的故障诊断显得尤为重要。基于解析模型的方法早在20世纪70年代就已出现,近年来基于观测器的故障诊断方法陆续被提出。基于观测器的故障诊断与估计技术在理论研究中得到极大的关注并取得了一定的研究成果。目前,已形成多种鲁棒故障检测方法:滑模观测器方法[1-3]、未知输入观测器方法[4-6]、自适应观测器方法[7]等。针对系统故障诊断与重构,基于观测器特点的未知输入观测器方法和自适应观测器方法受到广泛关注。
广义系统是一种形式更加一般化而应用更加广泛的控制系统,它所描述的系统范围比正常系统广阔的多,其在电力、工程、经济、化学等领域有着广泛的应用。针对广义系统故障诊断与重构的研究受到越来越多的关注,伴随广义系统理论的发展,基于模型的故障诊断对这类动态系统的研究逐渐成为热点。近年来针对广义系统的研究,已经取得了一定的成果。文献[8]针对含输入干扰和输出噪声的广义系统的观测器进行了设计,通过观测器对系统中的执行器故障和传感器故障进行估计,但该方法针对系统中外部干扰与故障同时存在的情形并不适用。文献[9]针对系统含有外部干扰线性广义系统进行了研究,通过采用H∞技术对干扰进行最小化,利用设计的一种滑模观测器对故障进行重构,进而实现对故障故障的估计。文献[10]针对一类具有外部扰动的非线性广义系统的执行器故障提出一种重构算法,通过设计的自适应观测器实现了对故障的估计,并给出了估计误差一致最终有界的充分条件。文献[11]针对一类含执行器故障的非线性系统,提出一种新的故障诊断方法并对故障进行了估计,该方法需要假设系统无干扰且故障为缓慢变化故障。文献[12]针对含有干扰的非线性动态系统,通过构建自适应观测器同时对系统中的执行器及传感器故障进行了估计。文献[13]给出了基于滑模观测器的传感器故障检测与重构的方法,实现了系统传感器故障的检测和重构。文献[14]针对汽车稳定控制系统基于观测器对执行器与传感器进行了故障诊断与估计,但文章并未考虑干扰项。
基于上述分析,笔者针对同时含外部干扰和传感器故障的一类Lipschitz非线性广义系统传感器故障的重构问题进行研究。通过扩展系统状态向量,对状态进行重构并构造出增广状态观测器,考虑到系统中的干扰项,分别给出了观测器的误差动态方程渐近稳定的充分条件,进而实现对原系统中的传感器故障进行估计,在文献[12]基础上将含未知干扰的系统传感器故障估计问题推广到了广义形式,同时考虑到了观测器误差的收敛速度。
1 系统描述
考虑如下非线性广义系统:

(1)
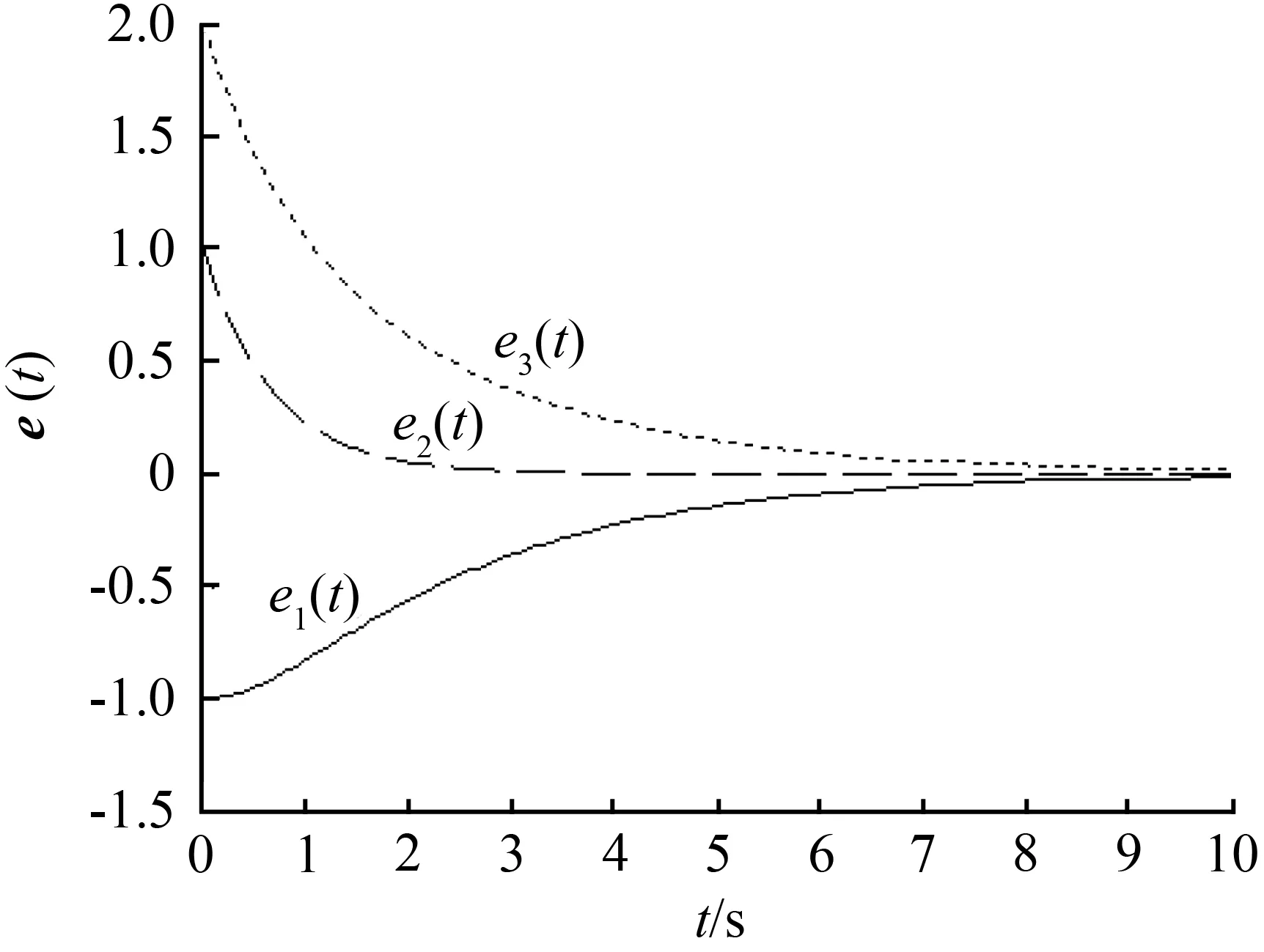
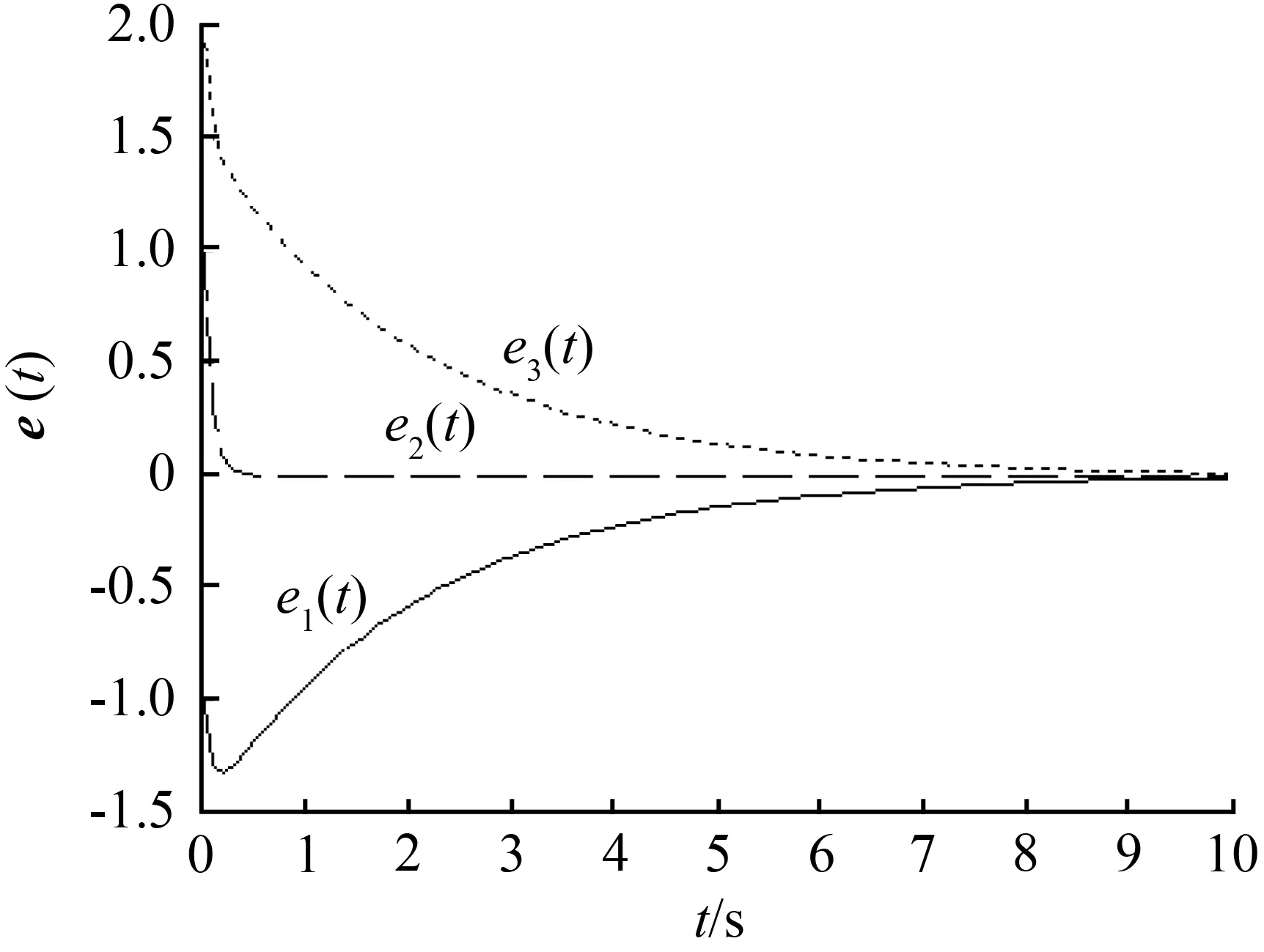
其中x(t)∈Rn为状态向量;u(t)∈Rm为控制输入向量;y(t)∈Rp为测量输出向量;d(t)∈Rl为系统干扰,f(t)∈Rq为传感器故障,E,A,B,C,D和F分别为具有适当维数的已知矩阵,其中rank(E) 假设2广义系统(1)中的非线性项Φ(x(t),t)满足Lipschiz条件: 文中所有‖·‖表示欧式范数,Lφ>0为利普西兹常数。 将传感器故障作为增广观测器中增广状态的一部分,通过构造增广观测器对原系统中的状态和传感器故障进行估计。 (2) 其中: 记, 式(2)可转换为: (3) 通过设计增广观测器可以实现对原广义系统中传感器故障的鲁棒估计,故可设计增广状态观测器如下: (4) (5) 可以通过Lyapunov函数证明观测器的误差动态方程为鲁棒渐近稳定,得到增广状态观测器的增益矩阵,从而实现对原系统状态和传感器故障的鲁棒估计。 定理1考虑系统(5),若存在正定矩阵P和增益矩阵L,满足如下线性矩阵不等式: (6) 证明取Lyapunov函数V=eTPe,则有: 2‖Pe‖‖ΔΦ‖≤2γ‖Pe‖‖e‖, 2γ‖Pe‖‖e‖≤γ(eTPPe+eTe), 即: 其中,γ=‖T‖Lφ。 所以, 其中: 当M1<0时,误差动态方程(5)渐近稳定,根据Schur补引理,M1<0等价于不等式(6),证毕。 定理2针对系统(5),若存在正定矩阵P、增益矩阵L和常数α,使得如下线性矩阵不等式: (7) ‖e‖<α‖d‖, 又, 故有, 参数α可以作为抑制干扰项d对传感器故障f影响的性能指标,当α变小时则表示干扰对故障的影响在减小,从而实现增广观测器对传感器的鲁棒估计。 ② 由于: 知, (8) 根据式(8)有: = 其中: 注2定理2考虑到了系统中的外部干扰,给出了增广状态观测器误差动态系统鲁棒渐近稳定的充分条件,同时通过矩阵不等式求解参数α使其最小,从而减弱了外部干扰对传感器故障估计的影响。利用MATLAB中的LMI工具箱求解线性矩阵不等式(7),可以求解出观测器的增益矩阵,从而实现对传感器故障的鲁棒估计。 例参考文献[15]中含传感器故障的非线性直流电机系统,设该系统广义形式的参数如下: 利用MATLAB可以计算出矩阵T,N分别为: 图1 不含扰动时观测器误差曲线 图2 含扰动时观测器误差曲线 本文针对同时含有外部干扰与传感器故障非线性广义系统的传感器估计问题进行了研究,提出了一种在传感器故障为常值突变或缓慢变化情形下,增广状态观测器的设计方法,并通过增广状态观测器对传感器故障进行鲁棒估计。当系统无干扰时,可以保证观测误差的收敛速度;当系统存在干扰时,可以减少外部扰动对传感器故障估计的影响。最后,通过仿真算例验证了观测误差渐近收敛,保证了增广观测器对传感器故障估计的有效性。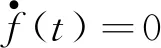

2 增广系统的设计
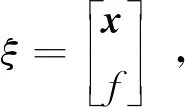


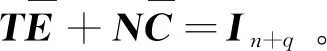
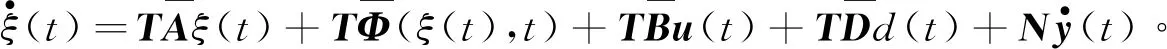

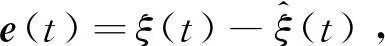

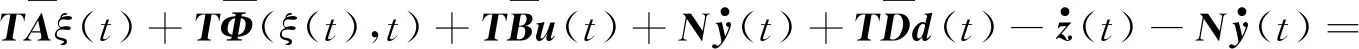
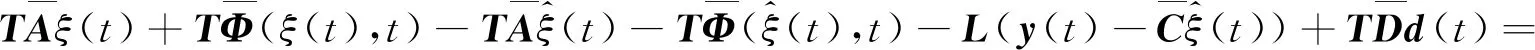
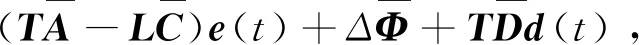

3 误差动态方程渐近稳定的充分条件
3.1 系统无干扰情形下误差动态方程稳定性证明
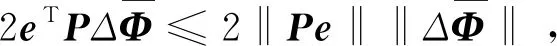

3.2 系统存在干扰情形下误差动态方程稳定性证明
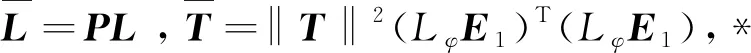



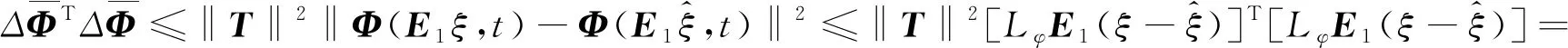

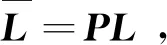

4 传感器故障估计
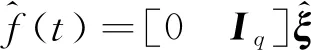
5 仿真算例
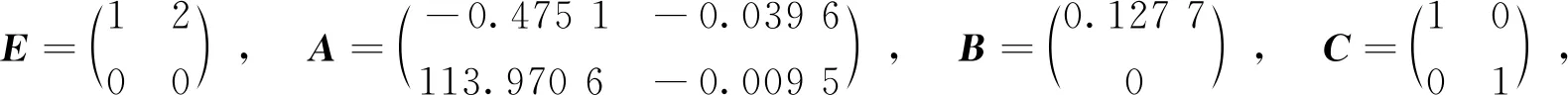
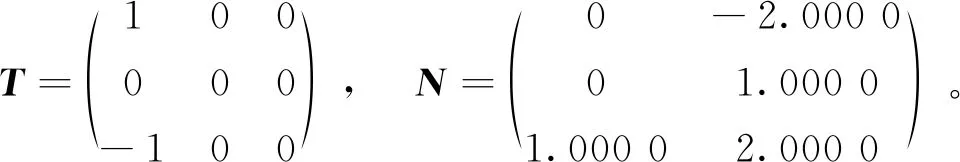



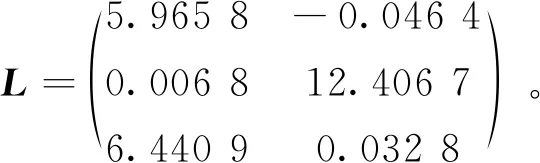
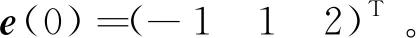
6 结语
