一种基于矢量变换的局部二值化模式分类方法

李安然，陈雪云

(广西大学 电气工程学院， 广西 南宁 530004)

0 引言

随着计算机视觉技术的发展，使用计算机视觉对数字图像目标进行识别和定位的准确性需求在不断提高。

对于常规的图像识别，通常是对识别图像进行特征提取后，增强或消除图像中的某些特征，再通过与目标图像特征的相似性和规律性进行对比，达到图像识别的效果。局部二值模式(local binary patterns，LBP)特征是常见的图像特征之一，它最初由OJALA等[1]提出，是一种有效非参数化的图像局部纹理描述方法。其基本原理是通过以某个像素为中心，对领域像素依次进行灰度值比较，如果周围像素灰度值大于中心像素灰度值，则该像素位置被标记为1，否则标记为0，按照固定方向即可串联得到一个八位的二进制值(转换成十进制后有256类)，按此方法遍历整张图像后，即可得到图像的LBP特征。一般来说，LBP方法能有效提取图像的纹理信息，保留像素空间位置关系，且具有旋转不变性和灰度不变性等显著的优点，被广泛应用于多种目标检测场景。在图像处理领域，LBP特征可以进行高效图像分割[2]；利用LBP特征可以进行USM图像锐化检验[3]和图像增强[4]；对于高光谱图像，LBP特征提取可以进行高光谱图像分类[5]。在生产安全领域，通过LBP特征可以识别森林火灾[6]；利用LBP特征提取可以进行柴油机失火故障分析[7]。通过对手掌纹理[8]、面部图像[9]进行LBP特征提取，可以得到较高的人脸识别精度。在医疗和认知学领域，刘晓虹等[10]提出了利用LBP特征进行肝脏CT图像识别；利用脑电纹理图像LBP特征，可以进行癫痫发作诊断[11]；在此基础上，LBP特征可以融合其他常见特征后进行中药饮片识别[12]。

为了优化LBP特征的维数及检测精度，后人在此基础上，通过对采样半径和采样点数进行控制，提出了圆形LBP类型，但圆形LBP特征的检测精度受到采样参数的影响，在选取合适的采样参数时耗费时间。文献[13]根据二进制值跳变次数对模式类型进行归类，提出了均值LBP特征，将原有的256类归为59类，减小了特征维数，但由于维数的过于缺少，导致检测精度不佳。近年，陈家华等[14]使用双线段采样的方法，提出了局部双线段模式(local lineal pattern, LLP)，扩大了采样邻域，取得了较高的目标检测精度，但双线段模式受到线段夹角影响，需要耗费时间调整参数，同时扩大的采样邻域,增加了处理器的计算负担。

针对上述缺陷，笔者提出了一种基于逻辑运算的局部二值化模式分类方法，该方法基于二进制值逻辑运算的思想，充分利用二进制值位数间的各个逻辑关系，对二进制值进行不同区域的逻辑运算，得到的逻辑组合值具有多种模式，丰富了LBP特征的模式层次，在减少特征维度的同时保证较高的检测精度。

1 局部二值模式(LBP)

LBP特征的主要思想是根据某像素点与周围像素点灰度值进行比较，以该点为圆心，生成一个半径为R的圆，在圆上按照等间距分布设有n个采样点，如果采样点的灰度大于中心像素点的灰度值，则该采样点的阈值标记为1，否则标记为0。按顺序串联所有采样点的阈值，得到一个局部二值化矢量V：

(1)

此时V即是LBP的矢量表达。这里设中心像素为(xc,yc)，ip表示采样圆上像素灰度值，ic为中心像素灰度值。sign()是一个符号函数：

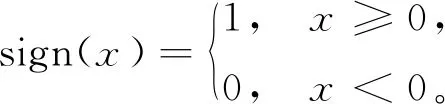
(2)

由中心像素(xc,yc)得到的二值矢量V的十进制LBP特征值为:

(3)

由式(3)可知，按照传统的八位LBP算法，一个中心像素可以产生256种不同的LBP值，在实际使用中，一张图片产生的LBP特征维度会很大。为了提高检测效率，文献[1]提出了均值模式LBP的概念，这实际上是一种占比归类的思想。在上述所有256类LBP值中，统计每个二进制代码从0到1或从1到0的跳变次数，例如00011110，跳变次数为2，10100000的跳变次数为3。当跳变次数小于等于2时，保持其值不变，即定义了一个均值LBP；跳变次数大于2的LBP值，不作为均值模式LBP，另外将其归为一类。经过统计，均值模式LBP在整个LBP特征中占了85 %～90 %，而均值模式LBP只有58个特征，所以均值模式LBP的特征向量把原有的256维降到了58维，提高了特征提取效率。在实际使用中，其实是有59维，加上了跳变次数大于2的另外一类。

针对特征采样区域固定，文献[1]提出了采样半径为变量R的圆形LBP特征,实现多尺度的LBP特征提取。与传统圆形采样相反，文献[14]提出的局部线段模式采用交叉线段结构进行LBP特征提取，通过调整线段夹角实现采样区域变换。

当对一张图片的尺寸进行调整时，如果采用原始的固定区域进行特征提取，提取结果将不一致。文献[1]对此做出了改进，采用圆形LBP的方法。圆形LBP顾名思义是将像素选取的形状从矩形变为圆形，采样范围从临近像素扩展到半径为R的圆形所在的采样像素位置。随着半径的增大或缩小，对周围的像素采样点数P也可以相应增减，以实现不同尺度的LBP特征的提取。

上述的LBP特征提取方法本质上都是基于对包围邻域的像素与中心像素对比求LBP值，而且大都用到了归类的思想来简化计算特征带来的高维数特征值。文献[14]提出局部线段模式(LLP)，即将原有包围邻域的方法改为局部线段的方法，使用两条相正交线段，以线段交点为中心，分别对每一条线段上任意个像素点按顺序进行采样，将两条线段的LBP值相互串联后就形成了LLP提取特征。采样时，两相交线段相对图片的夹角固定为90°，线段可以与图片有夹角，结果显示线段与图片的夹角在0°时具有最高的检测精度。考虑到均值LBP对局部特征提取能力强，但发散性弱的特点，与LLP特征的广域特点结合，后续该学者使用均值LBP的思想对LLP特征提取模式进行59类降维，即在原有的256类LLP值上进行0到58类归类，在一定程度上降低了特征的维数和计算量。

2 基于矢量变换的二值化矢量分类方法

本文提出的模式分类方法是建立在二值化矢量V的变换上，令γ代表V的变换函数，其自变量为二值化矢量V，输出为新的二值化矢量U。则定义局部二值矢量特征LVP(local binary vector pattern)定义为：

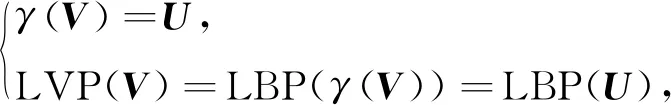
(4)

γ可以是任意变换函数，本文仅讨论基于局部块的变换函数,把二值化矢量V按照等间距，分割成顺序相邻的局部块，块长度允许长度为2，3，…。块分割方式包括不重叠和部分重叠两种，图1和图2给出了块分割方式示例。

(a) 块长度为2

(b) 块长度为3

图1 无重叠的块长度分割

Fig.1 Separation of non-overlapping block

允许块存在重叠的情况，如图2所示：

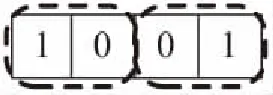
(a) 重叠百分比为0 %

(b) 重叠百分比为50 %

图2 不同重叠百分比的块分割

Fig.2 Separation in different percentage overlapping block

本文讨论的γ函数建立在对块的逻辑运算基础上，以块长度为2为例，基本的逻辑运算函数β包括与、或、与非和或非,具体见表1。

表1 块长度为2的基本逻辑运算β函数类表

γ函数可以写成：

γ(V)=γ(β(V))=[β(b1),…,bi,…β(bm)]=U,

(5)

这里bi是第i个块，i=1,…,m，假设V被分割成m个块。

β函数为fun1时，γ函数在采样点个数为8，块长度为2，不同重叠百分比时的变换结果见图3。

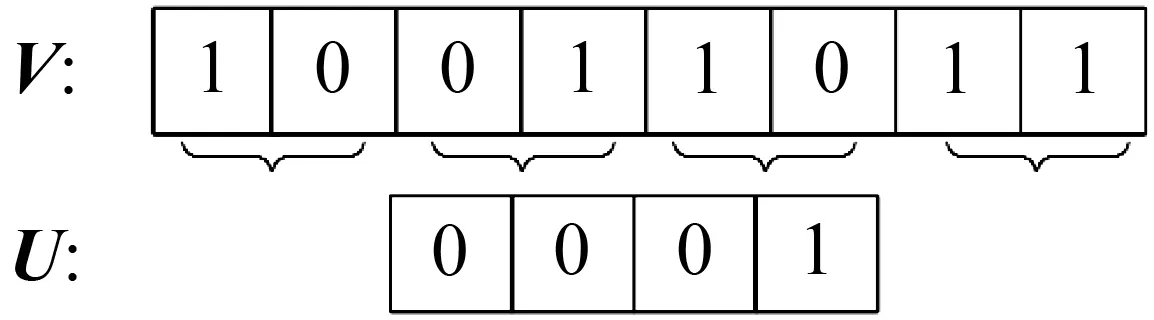
(a) β=fun1，块不重叠的矢量变换结果

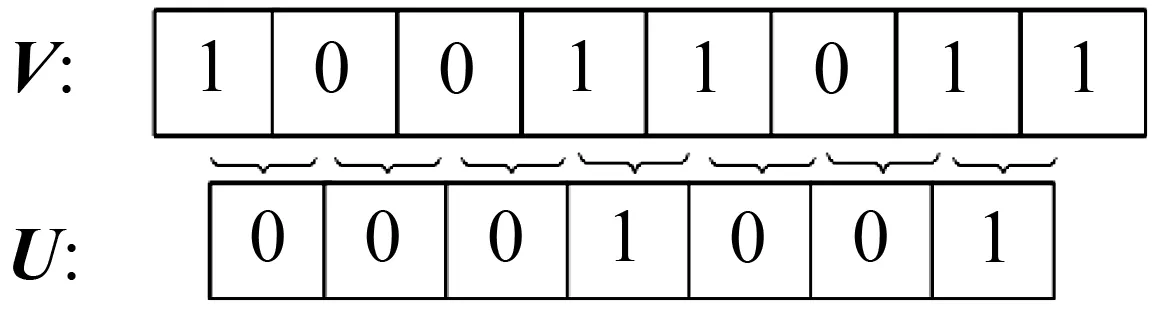
(b) β=fun1，块重叠50 %的矢量变换结果

显然，块的长度和块是否重叠对变换后输出矢量的长度有严重的影响。

为了解决根据块长度运算后输出矢量过小的问题，可以考虑将2个以上的基本逻辑函数输出值串接起来。

对应γ函数形式如下：

(6)

这里#=2表示fun1和fun2串接，以此类推。为了解决块长度为2重叠比为0 %时，输出矢量长度过小的问题，可以考虑将任意2个逻辑函数的四位输出二值矢量按照低四位和高四位的方法组成新的八位二值矢量，拼接如下：

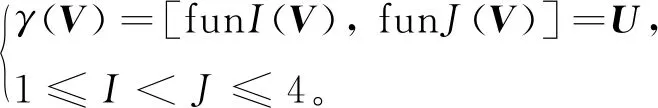
(7)

产生新八位二值矢量也可按照式(6)的逻辑函数输出值串接如下：

(8)

当块长度为2，重叠比为0 %时，以基本逻辑运算函数fun1和fun2为例的输出串接结果见图4。

图4 fun1和fun2串接，块长度为2，不重叠的矢量变换结果

3 实验过程与结果分析

3.1 数据库建立

为了研究本文算法的改进情况，增加说服力，笔者在研究LBP特征改进时，主要使用的数据库为公开的行人数据库INRIA，该行人数据库由7 000个含有行人的正样本和3 000个没有行人的负样本图像构成，均是从2 573张高分辨率图像中按照数据库给定的标定点裁剪后得到，裁剪后每个样本可用像素大小为64×128。为了测试改进特征的实际效果，增加说服力并说明普遍适用性，本文使用了文献[15]的遥感卫星数据库中的车辆和飞机两种遥感目标进行改进后特征的检测结果。其中，车辆数据库由4 000个车辆正样本图像和4 000个复杂环境下的非车辆负样本图像组成，飞机数据库由4 000个飞机正样本图像和4 000个复杂环境下的非飞机负样本图像组成。所有车辆、飞机样本数据均从100张高分辨率车辆遥感图像和100张高分辨率飞机遥感图像中标定切割而来, 每个样本大小均为48×48像素。部分行人、车辆、飞机数据库的正负样本如图5所示。

3.2 LBP逻辑运算处理

为了减少遍历像素带来的特征高维数问题同时不丢失图像的局部信息，本文根据数据库样本尺寸，对每张64×128大小的行人数据库图像进行金字塔3层分割。即按照样本尺寸，按1×1、2×2、4×4的比例分割后，可以得到1+2×2+4×4=21个3种不同尺度的小块；对每张48×48大小的遥感车辆和飞机数据库图像进行金字塔3层分割，即按照样本尺寸，按1×1、3×3、4×4的比例分割后，可以得到1+3×3+4×4=26个3种不同尺度的小块，再遍历每个小块内的像素值。下面主要讲解行人数据库处理小块的方法，遥感车辆和飞机数据库处理小块的方法与之一致。

根据统计直方图的思想，对于金字塔分割后的每个小块，依次遍历像素计算小块的LBP特征，对小块每个像素点的LBP二值化矢量值进行逻辑函数运算。根据上文定义，计算后可得到新的n位LVP值，共有2n类，统计小块中每类矢量值对应2n类中的占比，于是得到由2n个类别占比组成的2n维特征向量，将所有21个小块得到的2n维向量分别归一化后互相串联，即可得到21×2n维逻辑处理后的特征向量。

(a) 行人正样本

(b) 行人负样本

(c) 车辆正样本

(d) 车辆负样本

(e) 飞机正样本

(f) 飞机负样本

以八位的LBP特征值为例，不同逻辑块长度和重叠百分比对应的LVP特征维数大小见表2。

表2 行人数据库中不同逻辑区域处理后的特征维数

3.3 实验结果分析

本文主要分析在行人数据库上测试后的实验结果。实验选取2 416个正样本和4 584个负样本作为训练样本，剩下1 126个正样本和1 874个负样本作为测试样本。利用三层BP神经网络来训练行人样本得到行人分类器，用此分类器对测试样本进行测试，对比原始特征和经过矢量变换后的测试精度来对本文提出的改进方法进行验证。

本文用TP表示将正样本预测为正样本的样本个数，FN表示将正样本预测为负样本的样本个数，FP表示将负样本预测为正样本的样本个数，TN表示将负样本预测为负样本的样本个数，得到准确率F1，精度PR，召回率RR的公式如下:

(10)

(11)

(12)

按照计算原理对行人数据库进行LBP特征提取，使用初始化完成的三层BP神经网络进行训练测试，初始隐层节点数默认均为8个。表3列出了不同的LBP特征在行人测试样本库上的测试准确率F1。ELBP(1,8)表示圆形LBP的采样半径为1个像素，采样点数为8；ELBP(1.5,12)表示圆形LBP的采样半径为1.5个像素，采样点数为12。特征维数根据单个样本维数乘以块数得到。原256类LBP、圆形LBP维数是256×21=5 376；均值LBP(ULBP)的维数是59×21=1 239，LLP线段与样本图像的夹角为0°，由于是双线段，故LLP特征维数是均值LBP的两倍，即2 478。LVP使用β函数为fun1，使用块长为2，重叠比为0 %、 50 %和块长为3，重叠比为66.7 %的混合变换方法。可以发现使用LVP在较低维数下依然具有最高的正确率。圆形LBP的采样半径和采样点数越大，精度越低。采用59类的方法维数最低。

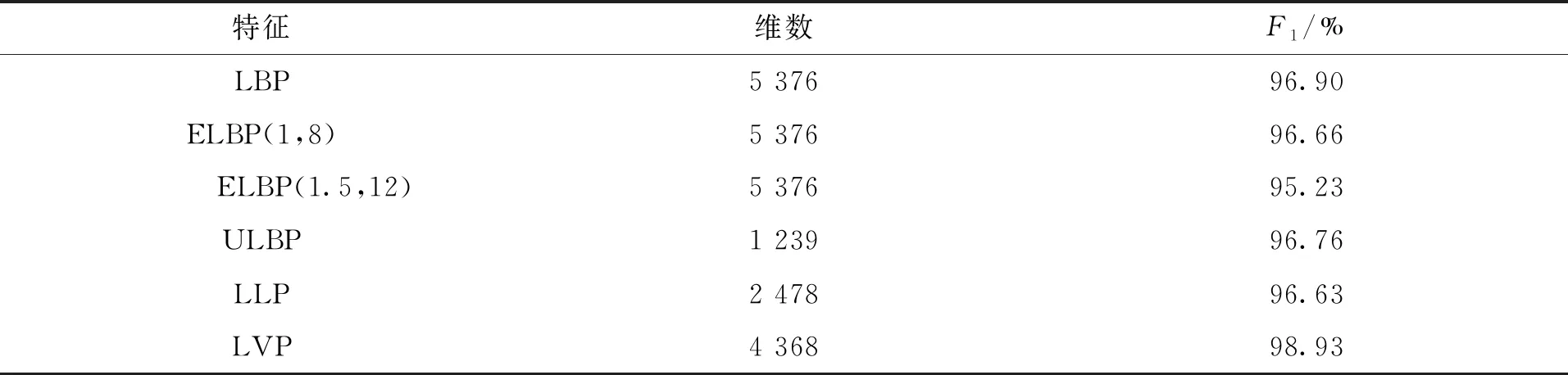
表3 不同LBP特征在行人数据库上的测试结果

表4给出了以原256类LBP特征为基础，局部块长度为2，重合百分比为0 %的LVP分类测试精度。由结果可以看出，以两位数不重合的区域进行逻辑运算后，特征的维数被明显减小，但测试精度整体上稍差，多种逻辑混合的方法中，或和与非、或非和与非结合效果比其他逻辑运算好。块长度为2，重叠百分比为0 %的LVP的召回率曲线见图6，可以看出多个逻辑组合的效果明显好于单个逻辑运算效果。

表4 局部块长度为2，重合百分比为0 %的LVP在BP神经网络上的测试结果

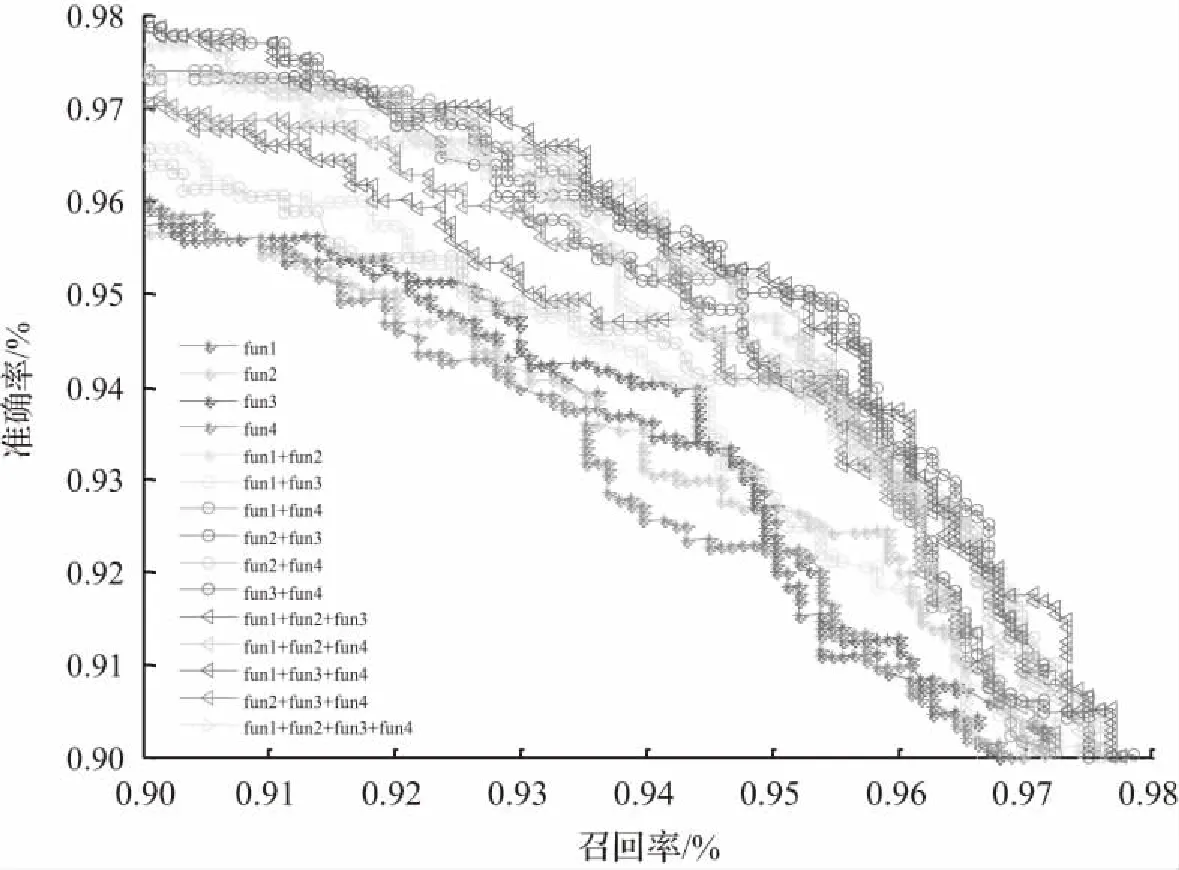
图6 局部块长度为2，重合百分比为0 %的LVP的召回率曲线

Fig.6 LVP’s recall rate curve as block length is 2 and overlap percentage is 0 %

表5给出了以原256类LBP特征为基础，局部块长度为2，重合百分比为50 %的LVP测试精度。结果显示，块重合百分比的增加对测试精度有了较明显的提高，其中或非(fun3)、与非(fun4)、或非和与非(fun3+fun4)的检测精度变化不大。

表5 块长为2，重合百分比为50 %的LVP在BP神经网络上的测试结果

局部块长度为2，重合百分比为50 %的LVP的召回率曲线见图7，可以看到使用逻辑或、与和或非逻辑函数组合具有很好的检测效果，四种逻辑混合的运算与之相差不大。或非和与非的运算即使单独使用或是结合在一起，逻辑运算效果都没有突出的表现。

图7 局部块长度为2，重合百分比50 %的LVP的召回率曲线

表6给出了两个块长度为2，重叠百分比为0 %，由双四位重组为八位的LVP分类测试精度。结果显示，除了或和或非(fun1+fun3)、与和与非(fun2+fun4)处理后的测试精度稍有下降外，其余逻辑处理后精度都有不同程度的提升。

表6 块长度为2，重叠百分比为0 %，由双四位重组为八位的LVP在BP神经网络上的测试结果

表7给出了以原256类LBP特征为基础，局部块长度为3，重合百分比为66.67 %的LVP分类测试精度。整体上来说，块长为3的逻辑运算后的测试精度并没有块长为2，有重叠比的运算后测试精度高，但是部分逻辑组合后可以达到较好的测试效果。

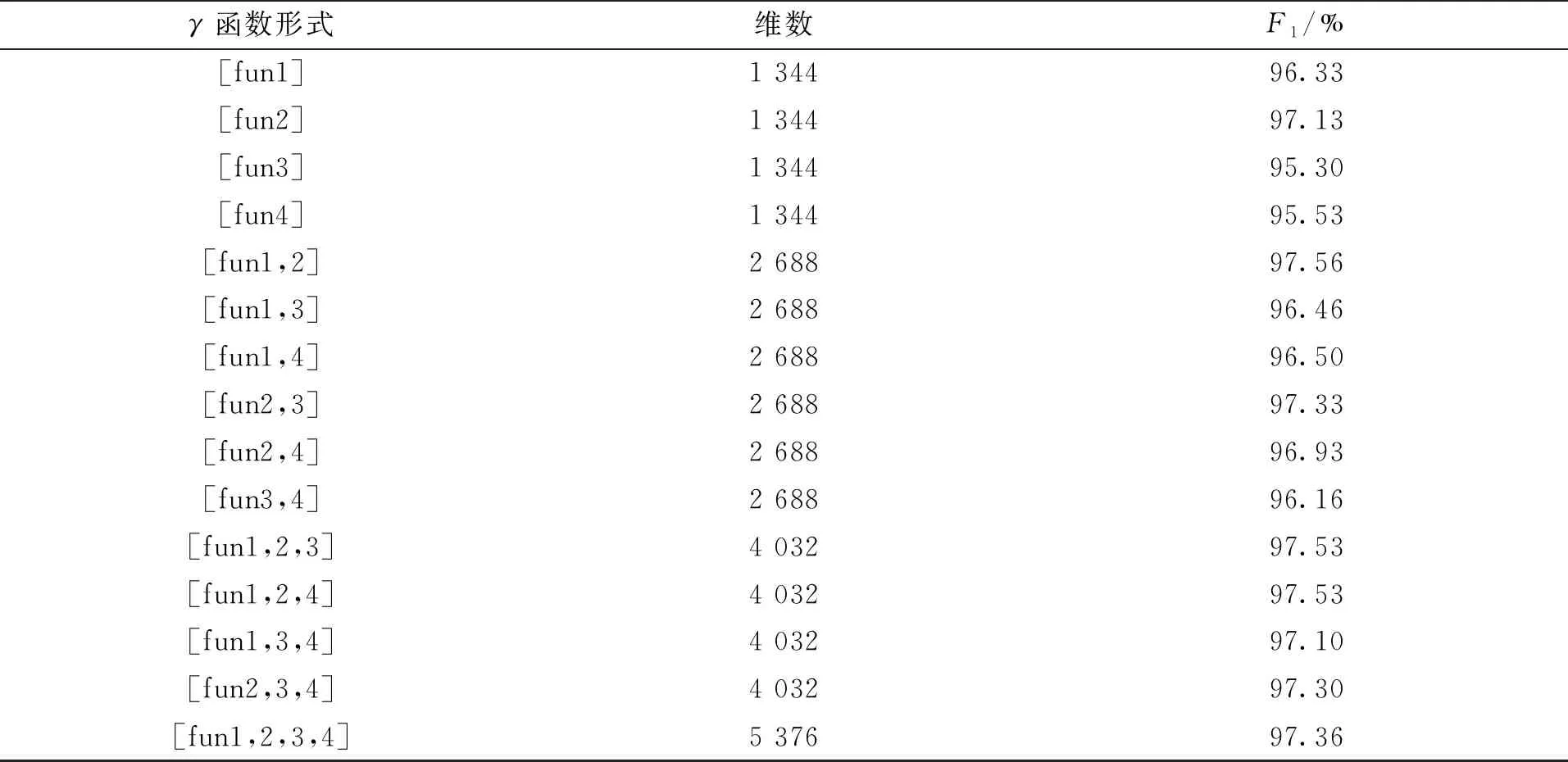
表7 局部块长度为3，重合百分比为66.67 %的LVP在BP神经网络上的测试结果

图8给出了局部块长度为3，重合百分比为66.67 %的LVP的召回率曲线，其中最好的是逻辑或和逻辑与的混合运算，单独的与非和或非运算后的结果最差，在混合逻辑运算中表现也不是很出色。

图8 块长为3，重叠比66.67 %的LVP特征的召回率曲线

表8给出了上述测试精度相对较高的块长为2，重叠比为50 %，γ函数为fun2的LVP在BP神经网络不同结构时的测试精度。表8中的BP(m,2)表示三层BP神经网络，隐层节点数为m,输出层节点数为2。本文实验选用了5种BP网络结构，结果显示隐层节点数为8时精度最高。

表8 LVP在不同BP网络上的准确率

从前文的分析知，单独使用逻辑或(fun1)和逻辑与(fun2)函数处理后的LVP检测精度相对较高，可以对同一个二值矢量进行多个块长度和块重叠百分比的与、或逻辑运算。表9给出了块长度为2，重叠比为0 %，50 %，以及块长为3，重叠比为66.67 %的LVP混合串联运算方法测试精度。可以看到混合块长度和对应重叠比能提高检测精度，其中块长度为2，重叠比为0 %，50 %，以块长为3，重叠比为66.67 %混合后的精度最好。

根据上述结论，通过逻辑运算的LBP分类方法能在一定程度上提高目标检测的精度。图9给出了混合使用3种不同块长度和对应重叠比的逻辑或和逻辑与LVP运算后原256类LBP特征的行人实际检测效果图。使用多尺度滑块的检测窗口，检测后采用非极大值抑制得到检测效果图。可以看出对图中完整的行人能有较好的识别能力。受到检测框定程序的一定影响，检测结果存在部分框定的偏差。

表9 3种逻辑区域混合的LVP在BP神经网络上的测试结果

图9 逻辑或和逻辑与LVP运算后的行人检测效果图

Fig.9 Test result on pedestrian database using LVP with logic-and and logic-or

为了体现该逻辑运算的适用性，本文对高清遥感卫星图像中的车辆和飞机目标进行检测，对48×48大小的样本进行1×1、3×3、4×4比例的金字塔分割，其余操作与行人数据库一致。图10给出了混合使用三种不同块长度和对应重叠比的逻辑或和逻辑与LVP运算后原256类LBP特征的车辆和飞机实际LVP检测效果图，检测方法与上述行人检测方法一致。结果显示，绝大部分的飞机和车辆都能被识别，少部分误测发生在与目标相似度极高的情况下，说明该分类方法具有一定通用性。

通过上述的实验可以得出，在使用单独逻辑块长度运算时，使用块长为2，重叠比为0 %的LVP检测精度最低，块长为3的LVP检测精度开始下降，两者相对于检测效果最好的块长为2，重叠比为50 %的LVP来说，逻辑函数运算的区域减少，说明逻辑运算区域的减少将增加二值信息的细节损失，而使用3种逻辑块长度混合的方法能更有效增加二进制值细节信息，增加LBP的模式种类。比较4种逻辑函数形式，采用逻辑或和逻辑与的测试精度具有较大优势，所以采用两种逻辑函数结合的方法能深度挖掘二值信息。比较四类LBP特征，原256类LBP特征依然具有较高的检测精度，圆形LBP受到了采样半径扩大后的影响，信息表达不全面；均值LBP和LLP受到59类归类的影响，减少了两次以上跳变的二值信息，降低了检测的精度。

为了对比该矢量变换的方法对二值化矢量的分类均衡性，在三个数据库的前两百张样本中使用原256类LBP、59类LBP和混合逻辑块长度运算后的208类LVP(块长为2，重叠比0 %的16类、块长为2，重叠比50 %的128类和块长为3，重叠比66.7 %的64类结合)分别做特征提取，对应类别归类。对比各类别中的占比中位数、类标准差和最大占比。占比中位数是对各类占比按大小顺序排列后，排列于中间的类的占比，可以直观看出中间数据以及与最大最小值的差距；类标准差是各类占比与平均值差值平方和的开方，用于表现各类占比的波动大小，其中不同类的占比平均值为1/总类数。最大占比是所有类中占比最大的值，用于与占比中位数比较。按照上述方法对三种数据库前500个正负样本处理归类后，得到的数据如表10所示。三种情况下，类最小占比均为0，此处未列出。

图10 逻辑或和逻辑与LVP运算后车辆、飞机数据库检测效果图

在表10中可以看到59类LBP在忽略了两次以上的跳变后导致信息缺失的同时，还导致了分类的极度不平衡；256类LBP虽然没有信息损失，但由于分类类别过多，二值化矢量分类也极端不平衡，占比中位数和类最大占比差距有时可达上百倍，远不是期望的分类均衡效果。混合逻辑块长运算后的208类LVP在保持了全部像素信息的同时，占比中位数和类最大占比的差距也只有十几倍，可见该分类方法将LBP种类的均衡性大大提高，特征得到了加强。

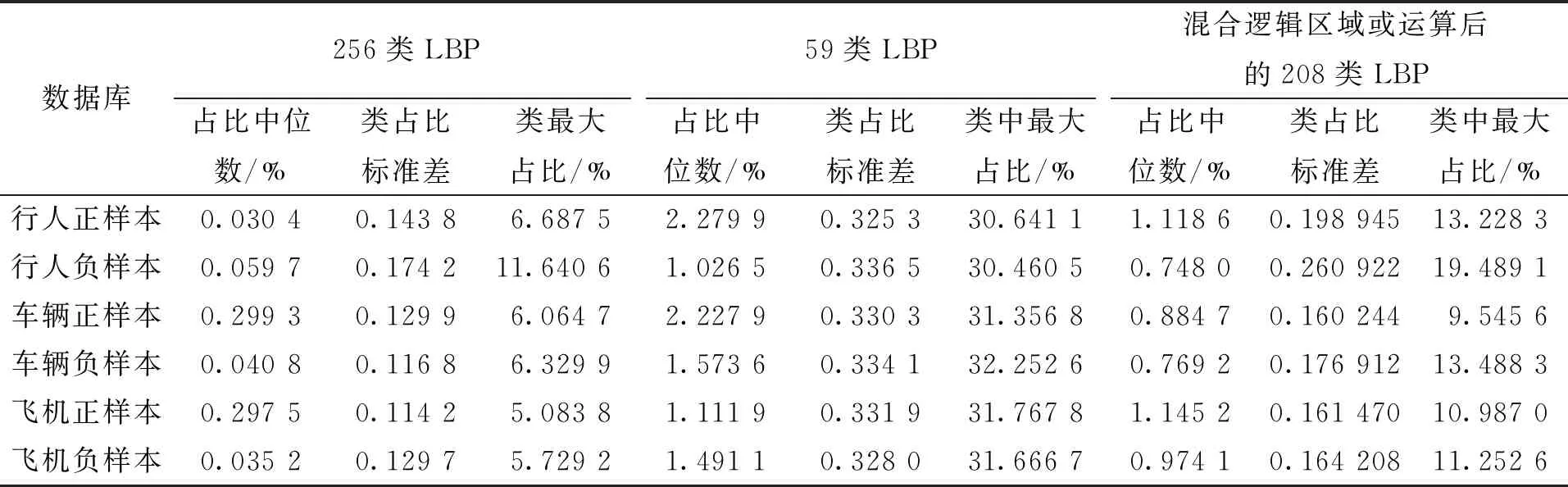
表10 3种类别的LBP归类数据表

4 结语

本文研究了一种基于矢量变换运算的局部二值化模式目标分类方法。针对局部二值模式存在的分类不平衡和分类信息丢失的问题，使用区域逻辑函数运算的方法对LBP二值矢量进行不同块区域、不同逻辑形式的运算，加强LBP特征的二值信息表达和分类平衡。对公用数据库INRIAPerson行人数据库和GUI_image遥感车辆、遥感飞数据库测试发现，局部二值矢量特征LVP下，当逻辑运算β函数为fun1，使用块长为2，重叠比0 %、 50 %和块长为3，重叠比66.7 %混合变换方法效果最好，在行人数据库中，或运算识别正确率提升了2.03 %，达到98.93 %；在车辆数据库中，用该方法使正确率提高了3.70 %，达到94.15 %；在飞机数据库中，用该方法使正确率提高了4.65 %，达到94.10 %。说明基于矢量变换的局部二值化模式分类方法对LBP特征有较好的改进效果，具有一定的实用价值。