基于分形理论的赫巴流体在多孔介质中的渗流模型
2020-07-13冯兴法
杨 仙,卢 伟,金 新,陈 娟,冯兴法
基于分形理论的赫巴流体在多孔介质中的渗流模型
杨 仙1,卢 伟1,金 新2,3,陈 娟4,冯兴法5
(1. 湖南科技大学 资源环境与安全工程学院,湖南 湘潭 411201;2. 中煤科工集团西安研究院有限公司,陕西 西安 710077;3. 中南大学 地球科学与信息物理学院,湖南 长沙 410000;4. 湖南科技大学 信息与电气工程学院,湖南 湘潭 411201;5. 中煤科工集团重庆设计研究院有限公司,重庆 400016)
泥浆是一种用途广泛的工程浆液,在工程施工过程中会渗流进入地层,给工程带来一定的影响。为深入研究泥浆的渗流机理,把地层模拟为多孔介质,泥浆模拟为能更全面地反映其流变性能的赫巴流体,基于分形理论,建立赫巴流体在多孔介质中的渗流模型。基于渗流模型计算结果,详细分析压力梯度、流性指数、稠度系数及孔隙率等参数对多孔介质中赫巴流体瞬时平均流速的影响,指出流速变化与压力梯度、流性指数及稠度系数的变化均呈幂指数关系,与孔隙率变化呈二项式关系,且流性指数是一个影响赫巴流体渗流速度的极敏感因素。渗流模型计算结果为相关工程中泥浆方案的设计与施工奠定了一定的理论基础。
泥浆;赫巴流体;多孔介质;分形理论;渗流模型
泥浆是一种用途广泛的工程浆液,其在钻井工程、顶管工程、钻孔灌注桩和地下连续墙等施工中都是必不可少的[1-2]。工程施工过程中,泥浆会渗流进入地层,给不同的工程带来有利或不利影响。建立泥浆在地层中的渗流模型,深入研究其渗流机理,有利于在施工过程中更好地控制渗流过程,增加渗流的有利影响,减小其不利影响。要建立泥浆渗流模型,首先需要选择泥浆流变模型。当前,研究者们常采用宾汉流体和幂律流体描述泥浆的流变性能[3-4]。宾汉流体多用于表征泥浆的塑性特征,幂律流体多用于表征泥浆的假塑性特征,宾汉流体和幂律流体均可看作赫巴流体的一种特殊形式。赫巴模型既能反映泥浆的塑性特征,又能反映其假塑性特征[5],比宾汉模式和幂律模式更全面,对于塑性和假塑性均较为明显的泥浆,采取赫巴流体进行模拟更为合适,准确率最高[6]。分形理论是数学家本华·曼德博首先提出的,即用分形分维的数学工具来描述研究客观事物[7]。众多研究者指出岩土介质适宜于使用分形理论来进行研究:C. Sparrow[8]指出天然多孔岩土体往往具有良好的分形特征;D. Avnir 等[9]提出了岩土多孔介质具有分形特征的概念;J. P. Hansen等[10]用盒子法测得了砂岩的分形维数;A. J. Katz等[11]和C. E. Krohn[12]基于SEM实验,结合分形理论表征出砂岩的孔隙结构;郁伯铭团队较全面地论述了多孔介质输运性质的分形分析理论[13-17];员美娟等[18]基于服从分形分布的弯曲毛细管束模型,运用分形几何理论推导出卡森流体在多孔介质中流动的流量、流速、启动压力梯度和有效渗透率的分形解析解;万秀峰[19]在研究砂卵石地层水泥–水玻璃复合注浆加固时,基于分形理论,把浆液简化为宾汉流体,推导其在地层中的渗透模型;周子龙等[20]根据分形理论推导出孔隙通道的曲折效应方程,并通过幂律流体本构方程导出考虑孔隙曲折效应的浆液扩散模型。由上述研究可以看出,已有研究基于分形理论,把工程浆液模拟为宾汉流体和幂律流体,研究其在岩土体中的渗流机理。考虑到对于某些塑性和假塑性均较为明显的泥浆,采取赫巴流体描述流体特性更全面、更准确,本研究中把地层岩土体简化为多孔介质,泥浆模拟为赫巴流体,基于分形理论建立了赫巴流体在多孔介质中的渗流模型,并对其计算结果进行详细分析。
1 赫巴流体在单根圆直管中的渗流模型
要研究赫巴流体在多孔介质中的渗流模型,首先,需要研究赫巴流体在圆直管中的渗流模型。赫巴流体在圆直管中的渗流情况如图1所示。
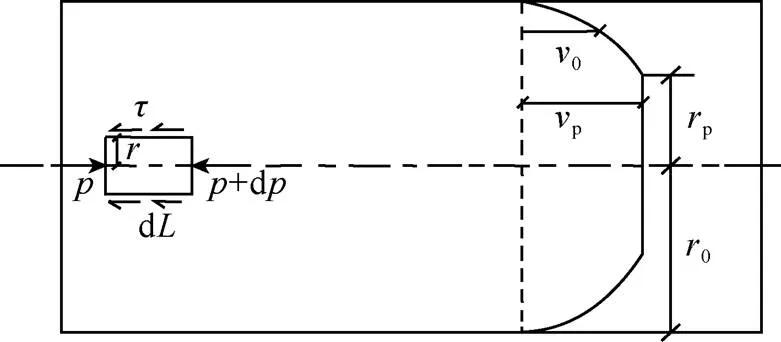
图1 赫巴流体在圆直管中的渗流示意
在图1中,针对流体单元柱元素,有如下表达式:
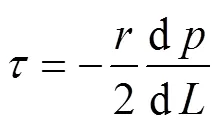
式中:为注浆压力;为流体流经的距离;为剪切应力;为径向距离;d/d为压力梯度。
赫巴流体本构方程:

由式(1)和式(2)得到:
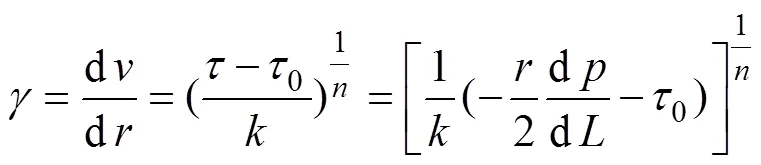
当0≤≤p时,每一层流体相对于邻层,保持静止状态,速度均相等。当p<≤0时,每一层流体相对于邻层,保持运动状态,速度不相等。
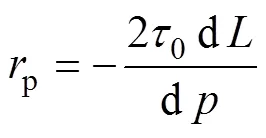
假设赫巴流体的流动方式为层流,则边界条件为:当=0时,=0。
当p<≤0时:
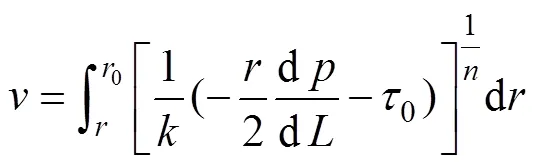
结合边界条件及式(4)和式(5),可得:

当0≤≤p时:
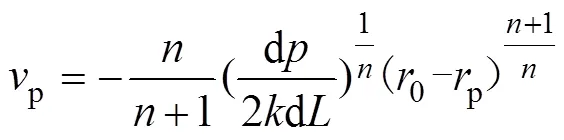
假设

圆管中,赫巴流体的流量是通过相对静止区(0≤≤p)和相对运动区(p<≤0)两部分的流量总和:
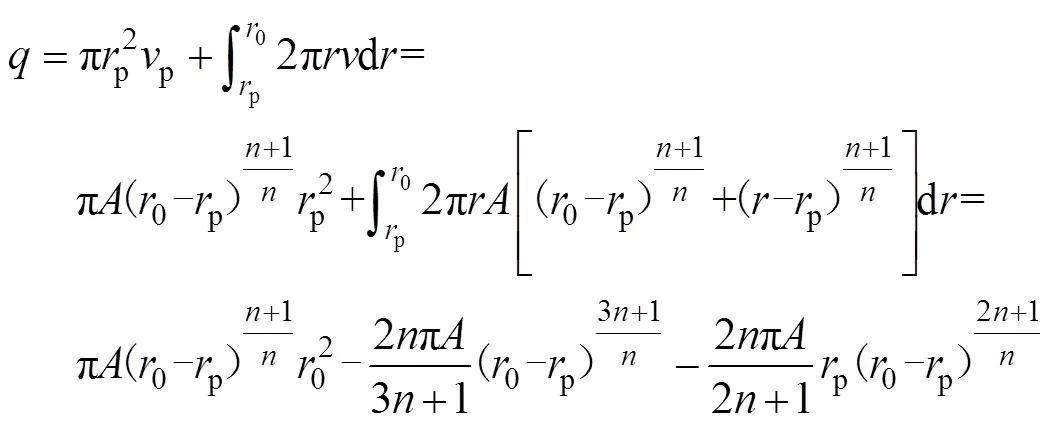
式中:0为管道半径;p为塞流层半径;p为塞流层流速;为单管流量。
2 多孔介质分形理论基础
根据分形理论,多孔介质孔隙大小分布在一定范围内,且在统计上满足分形标度关系[21]:

式中:表示尺度;()表示物体的体积、面积、质量或曲线长度等指标;f为分形维数,取值0~2。分形物体累计数与颗粒大小的分布也满足如下的标度关系[21]:
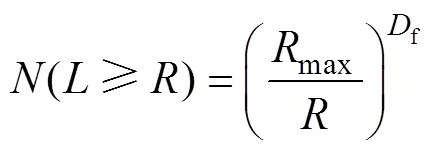
式中:max为最大孔隙尺寸;为孔隙尺寸。
对式(11)进行微分,得到:
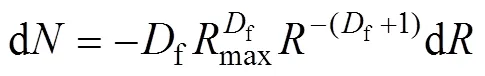
多孔介质的随机弯曲通道长 度T可根据分形理论得出[17]:
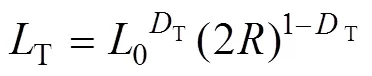
式中:0为通道的直线长度;T为迂曲度分形维数;T=1时表示毛细通道是直线;T取值范围为1~2。从式(13)可以看出,T和半径有关,越大,则T越小。
对式(13)微分可得到:

孔隙分形维数计算f公式如下[17]:

多孔介质迂曲度分形维数T计算公式如下[17-20]:

流线迂曲度的表达式为[17-20]:
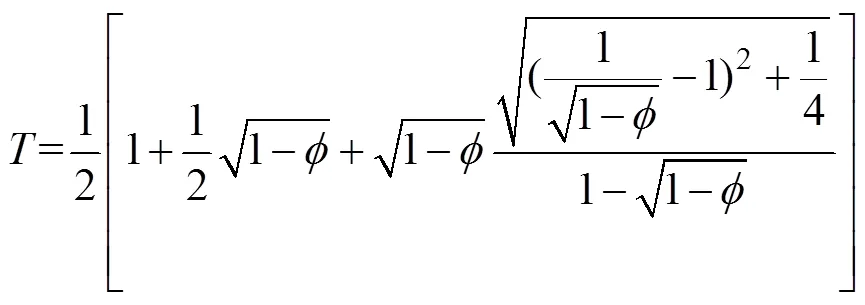
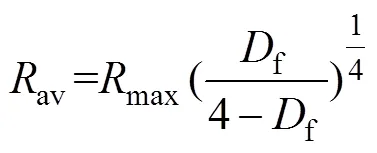
多孔介质的结构参数计算公式为[17]:
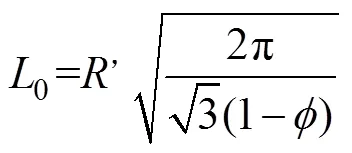
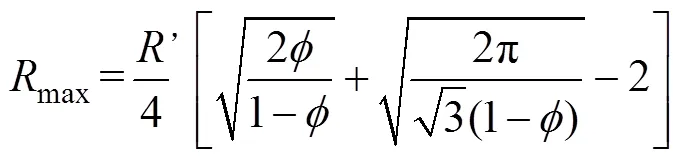
式中:,为多孔介质的平均粒径。
多孔介质的结构参数对于流体在多孔介质中的渗流影响很大。如,单个孔隙大小直接影响渗透率和渗流速度,小孔体积占岩样孔隙总体积的比例越大,其渗透率和渗流速度就越小。根据毛管模型理论与达西定律的关系可知,渗透率的平方根与平均孔隙半径成正比[22]。在分形理论中,充分考虑了多孔介质的结构参数问题,因此,新建立的渗流模型能够更好地表征实际渗流情况。
3 赫巴流体在多孔介质中的渗流模型
在多孔介质中,流体实际渗流路径有一定的随机性,可看作是弯曲管道中的渗流,如图2所示。

图2 赫巴流体在多孔介质中的渗流示意
因此,在式(8)中用T代替,并假设:

则:
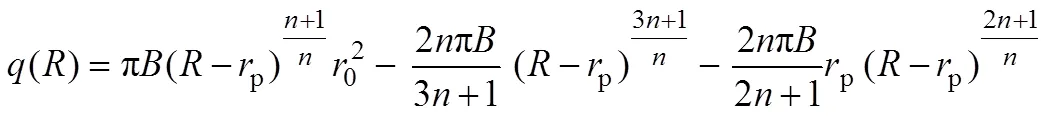
3.1 赫巴流体在多孔介质中的流量
由于多孔介质中弯曲的管道大小不一,且在统计学上服从分形幂规律,因此,多孔介质横截面的总流量可以通过积分计算得到:
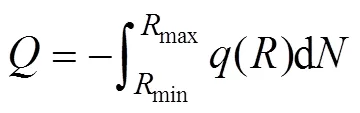
式中:为多孔介质横截面的总流量。
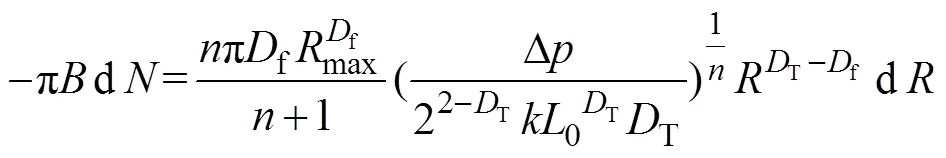
假设:
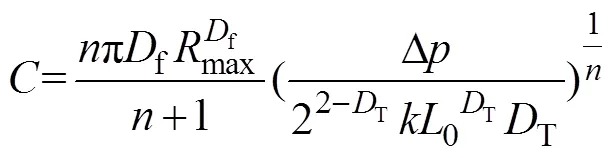
则:
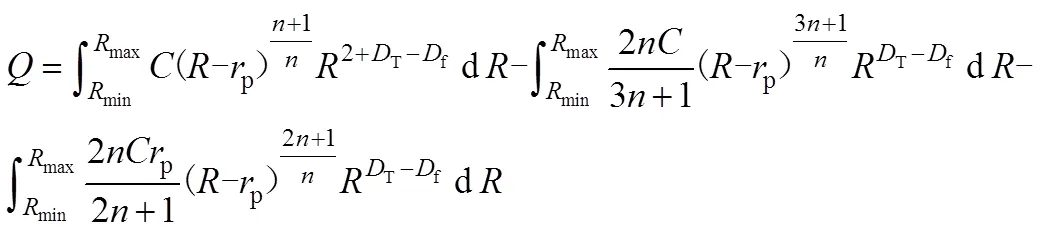
该积分没有解析解,可使用MATLAB计算其数值解。
3.2 赫巴流体在多孔介质中的流速
多孔介质横截面积的计算公式如下:
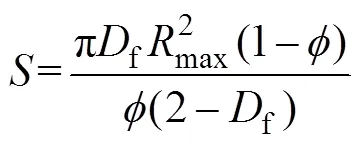
式中:为多孔介质的横截面积。
用式(26)除以式(27)即可得到赫巴流体在多孔介质中的平均速度。
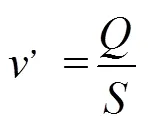
4 模型计算结果与分析
4.1 流速与压力梯度之间的关系


图3 流速随压力梯度的变化关系
由图3可以看出,压力梯度与流速之间的关系符合幂指数关系,随着压力梯度的增加,流速逐步增加,且流速增加的趋势越来越明显,这与实际工程中的状况是一致的。本模型计算的是单位时间的流量和瞬时流速,因此,把压力梯度作为一个常量代入式(28)。但在实际工程中,如注浆等施工时,随着浆液从注浆口往多孔介质弯曲通道中的扩散时间和扩散距离的增加,压力梯度是逐步降低的。因此,如果涉及到注浆时间累积的计算时,压力梯度不能当作常量进行计算。
4.2 流速与n、k值之间的关系
当赫巴流体本构方程的相关参数=0.9,0=10 Pa时,变化值,通过式(2)计算其剪切应力。当旋转速度为600 r/min(1 022 s–1)时,不同值对应的赫巴流体剪切应力见表1。

表1 n值变化时赫巴流体剪切应力计算值

当赫巴流体本构方程的相关参数=0.6,0=10 Pa时,变化值,通过式(2)计算其剪切应力。当旋转速度为600 r/min(1 022 s–1)时,不同值对应的赫巴流体剪切应力见表2。


图4 流速随流性指数n值的变化关系

表2 k值变化时赫巴流体剪切应力计算值
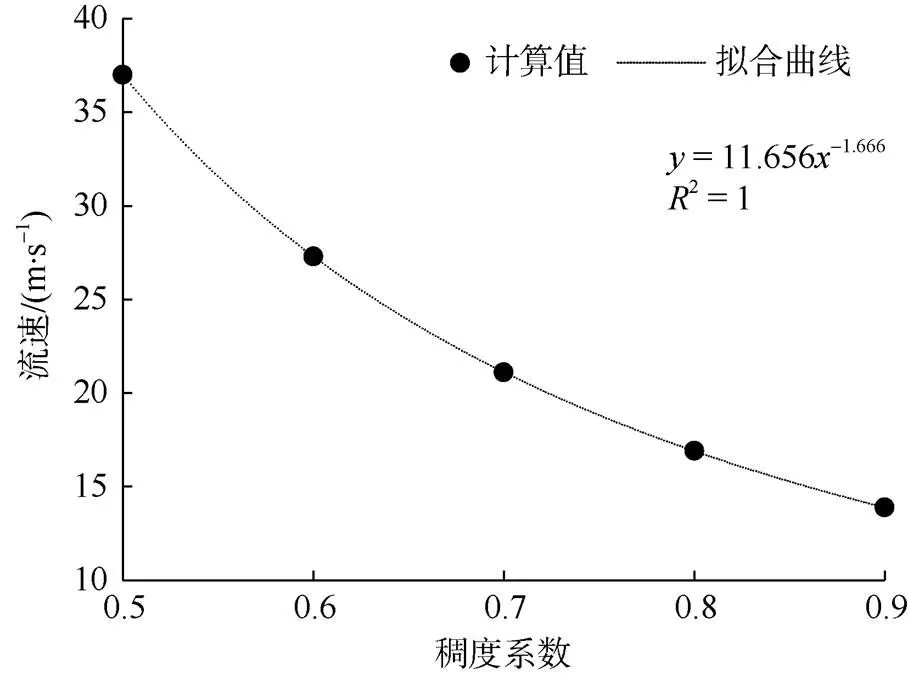
图5 流速随稠度系数k值的变化关系
由图4、图5可以看出,流速与赫巴流体本构参数、值之间的关系均呈幂指数关系。结合表1、表2可知,、值越大,剪切应力越大,流速越小。值变化比值变化对剪切应力影响更大,值变化对流速的影响也更大。结合图4、图5中曲线趋势及式(2)可知:当值不变、值变化,或值不变、值变化,使得两种赫巴流体的剪切应力相同时,值小的流体,其流速会远大于值更小的流体。由此可见,对于赫巴流体流速而言,值的变化是一个极敏感因素。由此可知,要更好地控制泥浆在多孔介质中的渗流,简单地控制黏度不一定能达到预期的目的,更为科学的方法是综合控制、值,特别是选取合适的值范围,对流体渗流速度影响很大。
4.3 流速与孔隙率之间的关系
图6为根据式(28)计算出来的流速随孔隙率的变化关系。选取的计算参数有:赫巴流体本构方程的相关参数=0.6,=0.9,0=10 Pa;计算选取的多孔介质相关参数有max=0.05 m,min=0.000 5 m;压力梯度d/d=200 kPa/m。
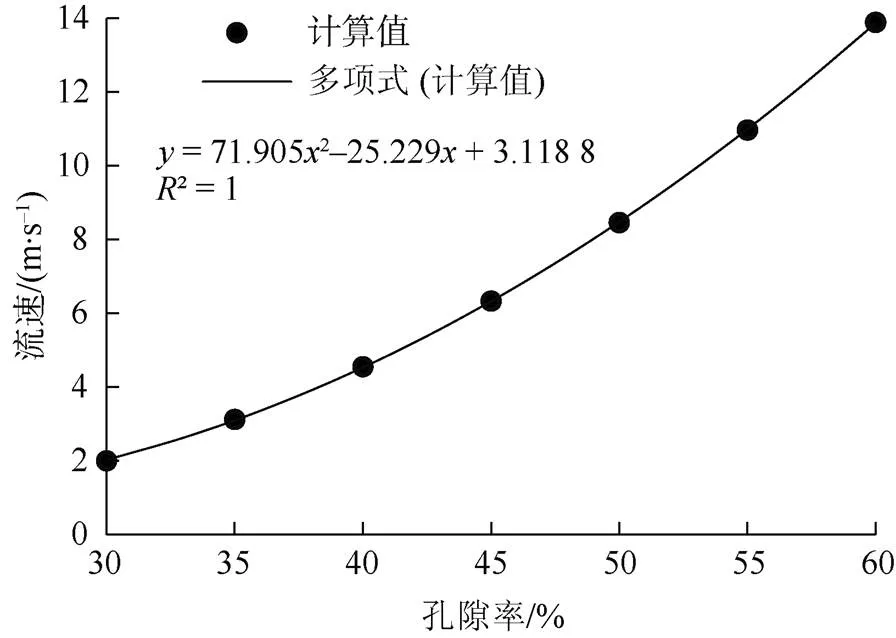
图6 流速随孔隙率的变化关系
由图6可以看出,流速与多孔介质孔隙率之间的关系呈二项式关系,孔隙率越大,流速越大,且随着孔隙率的增加,流速增加的趋势越来越明显。当孔隙率由30%增加到45%时,流速增加2.3倍;当孔隙率由30%增加到60%时,流速增加7倍。这也解释了在实际工程中孔隙率对渗流影响极大的深层原因。
本节中根据所建立的赫巴流体在多孔介质中的渗流模型,着重对施工参数(压力梯度)、流体特性参数(、值)以及岩土体特性参数(孔隙率)等对瞬时渗流平均流速的影响进行了计算与分析,计算结果与实际工作状况相吻合。基于建立的渗流模型,还可以进一步分析流体的启动压力梯度、有效渗透率等与各类参数之间的关系;引入时间因子,还能进一步建立渗流扩散模型,研究泥浆在岩土体中的扩散半径、扩散过程中压力的衰减以及渗流全程平均流速变化规律等。
5 结论
a. 把地层简化为多孔介质,泥浆模拟为赫巴流体,基于分形理论,建立了赫巴流体在多孔介质中的渗流模型,并对渗流模型的计算结果进行了分析研究。研究结果显示,压力梯度、赫巴流体本构参数及地层孔隙率均会对渗流流速产生影响。
b.压力梯度与流速之间的关系符合幂指数关系,随着压力梯度的增加,流速逐步增加,且流速增加的趋势越来越明显;流速与赫巴流体本构参数、值之间的关系均呈幂指数关系,、值越大,剪切应力越大,流速越小,且为一个极敏感因素;流速与多孔介质孔隙率之间的关系呈二项式关系,孔隙率越大,流速越大,且流速增加的趋势越来越明显。
c.为了更好地控制泥浆在地层中的渗流,可以基于建立的渗流模型,在施工参数及泥浆配置方面提出一些措施。且泥浆配置过程中,需综合控制、值,特别是选取合适的值范围,简单地控制流体黏度可能达不到预期目的。
d.基于建立的渗流模型,引入时间因子,则可进一步建立渗流扩散模型,对渗流扩散半径、渗流扩散过程中的压力衰减、渗流全程平均流速等进行更为全面深入的研究。
请听作者语音介绍创新技术成果等信息,欢迎与作者进行交流

[1] 莫世扬,杨晓伟,洪元堂,等. 非开挖顶管工艺在公路污水管线下穿工程中应用分析[J]. 公路工程,2019,44(2):151–155. MO Shiyang,YANG Xiaowei,HONG Yuantang,et al. Application analysis of trenchless pipe jacking technology in highway sewage pipeline project[J]. Highway Engineering,2019,44(2):151–155.
[2] 邓利蓉,刘振兴,曹钧,等. 硬岩破碎地层高温钻孔钻进的钻井液实验研究[J]. 煤田地质与勘探,2015,43(4):117–119. DENG Lirong,LIU Zhenxing,CAO Jun,et al. Experiment of drilling fluid used to drill hard fractured complex formation[J]. Coal Geology & Exploration,2015,43(4):117–119.
[3] 侯璐瑶,王奎升,侯世全. 基于宾汉模式的桥梁桩基钻孔泥浆流变特性初步研究[J]. 铁道建筑,2010(6):41–43. HOU Luyao,WANG Kuisheng,HOU Shiquan. Preliminary study on rheological properties of drilling mud from Bingham model to bridge pile foundation[J]. Railway Engineering,2010(6):41–43.
[4] 蔡亮学. 水平定向钻管道穿越回拖过程动态力学特性研究[D]. 东营:中国石油大学(华东),2011. CAI Liangxue. Investigation on dynamics of pipe during pullback in horizontal directional drilling installations[D]. Dongying:China University of Petroleum(East China),2011.
[5] 汪友平,郑秀华,夏柏如,等. 圆管中赫巴流体层流流动规律的研究[J]. 钻井液与完井液,2008,25(1):27–28. WANG Youping,ZHENG Xiuhua,XIA Bairu,et al. Studies of the laminar flow of Herschel-Bulkley fluids in pipes[J]. Drilling Fluid and Completion Fluid,2008,25(1):27–28.
[6] 李鑫,高德利,刁斌斌,等. 基于赫巴流体的页岩气大位移水平井裸眼延伸极限分析[J]. 天然气工业,2016,36(10):85–92. LI Xin,GAO Deli,DIAO Binbin,et al. Analysis on the open-hole extension limit of a shale-gas extended-reach horizontal well based on Hershel-Bulkley fluids[J]. Natural Gas Industry,2016,36(10):85–92.
[7] MANDELBROT B B. How long is the coast of britain? statistical self-similarity and fractional dimension[J]. Science,1967,156(3775):636–638.
[8] SPARROW C. The fractal geometry of nature by B. Mandelbrot[J]. Journal of the Royal Statistical Society,1984,147(4):616–618.
[9] AVNIR D,FARIN D,PFEIFER P. Chemistry in non-integer dimensions between two and three. II. Fractal surfaces of adsorbents[J]. The Journal of Chemical Physics,1983,79(7):3566–3571.
[10] HANSEN J P,SKJELTORP A T. Fractal pore space and rock permeability implications[J]. Physical Review B Condensed Matter,1988,38(4):2635–2638.
[11] KATZ A J,THOMPSON A H. Fractal sandstone pores:Implications for conductivity and pore formation[J]. Physical Review Letters,1985,54(12):1325–1328.
[12] KROHN C E. Sandstone fractal and euclidean pore volume distributions[J]. Journal of Geophysical Research:Solid Earth,1988,93(B4):3286–3296.
[13] 吴金随. 多孔介质里流动阻力分析[D]. 武汉:华中科技大学,2007. WU Jinsui. Analysis of resistance for flow through porous media[D]. Wuhan:Huazhong University of Science and Technology,2007.
[14] 邹明清. 分形理论的若干应用[D]. 武汉:华中科技大学,2007. ZOU Mingqing. Fractal theory and its applications to porous media, rough surface and thermal contact conductance[D]. Wuhan:Huazhong University of Science and Technology,2007.
[15] YU B M. Fractal character for tortuous stream tubes in porous media[J]. Chinese Physics Letters,2005,22(1):158–160.
[16] XU P,YU B M. Developing a new form of permeability and Kozeny-Carman constant for homogeneous porous media by means of fractal geometry[J]. Advances in Water Resources,2008,31(1):74–81.
[17] LI J H,YU B M. Tortuosity of flow paths through a Sierpinski carpet[J]. Chinese Physics Letters,2011,28(3):117–119.
[18] 员美娟,郁伯铭,郑伟,等. 多孔介质中卡森流体的分形分析[J]. 物理学报,2011,60(2):410–415. YUAN Meijuan,YU Boming,ZHENG Wei,et al. Fractal analysis of Casson fluid flow in porous media[J]. Acta Physica Sinica,2011,60(2):410–415.
[19] 万秀峰. 砂卵石地层水泥–水玻璃复合注浆加固关键技术研究[D]. 长沙:中南大学,2014. WAN Xiufeng. Gordian technique of cement and sodium silicate composite grouting reinforcement in sand gravel strata[D]. Changsha:Central South University,2014.
[20] 周子龙,杜雪明,陈钊,等. 考虑孔隙曲折效应的浆液扩散压力[J]. 中国有色金属学报,2016,26(8):1721–1727. ZHOU Zilong,DU Xueming,CHEN Zhao,et al. Grout dispersion considering effect of pore tortuosity[J]. The Chinese Journal of Nonferrous Metals,2016,26(8):1721–1727.
[21] CRAWFORD J W,MATSUI N. Heterogeneity of the pore and solid volume of soil:Distinguishing a fractal space from its non–fractal complement[J]. Geoderma,1996,73(3/4):183–195.
[22] 黄延章. 低渗透油层渗流机理[M]. 北京:石油工业出版社,1998. HUANG Yanzhang. Seepage mechanism of the low permeability reservoir[M]. Beijing:Petroleum Industry Press,1998.
Fractal theory-based seepage model of Hershel-Bulkley fluid in porous medium
YANG Xian1, LU Wei1, JIN Xin2,3, CHEN Juan4, FENG Xingfa5
(1.School of Resource, Environment and Safety Engineering, Hunan University of Science and Technology, Xiangtan 411201, China; 2. Xi’an Research Institute Co. Ltd., China Coal Technology and Engineering Group Corp., Xi’an 710077, China; 3. School of Geosciences and Info-physics, Central South University, Changsha 410000, China; 4. School of Information and Electrical Engineering, Hunan University of Science and Technology, Xiangtan 411201, China;5. Chongqing Engineering Co. Ltd., China Coal Technology & Engineering Group Crop., Chongqing 400016, China)
Slurry is a kind of widely-used engineering fluid. Slurry will seeps into the formation in the process of construction, which has a certain impact on the project. In order to make deeper study on the seepage mechanism of slurry, the formation is simulated as porous medium, the slurry is simulated as Hershel-Bulkley fluid which can more comprehensively reflect its rheological properties, and the seepage model of Hershel-Bulkley fluid in porous medium was established based on Fractal theory. Based on the calculation results of seepage model, the effect of pressure gradient, flow index, consistency coefficient and porosity on the instantaneous average velocity of Hershel-Bulkley fluid in porous medium were analyzed in detail. It is pointed out that the change of velocity has a power exponential relation with the change of pressure gradient, flow index and consistency coefficient, and a binomial relation with the change of porosity. The results provide theory basics for design and construction of slurry grouting in relevant projects.
slurry; Hershel-Bulkley fluid; porous medium; fractal theory; seepage model

TE254.1
A
10.3969/j.issn.1001-1986.2020.03.018
1001-1986(2020)03-0122-06
2019-11-11;
2020-01-22
国家自然科学基金项目(51678226);湖南省自然科学基金项目(2019JJ50150)
National Natural Science Foundation of China(51678226);Natural Science Foundation of Hunan Province,China(2019JJ50150)
杨仙,1982年生,女,湖北天门人,博士,讲师,从事地下工程施工技术及环境影响研究.E-mail:yangxjj@163.com
金新,1982年生,男,陕西咸阳人,博士研究生,副研究员,从事煤矿井下坑道钻探技术与装备的研究和推广工作. E-mail:Jinxin@cctegxian.com
杨仙,卢伟,金新,等. 基于分形理论的赫巴流体在多孔介质中的渗流模型[J]. 煤田地质与勘探,2020,48(3):122–127.
YANG Xian,LU Wei,JIN Xin,et al. Fractal theory-based seepage model of Hershel-Bulkley fluid in porous medium[J]. Coal Geology & Exploration,2020,48(3):122–127.
(责任编辑 聂爱兰)
