浆液–风积沙双相介质充填材料堆积角度实验研究
2020-07-13白仲荣
白仲荣
浆液–风积沙双相介质充填材料堆积角度实验研究
白仲荣
(中煤科工集团西安研究院有限公司,陕西 西安 710077)
堆积角度是描述充填材料采空区内空间堆积形态的一个重要参数,对确定钻孔间距、优化浆液配置、调整注浆工艺参数具有重要的指导意义。为掌握浆液–风积沙双相介质充填材料堆积角度变化规律,采用尾矿自流堆积模型实验和流变特性实验,以风积沙的质量掺入比为变量,分别测定不同含砂率条件下浆料堆积参数和流变参数,并以此为基础对Sofra & Boger公式进行了回归修正,建立适合于浆液–风积沙双相介质充填材料的堆积角度计算式,为充填材料堆积角度定量评价提供了一条新途径。
采空区;堆积角度;风积沙;模型实验;流变特性
利用榆神府矿区丰富廉价的风积沙、粉煤灰作为空洞型采空区充填材料,在榆神府地区采空区灾害治理中得到了广泛的应用和推广[1-2]。水泥粉煤灰浆液及风积沙组成的介质在空洞中的堆积形态是采空区治理工程设计的重要依据。但前期研究方向主要集中在充填材料多样化[3-7]、工艺改进、充填材料流动性能等方面[8-9][9],而忽视充填材料在采空区内空间堆积形态方面的研究工作,导致钻孔间距和充填材料配比设计通常根据以往的工程经验确定,这种理论上的缺乏势必造成实践中的盲目性[10-11]。因此,研究充填材料在采空区内的堆积规律具有重要的理论意义和实际价值。本文以此为出发点,引用自流堆积模型实验和流变参数测定实验来探索和研究充填材料在采空区内的堆积规律,为后续采空区灾害治理中钻孔间距和充填材料配比设计提供更加充分的理论依据。
1 自流堆积模型实验
1.1 实验原理及方法
尾矿流体材料与浆液–风积沙充填材料均为双相介质,在流动和堆积形态方面具有显著的相似性。因此,本次实验采用Sofra & Boger 2001提出的尾矿堆积模型实验方法[12-15],对不同浆砂配比条件下的充填材料堆积角度变化规律进行研究。实验装置模型如图1所示。

图1 自流堆积模型实验装置示意

1.2 实验材料及配比
本次实验所用材料有水泥、粉煤灰、风积沙、水。其中,水泥为粉煤灰硅酸盐水泥,粉煤灰参量34%,密度为2.8 g/cm3;粉煤灰材料产自电塔镇阳关燃煤电厂,材料参数性能见表1。实验中选用风积沙作为充填骨料,产自府谷县庙沟门镇地区,堆积密度1.553 g/cm3,孔隙率为35.5%,其颗粒级配曲线如图2所示。

表1 粉煤灰性能参数值

图2 风积沙粒度分布
由图2可知,风积沙粒度成分以细砂(0.25~ 0.10 mm)为主,中砂(0.50~0.25 mm)次之,极细砂(0.10~ 0.05 mm)较少。大于0.50 mm和小于0.05 mm者含量极少。通过上述分析可知,本次实验所用天然风积沙中细粒级颗粒所占比重较大,粗粒级含量较少,为典型细砂,属不良级配[16-17]。
实验材料配比根据生产中常用配比及配置后料浆的性能确定,其中浆液中水固比为1︰1,水泥与粉煤灰质量比为2︰8。为了研究不同浆砂比条件下料浆堆积角度变化规律,以风积沙的质量掺入比为变量,砂子的参量由0逐渐递增至57%(表2)。
1.3 实验结果
根据材料配比和前述实验方法,进行自流堆积模型实验。实验结果见表2,自流堆积角度与含砂率之间的关系曲线如图3所示。
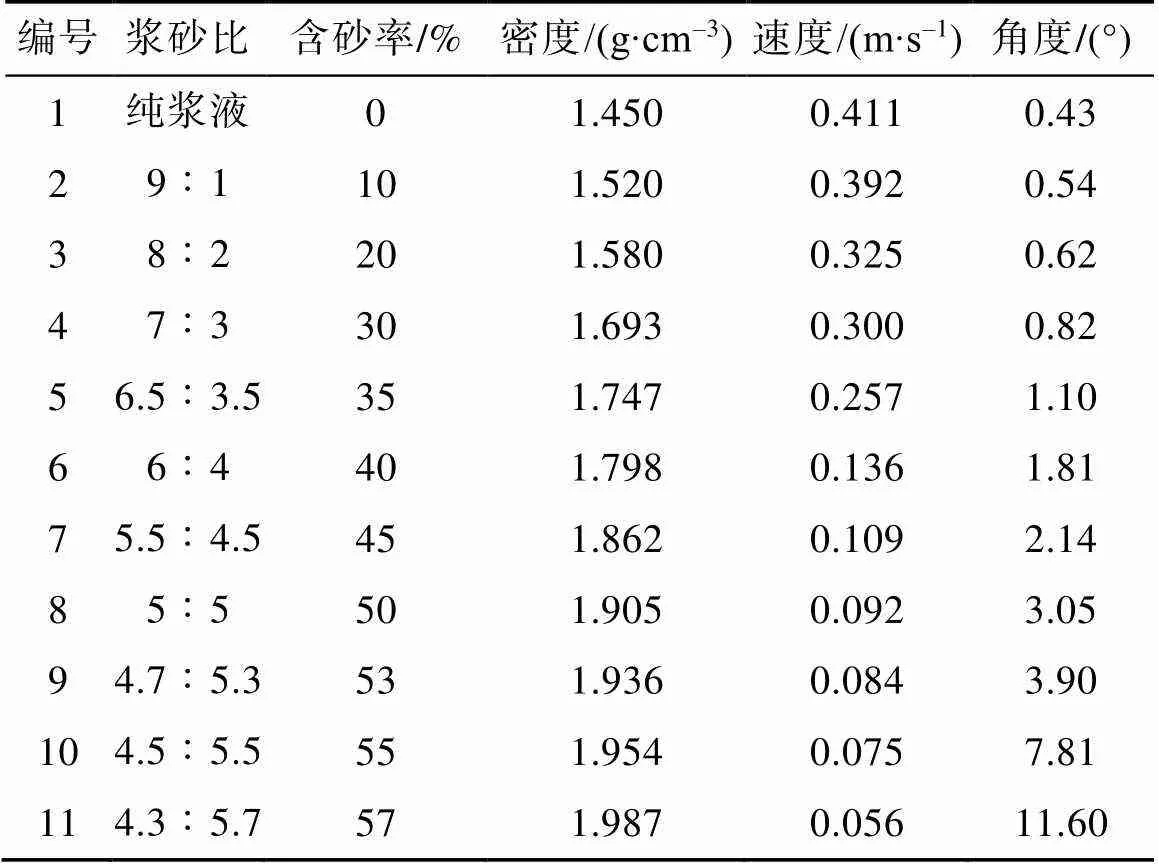
表2 料浆堆积角度数据

图3 料浆自流堆积角度与含砂率关系
由表2和图3可知,随着含砂率的增大,料浆堆积角度呈现出指数性增大的规律。根据变化曲线分解为3个区段:第一区段含砂率小于等于35%,在该区段内料浆自流堆积角度由0.43°增加至1.1°,递增趋势缓慢;第二区段含砂率为35%~53%,该区段内料浆自流堆积角度由1.1°增加至3.9°,递增趋势加快;第三区段含砂率为53%~57%,该区段内料浆自流堆积角度由3.9°增加至11.60°,递增趋势急剧加快。堆积角度增加过程中存在显著的“拐弯区间”含砂率,即料浆含砂率一旦超出该范围后,堆积角度急剧增大。本次实验“拐弯区间”含砂率为35%~53%,该值可以作为生产中均匀投砂比例的一个控制参数[10]。
2 流变参数测试实验
流变参数测试实验采用RST-CC桨式流变仪,并配备规格为V40-20的桨式转子,桨叶直径为20 mm,高度为40 mm,测试过程中剪切速率由0线性递增至60 s–1,测试时长60 s。测试结果如图4和图5所示。
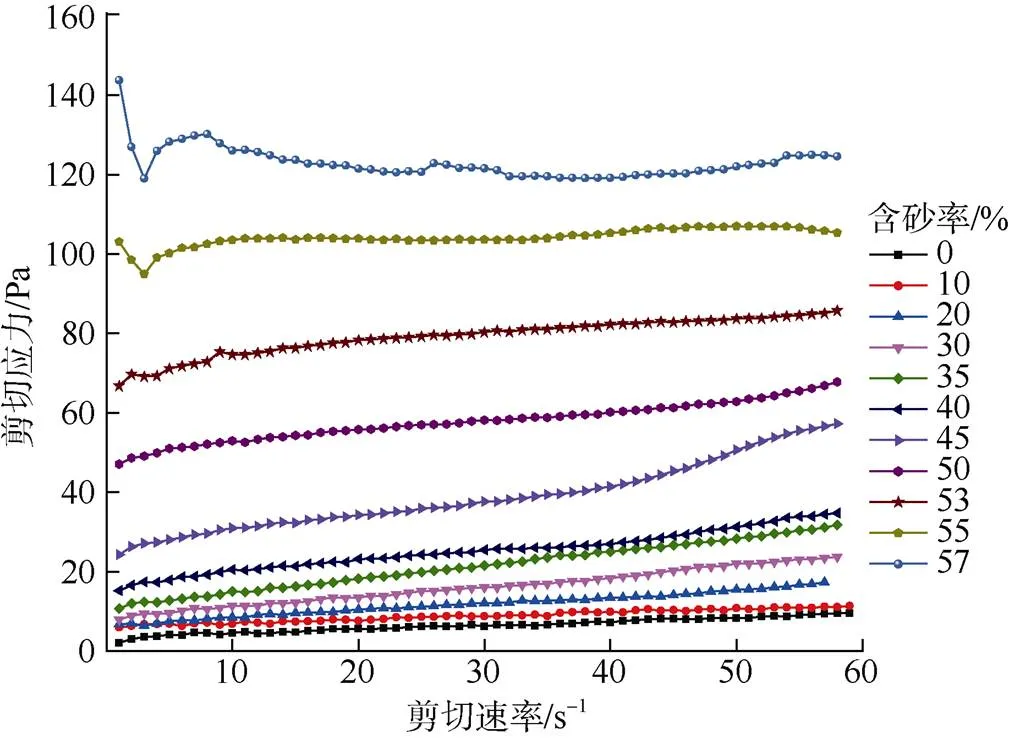
图4 剪切应力与剪切速率关系

图5 黏度与剪切速率关系


表3 料浆屈服应力及黏度参数
3 自流堆积角度计算
3.1 料浆自流角度公式检验
Sofra & Boger在2001年,从流变学、几何学、流速等角度出发,考虑材料屈服应力、黏度、密度、斜面宽度、流速等多方面的因素,结合模型实验提出了尾矿自流堆积角度计算公式[12-15]:

式中:为自流角度,(˚);0为屈服应力,Pa;为黏度,Pa·s;为密度,kg/m3;为流槽宽度,m;为重力加速度,m/s2;为流速,m/s。
将自流堆积模型实验和流变特性实验所测数据代入式(1)中检验其适用性,检验结果见表4,如图6所示。
由表4及图6可知,随着充填料浆含砂率的增大,堆积角度实测值与Sofra & Boger理论计算值相差越来越大,说明该公式适应性存在一定的范围。在引用之前需要根据实际应用对象特性进行回归分析,建立适合该对象的回归分析公式[19-20]。

表4 Sofra & Boger公式检验数据

图6 回归分析前理论值与实测值对比
3.2 料浆自流角度公式回归分析
由式(1)可知,影响自流堆积角度的主要因素有料浆屈服应力、黏度以及自流堆积速度,且从实验数据表2和表3可知,上述参数随着含砂率增大呈明显的变化趋势,对堆积角度产生较大影响。因此,必须对上述参数进行回归分析,才能减小堆积角度理论计算值与实测值误差。采用数据统计分析软件并结合料浆参数特性对实验数据进行回归分析,回归模型结果如式(2):
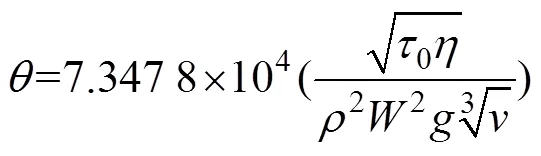
与Sofra & Boger公式相比,该公式对其中3个参数及系数进行了调整,并对回归分析公式的准确性进行了校验,结果见表5,图7为回归分析后的自流堆积公式理论计算值与实测值对比。
由表5和图7可知,回归分析后的自流堆积角度公式,理论计算值与实测值相差0~27.04%,平均误差仅为11.43%,具有较高的精确性。因此,以Sofra & Boger公式为基础,经回归分析后的自流堆积角度公式,对分析和计算浆液–风积沙双相介质材料的堆积角度具有一定的指导意义。

表5 回归分析后的自流堆积角度公式检验

图7 回归分析后理论值与实测值对比
4 结论
a. 通过自流堆积模型实验,发现料浆堆积角度随着含砂率的增大呈现指数性增大的变化趋势,且堆积角度在增加过程中存在明显的“拐弯区间”含砂率35%~53%,该值可作为生产中均匀投砂比例的一个控制参数。
b. 通过流变参数测试实验,得到了不同含砂率条件下的浆液–风积沙双相介质材料的流变参数屈服应力0和黏度。
c. 通过对Sofra & Boger公式的回归分析,建立了适合浆液–风积沙双相介质材料的自流堆积角度计算式。经误差分析显示,该式误差率仅为11.43%,可作为料浆堆积角度预测的依据。
请听作者语音介绍创新技术成果等信息,欢迎与作者进行交流

[1] 冀前辉. 废弃煤矿废弃物地下灌注技术可行性探讨[J]. 煤田地质与勘探,2014,42(4):69–76. JI Qianhui. Feasibility of waste backfilling in abandoned coal mine[J]. Coal Geology & Exploration,2014,42(4):69–76.
[2] 刘浪,辛杰,张波,等. 矿山功能性充填基础理论与应用探索[J]. 煤炭学报,2018,43(7):1811–1820. LIU Lang,XIN Jie,ZHANG Bo,et al. Basic theories and applied exploration of functional backfill in mines[J]. Journal of China Coal Society,2018,43(7):1811–1820.
[3] 童立元,刘松玉,邱钰,等. 高速公路下伏采空区问题国内外研究现状及进展[J]. 岩石力学与工程学报,2004,23(7):1198–1202. TONG Liyuan,LIU Songyu,QIU Yu,et al. Current research state of problems associated with mined-out regions under expressway and future development[J]. Chinese Journal of Rock Mechanics and Engineering,2004,23(7):1198 –1202.
[4] 刘鹏亮,张华兴,崔锋,等. 风积砂似膏体机械化充填保水采煤技术与实践[J]. 煤炭学报,2017,42(1):118–126. LIU Pengliang,ZHANG Huaxing,CUI Feng,et al. Technology and practice of mechanized backfill mining for water protection with aeolian sand paste-like[J]. Journal of China Coal Society,2017,42(1):118–126.
[5] 张鹏飞,赵同彬,傅知勇,等. 矸石充填采空区顶板沉降规律及矸石承载特性分析[J]. 煤炭科学技术,2018,46(11):50–56. ZHANG Pengfei,ZHAO Tongbin,FU Zhiyong,et al. Analysis on roof subsidence law and gangue load bearing characteristics in gangue filling goaf[J]. Coal Science and Technology,2018,46(11):50–56.
[6] 刘辉,何春桂,董增林,等. 高水材料充填技术在减小地表沉降中的应用[J]. 煤田地质与勘探,2010,38(6):54–57. LIU Hui,HE Chungui,DONG Zenglin,et al. Surface subsidence based on filling technology with materials of high water content[J]. Coal Geology & Exploration,2010,38(6):54–57.
[7] 邱华富,刘浪,孙伟博,等. 采空区充填体强度分布规律试验研究[J]. 中南大学学报(自然科学版),2018,49(10):2584–2592.QIU Huafu,LIU Lang,SUN Weibo,et al. Experimental study on strength distribution of backfill in goaf[J]. Journal of Central South University(Science and Technology),2018,49(10):2584–2592.
[8] 王新民. 基于深井开采的充填材料与管输系统的研究[D]. 长沙:中南大学,2006. WANG Xinming. A study of filling materials and pipeline transportation systems in deep mines[D]. Changsha:Central South University,2006.
[9] 赵才智. 煤矿新型膏体充填材料性能及其应用研究[D]. 徐州:中国矿业大学,2008. ZHAO Caizhi. Study on coal mine new paste filling material properties and its application[D]. Xuzhou:China University of Mining and Technology,2008.
[10] 白仲荣. 采空区内浆料堆积规律试验研究[D]. 北京:煤炭科学研究总院,2016. BAI Zhongrong. Experimental study on the law of slurry packing in goaf[D]. Beijing:China Coal Research Institute,2016.
[11] 陈安惠,陈寿根,张恒. 高速公路下伏采空区风积沙充填技术试验研究[J]. 岩土工程与地下工程,2013,33(1):57–59. CHEN Anhui,CHEN Shougen,ZHANG Heng,et al. Experimental study on filling technology of aeolian sand in mined-out area under expressway[J]. Geotechnical Engineering and Underground Engineering,2013,33(1):57–59.
[12] SOFRA F,BOGER D V. Slope prediction for thickened tailings and paste[C]//8thinternational conference tailings and mine waste. Colorado:Colorado National University,2000:20–31.
[13] FITTON T. Tailings beach slope prediction[D]. RMIT University,2007.
[14] KWAK M. Flow behavior of tailing paste for surface disposal[J]. Mineral Processing,2005:201–227.
[15] JEWELL R J,FOURIE A B. Paste and thickened tailings:A Guide[M]. Perth:Australian Centre for Geomechanics,2002.
[16] 王晓东. 风积砂质高浓度胶凝充填材料性能与粉煤灰掺量关系分析[J]. 工程地质学报,2016,24(1):78–86. WANG Xiaodong. Relationship between engineeringer formance and mix proportion of fly ash for cemented and high concentration backfill material with wind-blown sand as aggregate[J]. Journal of Engineering Geology,2016,24(1):78–86.
[17] 王晓东. 风积沙质胶结充填材料性能对水固比响应分析[J]. 煤田地质与勘探,2016,44(6):106–112. WANG Xiaodong. Influence of the performance of aeolian erinaceous cemented filling materials on response of water-solid ratio[J]. Coal Geology & Exploration,2016,44(6):106–112.
[18] 朱世彬,王晓东,许刚刚,等. 煤矿采空区充填高浓度胶结材料流变特性试验研究[J]. 煤炭科学技术,2017,45(11):69–73. ZHU Shibin,WANG Xiaodong,XU Ganggang,et al. Experimental study on rheological properties of high concentration cementing materials in coal mine goaf filling[J]. Coal Science and Technology,2017,45(11):69–73.
[19] ADDIS P C,CUNNINGHAM E J. Comparison of beaching slopes from two centrally discharging tailings storage facilities[C]//C. Loan. I.M. Artbuthout. Proceedings of the 13thinternational seminar on paste and thickened tailings. Canada,2010:255–264.
[20] 习泳,杨盛凯,尹升华. 膏体自流坡度经验公式的检验与回归[J]. 中国矿山工程,2013,42(1):19–22. XI Yong,YANG Shengkai,YIN Shenghua. Verification and regression of empirical formula of paste gravity slope[J]. China Mine Engineering,2013,42(1):19–22.
Stacking angle of slurry-aeolian sand dual-phase medium filling material
BAI Zhongrong
(Xi’an Research Institute Co. Ltd., China Coal Technology and Engineering Group Corp., Xi’an 710077, China)
Stacking angle is an important parameter to describe the spatial accumulation pattern of filling material in the goaf. It has important guiding significance for determining the drilling distance, optimizing the slurry configuration and adjusting the grouting process parameters. In order to grasp the variation law of stacking angle of slurry-aeolian sand dual-phase medium filling material, using self-flow stacking model experiment of tailings and rheological properties experiment, the mixing ratio of aeolian sand was taken as a variable to determine the slurry accumulation parameters and rheological parameters on different conditions of sand ratio. Based on this, Sofra & Boger formula was modified and the accumulation angle calculation formula suitable for slurry-aeolian sand dual-phase media filling material was established, which provided a new way for the quantitative evaluation of filling material stacking angle.
goaf; stacking angle; aeolian sand; model experiment; rheological properties
TD265.4
A
10.3969/j.issn.1001-1986.2020.03.004
1001-1986(2020)03-0024-05
2019-01-16;
2019-04-29
中煤科工集团西安研究院有限公司科技创新基金项目(2015XAYZD16)
Science and Technology InnovationFund Project of Xi’an Research Institute of CCTEG(2015XAYZD16)
白仲荣,1989年生,男,甘肃平川人,硕士,工程师,从事矿山地质灾害防治技术研究和服务工作. E-mail:baizhongrong@cctegxian.com
白仲荣. 浆液–风积沙双相介质充填材料堆积角度实验研究[J]. 煤田地质与勘探,2020,48(3):24–28.
BAI Zhongrong. Stacking angle of slurry-aeolian sand dual-phase medium filling material[J]. Coal Geology & Exploration,2020,48(3):24–28.
(责任编辑 周建军)
