路面激励对矿用货车驱动桥壳动态强度特性的影响

许亚军

重庆大学机械工程学院，重庆 400044

0 引言

驱动桥壳是矿用货车的重要承载部件。设计桥壳时，传统的强度计算方法主要以静载荷为基础，选择相应的断面尺寸和安全系数进行静强度计算。但是实际应用中，由于车辆工况多变，桥壳承受来自不同路面的交变载荷，有必要分析交变载荷对桥壳强度的影响。

目前，对驱动桥壳强度计算和失效的分析已有大量研究。高晶等[1]结合多体动力学和有限元分析方法预测不同等级虚拟路面下驱动桥壳的疲劳寿命，分析疲劳破坏产生的原因。朱茂桃等[2]通过静态有限元方法和测试技术对驱动桥壳的强度和刚度进行研究，指出驱动桥壳与半轴套管过渡处的应力最大。褚志刚等[3]运用有限元方法研究驱动桥壳静力学和动力学特性，表明动态应力是后桥壳在实际应用中破坏的真正原因，同时指出传统的静力学设计和分析方法不足以解决汽车后桥壳的动态强度问题，但采用的准静态分析方法无法获得桥壳整体的瞬态应力分布状态。郑燕萍等[4]利用有限元方法模拟汽车驱动桥壳垂直弯曲刚性试验、垂直弯曲强度试验和垂直弯曲疲劳试验，并通过试验对有限元分析结果进行验证。郑燕萍[5]通过有限元模态分析和瞬时动态分析，指出瞬态分析能全面反映桥壳上各点的位移和应力等动态响应。唐应时等[6-7]利用多体动力学和静态有限元方法，对后桥壳进行强度、刚度和模态分析，找出桥壳断裂的原因并改进设计，获得满意效果，但瞬时动态仿真分析只研究了汽车左右轮同时通过单一凸块路面的情况，没有考虑路面变化和车速变化对驱动桥壳动态载荷的影响。朱峥涛等[8]采用静态有限元分析方法分析不同厚度桥壳的弯曲刚度、垂直静强度和疲劳寿命。李亮等[9]在静强度计算的基础上对驱动桥壳和焊缝的疲劳寿命进行分析，指出焊缝位置在工作过程中容易出现撕裂。朱茂桃等[10]采用有限元方法和疲劳损伤理论计算驱动桥壳的疲劳寿命，结果显示主减速器后盖处的焊缝对疲劳寿命有很大影响。丛楠等[11]提出通过有限元虚拟台架试验方式获取删减载荷谱的试验与分析方法，表明该方法能准确反映桥壳损伤，大幅缩短台架试验时间。张黎华等[12]根据驱动桥壳静强度分析理论，利用有限元方法对半轴套管断裂处进行强度计算，并提出相应的改进措施。Topac等[13]利用有限元方法预测驱动桥壳的疲劳寿命，研究疲劳裂纹产生的位置和原因，并进行试验验证。张骄等[14]采用静态有限元分析方法对不同工况下重载货车驱动桥壳的静强度进行分析计算。王铁等[15]研究路面不平度对驱动桥壳动态载荷的影响，但集中参数法无法分析桥壳整体的应力分布。罗天洪等[16]、丁晓明等[17]、白玉成等[18]和马超凡等[19]采用有限元方法进行汽车后桥壳的结构轻量化设计。周军超等[20]和罗建斌等[21]采用响应面法进行驱动桥壳可靠性的优化。

上述研究大多采用静态分析方法或是准静态分析方法进行模拟计算，部分研究通过实际路面测试和台架试验考虑了动载荷的影响，但研究方法工作量大、耗费多、周期长。目前为止，少有对重型矿用自卸货车驱动桥壳动态强度的研究。

针对上述问题，考虑矿山路面凹坑和凸块表面冲击的影响，采用数学软件MATLAB构建基于正弦函数的矿山凹凸路面冲击力模型，并基于有限元软件ANSYS建立驱动桥壳动态分析有限元模型。运用显示动力学有限元分析软件LS-DYNA研究不同路面和不同车速工况下驱动桥壳的动态特性，并根据分析结果提出相应的结构优化设计方案，以期为驱动桥壳的动态结构强度设计提供依据。

1 建模

1.1 桥壳有限元模型

驱动桥壳有限元模型包括桥壳和半轴套管，选用四面体实体单元对桥壳和半轴套管进行单元离散，半轴套管与桥壳之间的接触摩擦采用库仑摩擦，采用ANSYS软件建立驱动桥壳有限元模型，驱动桥壳动态分析几何模型和有限元模型如图1所示(图1a)中单位为mm)，有限元模型单元数为281 650，节点数为68 514。图1b)中，A、B为半轴在桥壳上的支撑位置，C、D为弹簧座在桥壳上的安装位置。桥壳材料为ZG40Cr，弹性模量为215 GPa，泊松比为0.27，密度为7720 kg/m3，屈服强度为345 MPa，极限强度为630 MPa。半轴套管材料为40Cr，弹性模量为211 GPa，泊松比为0.277，密度为7830 kg/m3，屈服强度为785 MPa，极限强度为981 MPa。

a)几何模型 b)有限元模型

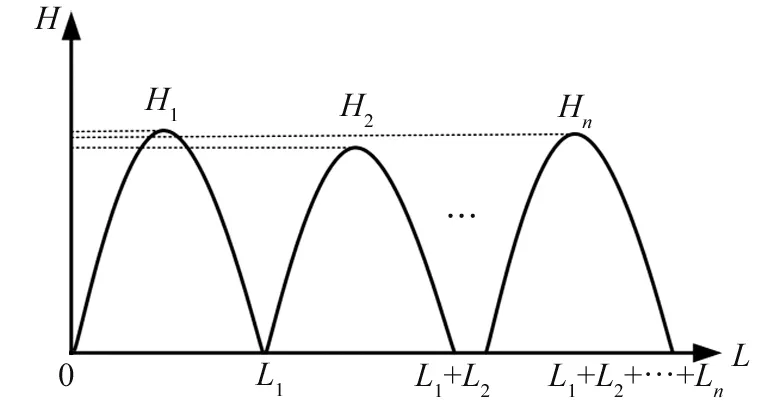
图2 路面激励函数示意图

1.2 路面激励模型

因矿山路面多为凹坑和凸起形态，实际路面激励非常复杂，且获取实际矿山路面载荷谱较为困难，为了描述不同路面不平度对驱动桥壳的动态激励过程，本文基于MATLAB软件将动态路面激励模型定义为正弦波形[16]的位移激励函数，如图2所示，该函数由半波长L和幅值H进行描述。当H为正值时，函数描述凸起路面的位移激励;H为负值时，函数描述凹坑路面的位移激励。

1.3 载荷与约束

驱动桥壳的设计载荷为245 kN。在图1b)C、D处分别施加122.5 kN载荷，路面激励函数施加在图1b)A、B处。约束A处表面节点x、z方向的平动自由度与B处表面节点z方向的平动自由度。

2 有限元分析理论

根据节点力平衡方程，单元的节点力与节点位移之间的表达式为：

Fd=KdSd，

(1)

式中：Fd、Kd、Sd分别为模型单元节点力向量、单元刚度矩阵和单元节点位移向量,Fd表示为:

(2)

式中矩阵元素Krs(r=i,j,m；s=i,j,m)表示为

(3)

式中：E和μ分别为模型材料弹性模量和泊松比；h为板厚；br、bs、cr、cs为待定系数，可由节点坐标计算得到。

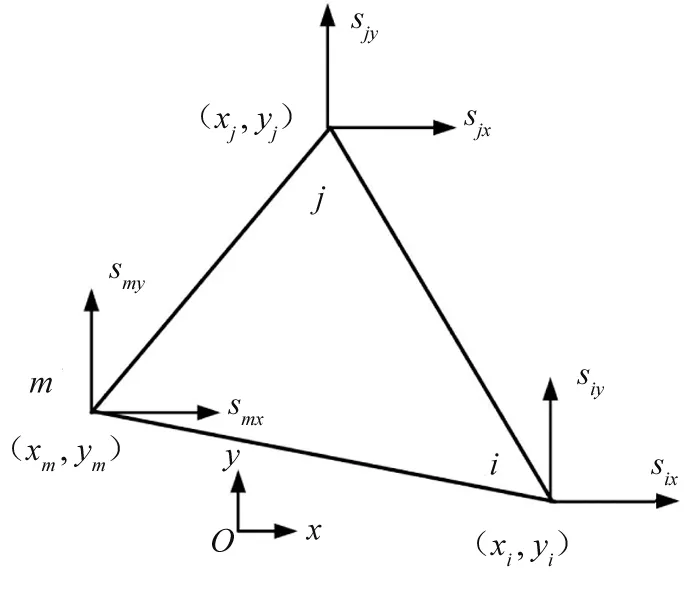
图3 三角形单元示意图

单元节点位移表示方法因单元形状和节点数不同存在差异。以图3所示三节点三角形单元为例，在平面直角坐标系xOy内，节点I、J和M的坐标分别表示为(xi,yi)、(xj,yj)和(xm,ym)，节点位移分别为six、siy、sjx、sjy和smx、smy，因此有

Sd=[sixsiysjxsjysmxsmy]，

单元的应变向量

ε=AεSd，

(4)

式中Aε为单元应变矩阵，表示为：

(5)

单元应力向量

σ=Dε

，

(6)

式中D为单元的弹性矩阵，表示为：

(7)

在驱动桥壳的有限元仿真分析过程中，已知单元的材料参数、单元形状、尺寸和节点坐标，由式(2)(3)获得Kd，由式(5)(7)得到Aε、D。已知节点所受外载荷Fd，综合考虑节点约束条件，由式(1)可求出Sd；将Aε、Sd带入式(4)可得ε；将D、ε代入式(6)可得σ。

3 驱动桥壳的静、动态特性仿真与结构优化

3.1 静强度仿真分析

为了寻找驱动桥壳的应力集中位置，基于式(1)～(5)的理论算法，首先在有限元分析软件ANSYS中对驱动桥壳的静强度特性进行仿真计算与分析。根据驱动桥壳的实际设计经验，取安全系数为2.0，驱动桥壳静强度有限元分析的应力分布云图如图4所示(图中单位为MPa)。由图4可知：驱动桥壳的最大应力集中在E、F附近的过渡圆角位置，且左右两侧的应力分布基本一致，左侧P1点的最大应力为167.990 MPa，右侧最大应力为165.070 MPa，该位置正是桥壳在实际使用过程中容易出现失效的位置，从一定程度上说明本文所建有限元模型的正确性。

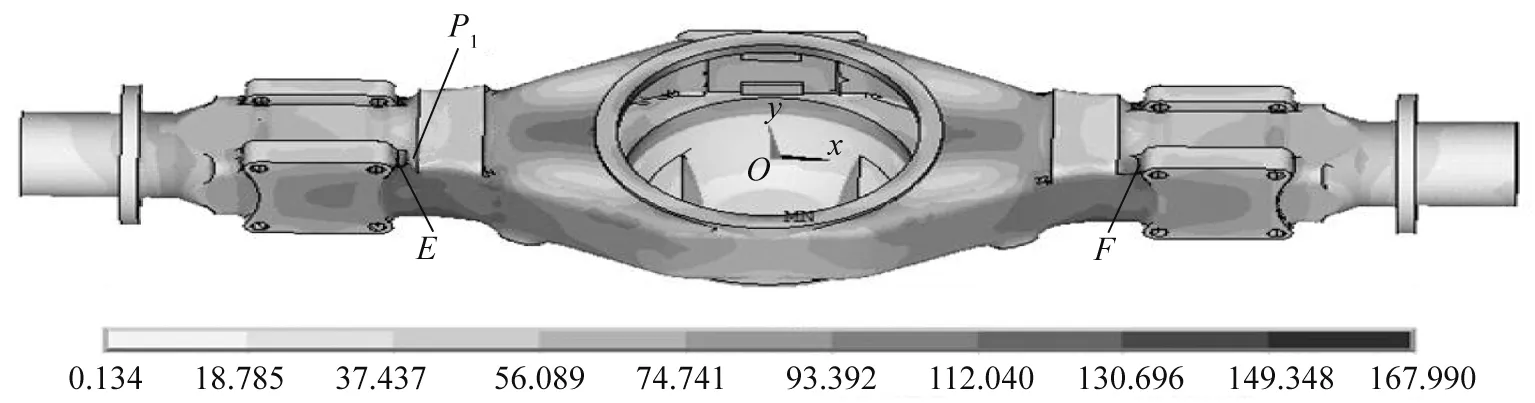
图4 静强度分析的等效应力分布云图

当安全系数为2.5、3.0时，采用相同的方法，得到P1点的应力分别为209.75、260.38 MPa。

3.2 动态特性仿真分析与结构优化

采用MATLAB软件编制对应车速下的路面激励谱(如图2所示)，将路面激励谱作为位移边界施加在图1b)的A、B处，载荷施加在图1b)C、D处。选取车速v=20 km/h，桥壳载荷为245 kN，采用LS-DYNA仿真分析不同L、H的正弦波形位移激励函数对驱动桥壳动态特性的影响；同时，保持桥壳的载荷不变，当L、H为定值时，仿真分析不同车速对驱动桥壳动态特性的影响。

3.2.1 不同路面对驱动桥壳动态特性的影响

保持选定的车速与载荷不变，L为1.0 m，H分别为0.10、0.15、0.20 m，分析不同路面激励H对驱动桥壳动态特性的影响。图5为驱动桥壳在通过凹凸路面激励过程中P1点的瞬时等效应力-时间历程曲线及其最大等效应力曲线。由图5a)可知：H不同时驱动桥壳的瞬时等效应力存在较大的波动，且其冲击变化的周期与凹凸路面的变化周期基本一致，说明路面的凹凸形态严重影响驱动桥壳的工作性能，凹凸路面导致的交变应力更可能导致驱动桥壳的危险位置出现疲劳失效。H越大，则瞬时等效应力越大。由图5b)可知：驱动桥壳的最大等效应力随着H的增加而增大，且远大于静强度分析获得的等效应力。

a)不同H时的瞬时等效应力时间历程曲线 b)最大等效应力随H的变化曲线

保持车速和载荷不变，选取H=0.20 m，L分别为1.0、1.5、2.0 m，计算不同路面激励L对驱动桥壳动态特性的影响。P1点的瞬时等效应力时间历程曲线及其最大等效应力曲线如图6所示。由图6a)可知：驱动桥壳通过不同L连续凹凸路面的瞬时等效应力存在较大波动，且其冲击变化的周期与凹凸路面的变化周期基本一致；波长较小的路面对驱动桥壳工作性能的影响较大，产生的交变应力更有可能导致驱动桥壳的危险位置出现疲劳失效。图6b)表明：随着路面激励L的增加，驱动桥壳的最大等效应力减小。同样，动态分析获得的等效应力远大于静强度分析的应力。

a)不同L时的瞬时等效应力时间历程曲线 b)最大等效应力随L的变化曲线

对比分析不同路面不平度激励下驱动桥壳的等效应力与静强度分析获得的应力可知：动态激励下驱动桥壳的等效应力远大于考虑不同安全系数的静强度分析的应力，表明传统的静态强度分析方法不能全面反映来自路面的动态激励载荷对驱动桥壳强度产生的影响，在驱动桥壳的设计过程中应充分考虑路面激励产生的动态载荷的影响，以保证其强度和寿命。

3.2.2 不同车速对驱动桥壳动态特性的影响

保持载荷不变，路面激励L=1.0 m，H=0.20 m时，选取车速v分别为10、15、20 km/h，讨论不同车速对驱动桥壳动态特性的影响。P1点的瞬时等效应力时间历程曲线及其最大等效应力曲线如图7所示。在通过连续凹凸路面过程中，图7a)中不同车速下驱动桥壳的瞬时等效应力存在较大的波动，且其冲击变化的周期与凹凸路面的变化周期基本一致。车速越大，对驱动桥壳工作性能的影响越大，过高的车速更可能导致驱动桥壳的危险位置出现疲劳失效。由图7b)可知：在相同的载荷和路面条件下，驱动桥壳的最大等效应力随着车速的增加而增大，且等效应力远大于静强度分析获得的应力。结果表明：在相同的路面激励作用下，不同车速产生的动态载荷对驱动桥壳的动态特性产生较大的影响，而传统的静态强度设计方法不足以解决这种动态载荷的问题。

a)不同v时的瞬时等效应力时间历程曲线 b)最大等效应力随v的变化曲线

3.2.3 结构优化

根据驱动桥壳的静、动态特性分析结果，驱动桥壳在如图4所示的P1位置存在应力集中现象。将该位置的圆角半径r由原始的1 mm优化为7 mm。仿真不同路面激励H和L以及v工况下，驱动桥壳优化后的最大等效应力如图8所示。由图8可以看出：增大应力集中位置的r可以有效降低驱动桥壳在该位置的最大应力，从而减小该处的变形。

a)H的影响 b)L的影响 c)v的影响

4 结论

本文对考虑不同安全系数的驱动桥壳的静强度特性和不同路面激励下桥壳的动态特性进行了仿真分析。

1)在路面动载荷的作用下，驱动桥壳产生的应力远大于静强度分析获得的应力，在设计驱动桥壳时，应充分考虑动态载荷对桥壳强度的影响，以保证驱动桥壳的强度和疲劳寿命。

2)驱动桥壳的动态应力随路面凸块高度和凹坑深度的增加而增大，随凸块和凹坑长度的增大而减小；在相同的路面激励作用下，驱动桥壳的动态应力随车速的增加而增大。

3)增加驱动桥壳应力集中位置的圆角半径，有利于减小该位置的应力集中现象。