基于WOA-BP的压力变送器温度补偿研究
2020-07-13马宏光曾国辉
马宏光,曾国辉,黄 勃
(上海工程技术大学电子电气工程学院,上海 201620)
0 引言
工业中,压力变送器主要用来监测压力参数,并将数据转换为标准工业电信号输出。在实际使用过程中,压力变送器的压力测量值会随着温度的改变而产生非线性误差,需要对其进行温度补偿。目前较为常用的补偿方式分为硬件补偿和软件补偿。硬件补偿缺点在于需要耗费额外的硬件成本,通用性差,补偿效果一般。而软件补偿方式较硬件补偿方式来说,补偿精度高,成本低,且有很强的可移植性。因此,本文主要研究软件补偿的方式,并提出一种鲸鱼算法优化BP神经网络的软件补偿方式。
1 压力变送器结构及原理
1.1 压力变送器结构
现有的压力变送器主要由以下几部分组成:单片机、温度传感器、压力传感器、模数/数模转换器、数据存储器等[1]。单片机通过A/D芯片接收温度传感器和压力传感器采集到的数据,经过程序运算处理后,由D/A芯片转换为标准的电信号,并通过通信装置发送到其他设备用于控制、存储等。图1为压力变送器结构框图。
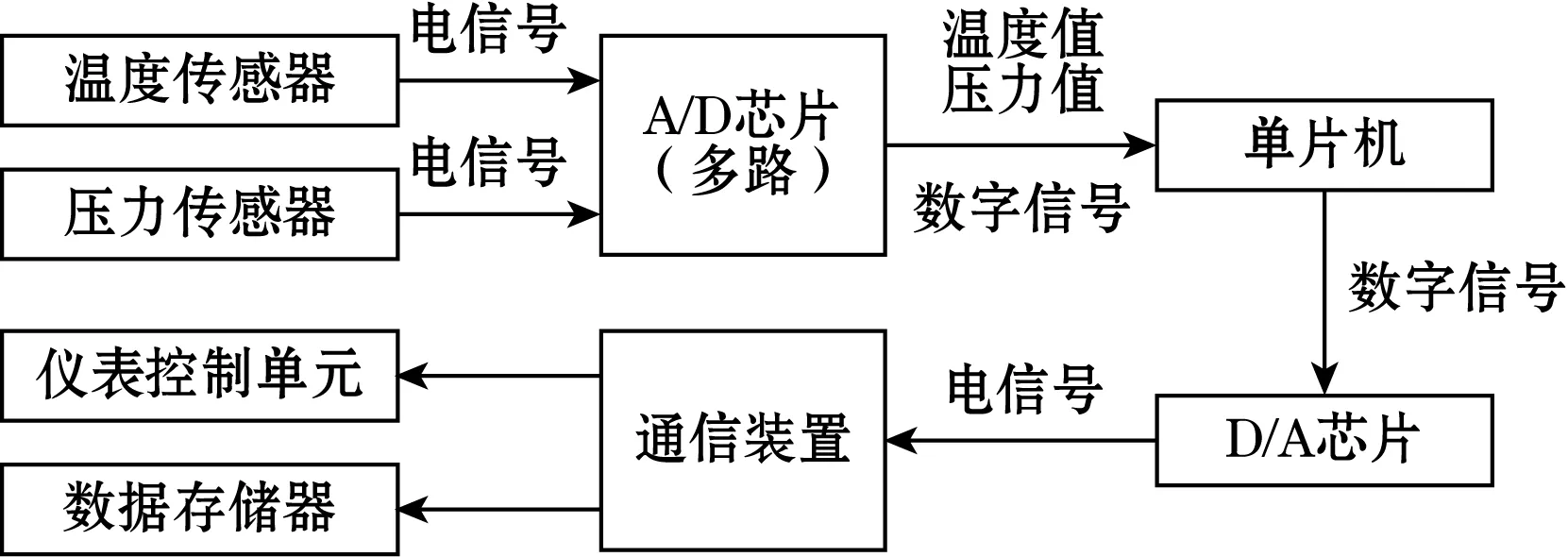
图1 压力变送器结构框图
1.2 压力测量原理
压力变送器常使用硅式半导体材料,利用“压阻效应”进行压力测量,即硅晶体的某一晶面压力改变时,晶体固有电阻率发生变化,从而使得惠斯登电桥平衡被打破,输出电压也随之改变,继而测得压力。图2为惠斯登电桥原理图[2]。由于半导体材料对温度变化灵敏度高,温度的变化将带来较大的非线性误差,为保证测量精度,需要对其进行温度补偿。
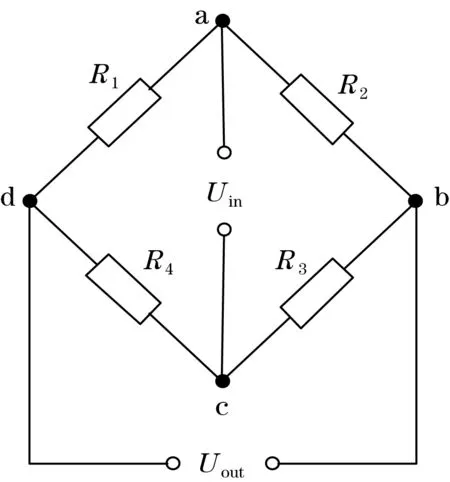
图2 惠斯登电桥原理图
2 基于WOA-BP的温度补偿模型
2.1 BP神经网络
由于BP神经网络具有较好的非线性映射能力,常用于温度补偿。文献[3]利用BP神经网络对压力变送器进行温度补偿,得到了良好的效果。图3为BP神经网络温度补偿的原理图。但BP神经网络存在收敛慢、迭代数多、易陷入局部最小和全局搜索能力不足等缺点[4]。文献[5]利用遗传算法优化BP神经网络,改善了整个网络的全局搜索能力,结果相比普通神经网络误差精度提高了一个级别,但收敛速度慢。文献[6]利用粒子群算法优化BP神经网络,解决了局部最小的问题,补偿后精度提高显著,但存在过早收敛的问题。
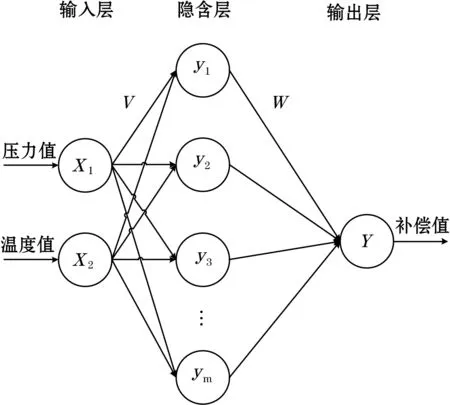
图3 BP神经网络温度补偿原理图
2.2 基于鲸鱼算法的BP神经网络
鲸鱼优化算法(whale optimization algorithm,WOA)是一种自然启发的元启发式优化算法[7]。通过模拟鲸鱼搜索、包围、捕食猎物的行为建立WOA数学模型,具体模型如下:
2.2.1 包围
D=|C·Xp(t)-X(t)|
(1)
式中:Xp(t)为最优个体的位置;X(t)为当前个体的位置;t为当前迭代数;C为对目标(猎物)的扰动;D为包围时的更新步长。
个体位置更新如式(2)所示:
X(t+1)=Xp(t)-A·D
(2)
随机变量A和C分别如式(3)和式(4)所示。
A=2a·r-a
(3)
C=2r
(4)
式中:r为[0,1]之间的随机数;a如式(5)所示,代表a从2线性减少到0;T为总的迭代次数。
a=2-2t/T
(5)
其中,A用于控制算法中鲸鱼群的扩充与包围。在|A|>1时,算法进行全局搜索,在|A|<1时,算法进行局部搜索。
2.2.2 捕食(泡泡网攻击)
鲸鱼捕食行为分为以下2种情况:
(1)收缩循环:通过迭代过程,将式(5)中a的值由2减为0,从而描述鲸鱼收缩包围食物的捕食行为。
(2)螺旋重新更新位置:在鲸鱼和目标位置间建立螺旋更新方程用于模拟鲸鱼的螺旋捕食运动,具体表示如式(6)和式(7)所示:
D′=|Xp(t)-X(t)|
(6)
X(t+1)=D′·ebl·cos(2πl)+Xp(t)
(7)
式中:b为螺旋形状的常数,一般设为l,l表示[-1,1]之间的随机数;D′为捕食时的更新步长,在捕食过程中,鲸鱼同时在以上2条路径上绕着猎物游动。
为了更新鲸鱼的位置,以上2种方法的概率均为50%。具体如式(8)所示:
(8)
2.2.3 搜索(勘查阶段)
该阶段鲸鱼进行游走觅食,使用随机选择个体的方案进行位置更新,从而提高了WOA算法的全局优化能力,使得鲸鱼算法具有了跳出局部最优解的能力。具体如式(9)和式(10)所示:
D″=|C·Xrand(t)-X(t)|
(9)
X(t+1)=Xrand(t)-A·D″
(10)
式中:Xrand为从种群中任意选取某一鲸鱼的位置;D″为探索时的更新与步长。
WOA算法在处理寻找最优解的过程中效率高、收敛速度快、精度高,并且调节参数少,具有跳出局部最优的能力[8-10]。因此提出WOA算法优化BP神经网络的温度补偿方法。具体流程如下:
(1)收集训练样本,归一化处理;
(2)算法初始化。设置迭代数、种群数,并将BP神经网络训练误差作为适应度函数;
(3)计算每个鲸鱼个体的适应度值,保存当前最优个体和位置;
(4)当t (5)当p<0.5时,若|A|<1,根据式(2)更新鲸鱼位置;若|A|≥1,根据式(10)随机更新鲸鱼位置; (6)当p≥0.5时,根据式(7)更新鲸鱼位置; (7)计算当前群体中最优个体,并保存个体位置。判断是否t>T,是则进入下一步;否则令t=t+1,重复执行(4)~(7)步; (8)输出最优鲸鱼位置,记录最优权值和阈值; (9)将优化的BP神经网络进行温度补偿,得出补偿后的结果。图4为WOA-BP算法流程图。 图4 WOA-BP算法流程图 实验中,压力变送器的传感器为Honeywell TSC系列硅压力传感器,量程为±10 kPa,实验温度范围为[20 ℃,55 ℃];实验压力范围为[0 kPa,10 kPa]。实验数据如表 1 所示。选用灵敏度温度系数αs和相对误差δ用于评价温度对传感器精度的影响程度[11]。其中,αs和δ分别表示为式(11)和式(12)。 (11) (12) 式中:ΔT为实验温度变化上下限差值量,即35 ℃;UPmax和UPmin分别为在相同压力下传感器输出的电压最大值和最小值。 表1 压力传感器实验数据 将AD码转换为电压值后,对比温度补偿前不同压力和温度状态下的传感器实际输出电压和测量输出电压,不同温度下电压与压力的关系曲线如图5所示。 图5 补偿前不同温度下电压-压力关系曲线 随温度改变,输出电压值与压力值会产生非线性误差,补偿前,灵敏度温度系数αs为1.32×10-3/℃,最大相对误差δ为4.6%。需要对其进行温度补偿。 利用MATLAB R2016b,对WOA-BP算法的温度补偿模型进行仿真,得到补偿后的压力值。其中迭代次数设置为100次,初始种群数为30。WOA-BP处理后的数据如表2所示。 表2 压力传感器补偿后数据 补偿后的灵敏度温度系数αs为4.01×10-4/℃,相对误差δ为0.48%。灵敏度温度系数提高了一个数量级,最大相对误差也从4.6%降到0.48%。补偿后不同温度下的电压-压力关系曲线如图6所示,可见提出的WOA-BP的温度补偿模型在压力变送器的温度补偿中是可行的。 图6 补偿后不同温度下的电压-压力关系曲线 为验证WOA-BP的优越性,将WOA-BP算法与现有的GA-BP神经网络、PSO-BP神经网络温度以及传统的BP神经网络补偿模型进行对比。不同温度补偿模型误差对比结果如表3所示。无论是灵敏度温度系数还是相对误差,WOA-BP的温度补偿模型较其他几种模型都有更好的效果。 表3 不同温度补偿模型误差对比结果 本文选用MSP430单片机作为核心处理器,将WOA算法训练好的BP神经网络固化进单片机中,再通过压力传感器的输出电压以及温度传感器的输出值经过AD7799芯片放大并转换后输入单片机内部,并进行数据融合处理后在液晶屏上显示。硬件电路结构框图如图7所示。 图7 硬件电路结构框图 本文提出基于WOA-BP神经网络温度补偿模型,利用WOA算法不易陷入局部最优、收敛速度快等特点得到了最优的BP神经网络权值和阈值,并用于压力变送器的温度补偿。补偿后的压力变送器测量系统的灵敏度温度系数为4.01×10-4/℃,最大相对误差为0.48%,满足实际应用需求。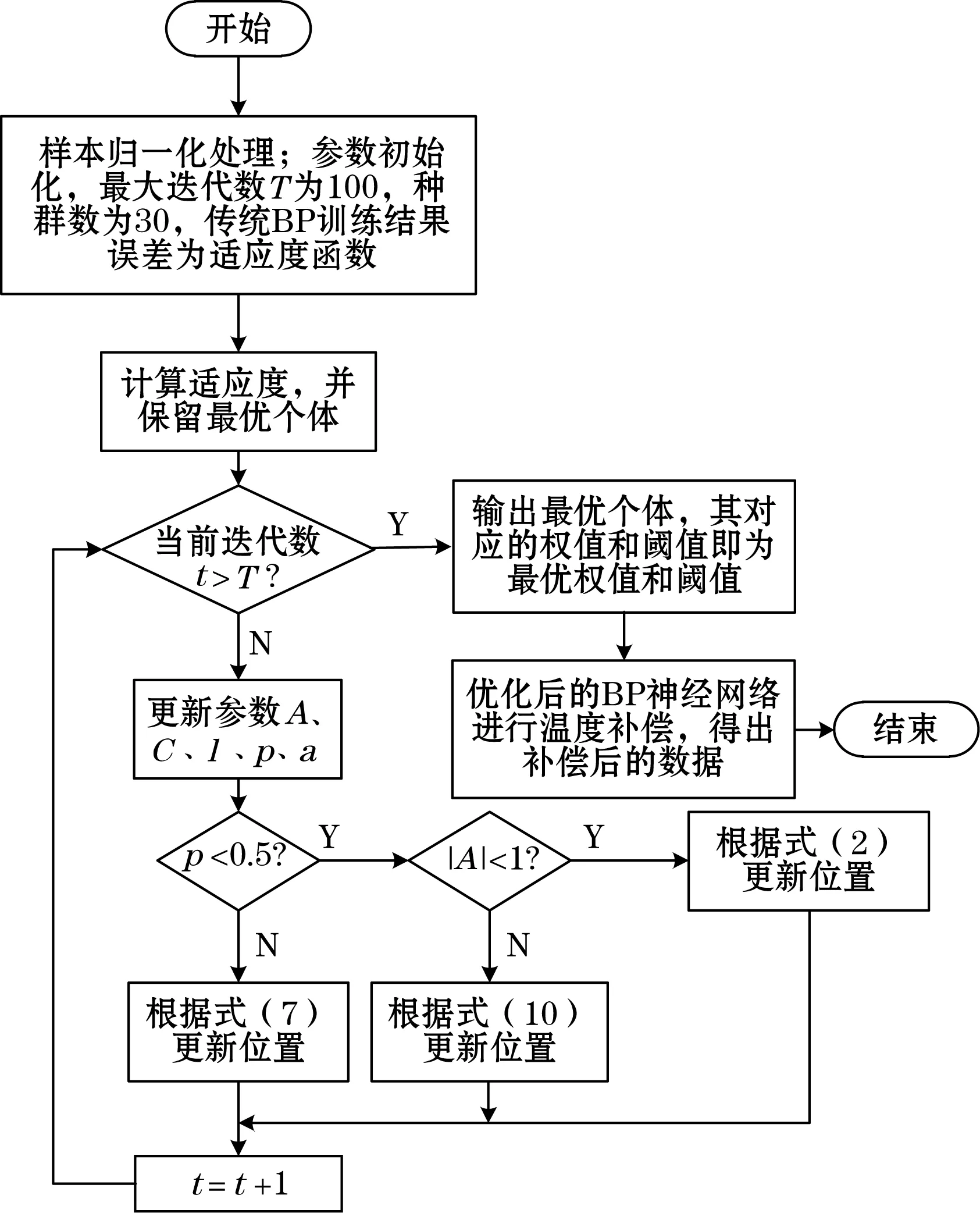
3 仿真与实验
3.1 软件仿真



3.2 硬件实现
4 结论
