不同冲击强度下的砂岩动态力学特性试验研究
2020-07-13万燎榕张宝骏
万燎榕,张宝骏
(1.江西省水利规划设计研究院,江西 南昌 330029; 2.中南大学资源与安全工程学院,湖南 长沙 410083)
在隧道、矿山等地下空间工程建设过程中,经常伴随着爆破、机械钻凿以及矿体震动等岩体活动发生[1-4],引起原岩应力场的重新分布,使得岩体处于一定的冲击荷载作用环境中[5-6],甚至导致岩体发生失稳、破坏。为达到减防灾的目的,对岩体中冲击波的传播以及岩石动态力学特性研究从未停止[7]。因此,通过研究不同冲击荷载对岩石破坏特性以及能量耗散规律的影响,对岩体爆破开挖时稳定性分析具有重要作用。
岩体开挖过程中,为达到预期的爆破开挖效果,在安全施工的同时如何提高破岩效率是岩土工程领域经常面对的难题,比如适当增加炸药量、提高机械钻凿强度等。然而,开挖强度的增强实则提高了输入冲击波的强度,这必然对岩体的稳定性、破坏程度等产生影响[8-10]。对此,许多学者采用不同的方式研究冲击强度对岩石力学特性的影响。FRIEDMAN等[11]利用液压伺服机及SHPB装置测试了花岗岩及石灰岩的动态力学性能。JANACH[12]通过试验证明了高应变率下花岗岩和石灰岩的抗压强度要远大于静载作用下抗压强度,并且破碎程度随应变率增加而提高。宫凤强等[13]研究表明,岩石的动态压缩强度随应变率的提高而提高,在应变率相同的情况下,岩石的动态压缩强度与弹性模量会随着围压的增大而增大,且岩石发生破坏的临界入射能,随着围压的增大而增大。LI等[14-15]对岩石在不同动静组合加载下的强度特性、破碎规律及吸能效率进行研究,冲击动载一定时,轴向静压从0增大到其单轴静压强度的70%时,岩石的组合加载强度大于其纯静载强度或纯动载强度。而随着冲击动载的增大,岩石的组合加载强度逐渐增大。然而,在岩体开挖过程中,能量耗散是岩体破坏的原动力,岩石变形破坏可以看成是不同形式能量之间相互转化结果,将产生不可逆的能量耗散[16]。因此,能量耗散反映了岩石内部微缺陷不断演化和强度不断弱化并最终丧失的过程[17]。冲击载荷作用下岩石力学特性是研究矿山开采、岩土爆破工程等的基础,国内学者对这方面已经开展了大量研究[18-20],希望通过分析能量耗散规律来对岩石变形破坏行为进行描述。尽管针对该方面的研究取得了一些成就,但主要集中于岩石静态或动态压缩性能方面,对于冲击载荷作用下岩石力学特性和能量耗散规律研究较少。
昌赣(南昌-赣州)高铁正积极建设中,江西省南部高山耸立,隧道开挖过程中最常见的就是砂岩,其均质性好且孔隙度较大[7]。在开挖过程中,其动态力学特性需要进一步研究。本文以改装的霍普金森压杆(SHPB)试验系统对砂岩进行了不同冲击强度的动力学试验,测得了砂岩的动态应力-应变曲线和应力波波形。基于此,分别对砂岩的动态应力-应变曲线特征、动态抗压强度、平均应变率、动态弹性模量等进行分析;同时,从砂岩破碎过程中的能量耗散角度分析了砂岩吸收能与冲击强度的关系。研究成果可以为地下隧道砂岩岩体的动态开挖提供理论参考。
1 试验材料及装置
1.1 砂岩试样
试验砂岩来自江西省赣南地区,此种砂岩均质性好且孔隙度较大,其粒径为0.06~2.00 mm,密度为2.50 g/cm3,孔隙度为5.32%,属于第三类砂岩[7]。经超声波测试,选用砂岩试样的波速介于2 200~3 500 m/s之间。荧光分光试验测试其矿物成分为二氧化硅,其含量大于75.88%。
根据国际岩石力学试验标准,使用岩石取芯机、切割机和磨石机对砂岩进行取样、切割和打磨,将其加工成尺寸为D×H=50.00 mm×50.00 mm,共20个试件,见表1。 试样两端面的平整度<0.05 mm,平行度<0.02 mm,以降低由于端面不平整而造成的试验误差。加工好的砂岩试样(图1(a))。另外,选取原岩体砂岩颗粒进行了显微电镜扫描试验(图1(b)),可以看出,砂岩中矿物颗粒大小一致、分布比较均匀。
1.2 试验装置
试验装置为中南大学研制的分离式霍普金森压杆(SHPB),该系统可实现加载静应力和动荷载的功能,如图2所示。该试验系统主要由动荷载加载装置、轴压加载装置、激光测速装置、数据采集和波形显示设备构成。 入射杆和透射杆的直径均为50 mm,长度分别为2 000 mm和500 mm。合金杆为40 Cr合金钢,其材料密度为7 810 kg/m3,弹性模量为250 GPa,纵波速度为5 410 m/s。动荷载加载装置主要由冲击杆、高压气室和发射腔组成。高压气室可为发射腔中的撞击杆提供冲击动能,然后撞击杆以一定速度冲击入射杆,进而对岩石试样输入冲击波(矩形波)。试验通过设置高压气室中的气压强度来实现撞击杆的冲击强度。

图1 砂岩试样及其电镜扫描图像Fig.1 Sandstone specimen and its scanning image by electron microscope
数据采集设备为中国北戴河实用电子技术研究所研制的SDY2016A超动态应变仪,超动态应变仪与应变片连接后可采集岩石中的冲击波信号,其测试应变系数为2.00 k,灵敏度为0.001 V/με。数据显示设备为日本Yokowaga公司生产的Yokowaga DL855E示波仪,该设备具有信号放大功能,显示时间间隔为1 μs,图像显示范围为-100~900 μs,精准度为0.005%,转化分辨率为12 bitA/D,测试范围为0.01~500 000 Hz。
2 试验原理及方案
2.1 测试原理
分离式霍普金森压杆(SHPB)试验是基于一级假设和均匀性假定的基础之上来完成应力波测试的。冲击杆输入的入射波在试样内经多次反射后,在试样和入射杆、透射杆处的应力应达到均匀,且忽略“试样-合金杆”界面处的摩擦效应。根据一维应力波理论,这里假设实测时刻t时砂岩中入射波、反射波及透射波对应的入射应力、反射应力和透射应力分别为σI(t)、σR(t)和σT(t),则砂岩中的平均应力可表示为式(1)[21]。

图2 改进式分离式霍普金森压杆示意图Fig.2 Diagram of improved Split Hopkinson Pressure Bar

(1)


(2)

(3)
根据砂岩-合金杆接触面的应力均匀性假定,则有式(4)。
σI(t)+σR(t)=σT(t)
(4)
于是,砂岩中的平均应力、应变和应变率可表示为式(5)~(7)。

(5)

(6)

(7)
式中:As和Ae分别为砂岩端部面积和入射杆、透射杆截面积,mm2;L为砂岩试样长度,mm;ρe为入射杆和透射杆密度,kg/m3;Ce为入射杆和透射杆弹性波波速,m/s。
2.2 应力波能量构成
若假设应力波能量用E表示,见式(8)。基于此,便可计算测试时间为t时的入射能WI(t)、反射能WR(t)、透射能WT(t)计算见式(9)。

(8)
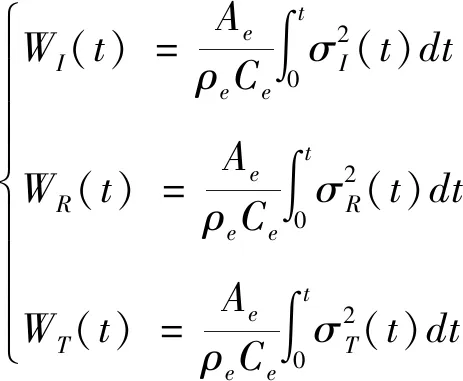
(9)
式中:Ae为入射杆和透射杆截面积,mm2;Ee为入射杆和透射杆弹性模量,GPa;ρeCe为弹性杆的波阻抗;t为应力波的延续时间,μs。
2.3 试验方案
试验过程中,将长径比≤1的砂岩试样放置于入射杆和透射杆中间,为保证应力波在“合金杆-砂岩”界面间良好传播,两界面处涂抹适量耦合剂(黄油)。当入射波被传送至“合金杆-砂岩”接触面处时,砂岩受到应力脉冲作用时发生塑性变形[22]。这时一部分入射波在界面处发生反射现象,形成与入射波方向相反的反射波,另一部分入射波被砂岩透射形成透射波。该过程形成的入射波、反射波可通过左侧应变片捕获,而形成的透射波可通过右侧应变片捕获。两应变片捕获的应力波由超动态应变仪转变为电信号,然后由瞬态波形储存器转换为离散信号存储起来,待试验完成后再进行分析和处理。按照试验方案,对加工好的砂岩试样进行不同冲击强度的应力波试验,具体试验步骤如下所述。
1) 将砂岩试样分五组,每组三个,分别编号为SY-2019-A1~SY-2019-A3、SY-2019-B1~SY-2019-B3、SY-2019-C1~SY-2019-C3、SY-2019-D1~SY-2019-D3、SY-2019-E1~SY-2019-E3。 按照试验方案(表1),冲击强度考虑了0.20 MPa、0.30 MPa、0.40 MPa、0.50 MPa、0.60 MPa五个等级,以冲击气压大小来表征对砂岩试样的冲击强度(p)。
2) 在入射杆和透射杆中间部位,纵向对称分别粘贴两个应变片,以降低试验误差。 将两应变片导线与超动态应变仪连接、超动态应变仪与示波器连接、示波器与计算机连接,同时检查信号传输是否正常。
3) 将砂岩试样加持于入射杆和透射杆中间部位,并保证三者中心处于同一水平线。为防止砂岩由于自重作用坠落,使用透明胶带固定。按照预定冲击强度,调试高压气室中气体强度,固定冲击杆在发射腔中的位置。
4) 发射冲击杆,冲击杆撞击入射杆后产生矩形波,应变片捕获应力波。应力波传输路径为:撞击杆→入射杆→砂岩试样→应变片→超动态应变仪→示波仪→计算机。然后,存储和处理试验数据。
3 试验结果与分析
3.1 动态应力-应变曲线分析
按照试验方案,对15个砂岩试样分别进行了0.20 MPa、0.30 MPa、0.40 MPa、0.50 MPa、0.60 MPa条件下的冲击破坏试验,测得了砂岩试样在冲击条件下的动态应力-应变曲线和应力波波形图。由于篇幅限制,图3中仅给出部分试验结果,图3(a)为不同冲击强度下试样的典型动态应力-应变曲线,图3(b)为砂岩冲击试验的典型应力波波形图。

图3 砂岩典型的动态应力-应变曲线与应力波形图Fig.3 Typical dynamic stress-strain curves and stress waveforms
由图3(a)可知,冲击荷载作用下的动态应力-应变曲线大致经历了“快速上升-平缓增加-随后下降”的发展趋势,并没有出现静态应力-应变曲线的压密阶段,而是直接进入近似弹性阶段,这与冲击的瞬态作用有关。砂岩在高速(激光测速仪测试结果表明,冲击速度介于3.48~10.96 m/s之间)、高强度的冲击作用下,短时间内砂岩中微裂隙来不及闭合而直接进入非线性塑性阶段[21,23],直到砂岩发生破坏。并且,砂岩冲击强度越大,动态应力-应变曲线就越快进入近似弹性阶段,其爬升斜率就越大。由表1可知,冲击强度由0.20 MPa增加到0.60 MPa,砂岩动态弹性模量介于5.81~18.41 GPa之间,增加了12.60 GPa。另外,同一冲击强度下的弹性模量相差较小,表明了试验材料的物理学特性(如孔隙度)具有一致性。
根据测试结果,提取了不同冲击强度下砂岩的动态抗压强度、破坏应变、平均应变率以及动态弹性模量等四个典型力学特征值,统计破坏形式(表1)。由表1可知,冲击强度为0.20 MPa时,个别砂岩出现破裂现象(破坏程度亚于破碎),而随着冲击强度增加,砂岩破坏形式均为破碎状态。由此可见,岩体开挖过程中,适当提高冲击强度可以有效提高破岩效果。

表1 不同冲击强度下砂岩力学特征值Table 1 Mechanical characteristics values of sandstone under different impact strength
砂岩动态应力-应变曲线变化路径表明,冲击强度越大,砂岩应力-应变曲线变化路径越长,破坏时的动态抗压强度越大,对应的破坏应变越大。由表1可知,随着冲击强度增加,砂岩动态抗压强度介于8.95~60.01 MPa之间,增加了51.06 MPa;破坏应变介于0.002 088~0.010 690之间,增加了0.001 069;平均应变率介于55.89~110.14 s-1之间,增加了54.25 s-1。这说明,增加的冲击强度不仅提高了砂岩的破碎程度而且提高了砂岩对外力的抗冲击能力,这与研究结论[13,15,23]一致。此外,通过对煤岩的动态力学特性研究,王登科等[22]将动态应力-应变曲线划分为线弹性阶段、弹塑性阶段和塑性软化阶段,当应力上升到动态抗压强度的80%时,应力-应变曲线的上升趋势开始减缓,随后岩样破坏,曲线总体开始下降,这与上述结论一致。
3.2 砂岩的动态抗压强度特征
由图3(a)和表1可知,不同冲击强度作用对砂岩动态抗压强度变化具有显著性差异,随着冲击强度和平均应变率的增加,砂岩动态抗压强度显著提高,谢晓锋等[21]称该现象为应变率效应。随着冲击强度增加,砂岩动态抗压强度在8.95~60.01 MPa范围内增长式变化。冲击强度由0.20 MPa增加到0.60 MPa时,平均动态抗压强度增加了521.22%,随着冲击强度的增长速率为123.18 MPa/MPa。
图4给出了砂岩平均动态抗压强度(σv)随冲击强度(p)增加的变化趋势。由图4可知,随着冲击强度增加,砂岩平均动态抗压强度呈线性增加,这也表明,尽管冲击强度提高了岩石的破碎效果,但增加的冲击强度同时也提高了岩石对外界扰动的抵抗力。拟合分析发现,平均动态抗压强度随冲击强度增加呈一次线性函数变化,相关系数R2=0.987。
另外,由表1可知,随着冲击强度增加,砂岩动态抗压强度呈现增大的同时,其破坏时对应的破坏应变也呈规律性变化。 图5为砂岩平均破坏应变(εfv)与冲击强度(p)的关系。结合图5和表1可知,随着冲击强度增加,砂岩破坏应变值介于0.208 8~1.069之间,其平均值由0.271 6×10-2增加到0.978 9×10-2,随着冲击强度的增长速率为0.117 9×10-3MPa-1。由图5可知,尽管部分平均破坏应变值离散性较大,但总体随着冲击强度增加呈线性函数增加,其相关系数R2=0.921,拟合函数如图5所示。

图4 平均动态抗压强度与冲击强度的关系Fig.4 Relationship of average dynamic compressive strength and impact strength

图5 平均破坏应变与冲击强度的关系Fig.5 Relationship of average failure strain and impact strength
3.3 砂岩的应变特征
由图3(a)可知,冲击荷载作用下的砂岩动态应力-应变曲线表现出显著的弹性阶段,这与冲击作用下的瞬态应变效应有关。分析认为,当对砂岩试样施加瞬态的冲击应力时,其内部原生裂隙在极短时间内无法完成压缩、变形[18],在抵抗外力作用时依然保持敞开状态。这就导致砂岩直接产生弹性变形,进入弹性变形阶段,进而引起动态破坏的极限强度相比静态有所增加,同时,砂岩破坏时的应变也显著提高。
图6给出了砂岩平均应变率随冲击强度增加的变化规律,很显然砂岩的砂岩平均应变率是随着冲击强度的增加而增加。当冲击强度由0.20 MPa增加到0.60 MPa时,砂岩平均应变率由60.87 s-1增加到101.90 s-1,相对增加了67.41%。拟合发现,砂岩平均应变率随着冲击强度增加符合一阶指数函数增长,其相关系数R2=0.901。
另外,有研究表明[19,24-25],岩石的动态抗压强度随着应变率的增加不会无限制的增加,当应变率达到某一数值时,动态抗压强度会出现降低趋势。图7给出了砂岩平均动态弹性模量、动态抗压强度随平均应变率增加的变化关系。由图7可知,平均应变率处于前三个数据时(60.88~66.79 s-1),砂岩动态抗压强度表现出快速增加,而随着平均应变率继续增加(66.79~101.90 s-1),其动态抗压强度增加幅度减缓。但总体来讲,砂岩动态抗压强度随平均应变率增加近似为线性增加,相关系数R2=0.887。从图7还可以看出,砂岩平均动态弹性模量与平均应变率呈线性函数关系(R2=0.979),这与文献[22]结果一致。

图6 平均应变率与冲击强度的关系Fig.6 Relationship of average strain rate and impact strength

图7 平均动态弹性模量、动态抗压强度与平均应变率关系Fig.7 Relationship of average elastic modulus, compressive strength and average strain rate
3.4 砂岩能量耗散规律
3.4.1 能量构成与分布特征
由式(9)可计算出不同冲击强度下砂岩的能量构成与分布情况,基于此,图8(a)给出了入射能、反射能、透射能(这里均指平均能量)随着冲击强度增加的变化趋势。
由图8(a)可知,随着冲击强度增加,入射能、反射能和透射能呈不同程度的增加,入射能和反射能明显大于透射能。由计算结果可知,当冲击强度由0.20 MPa增加到0.60 MPa时,入射能由53.28 J提高到282.23 J,反射能由29.85 J提高到184.71 J,而透射能仅从1.62 J提高到2.34 J。
由图8(a)还可以看出,入射能和反射能随冲击强度增加的变化趋势具有一致性,而透射能的增长趋势不是很明显。总体来讲,入射能、反射能、透射能随冲击强度增加呈非线性增加,拟合表明两者具有较好的一节指数函数关系,其拟合方程及拟合参数,见表2。表2中,E为入射能、反射能和透射能,J;E0、E1为拟合参数,J;α可表征拟合方程增长快慢程度,MPa-1;R2为拟合相关系数。

图8 应力波能量构成及透反射系数Fig.8 Energy composition and reflection coefficient, reflection coefficient of stress wave

表2 拟合方程及拟合参数Table 2 Fitting equation and corresponded parameters
为观察砂岩冲击强度对应力波的透射系数和反射系数的影响程度,可通过式(10)和式(11)计算,应力波的透射系数和反射系数随冲击强度增加的变化趋势如图8(b)所示。由图8(b)可知,当冲击强度小于0.40 MPa时,透射系数和反射系数变化程度比较明显;当冲击强度大于0.40 MPa时,透射系数和反射系数开始逐渐趋于稳定。这表明,透射波和反射波对较小冲击强度较为敏感,而随着冲击强度增加,这种敏感性逐渐降低。 回归分析发现,随冲击强度增加,透射系数和反射系数分别呈幂函数和对数函数变化,相关系数分别为R2=0.881和R2=0.983。

(10)

(11)
3.4.2 砂岩吸收能变化规律
在不考虑弹性杆和砂岩接触面处能量损失的情况下,假设冲击杆输入的能量完全转化为入射能,则可知不同冲击强度下能量由入射能、透射能、反射能和试样吸收能构成。根据能量守恒定律,砂岩的吸收能(指平均吸收能)可表示为式(12)。

(12)
基于式(12),图9给出了砂岩吸收能随冲击强度的变化规律。由图9可知,随着冲击强度增加,砂岩试样的吸收能呈指数函数逐渐增加,增长系数为3.77,相关系数R2=0.92。这表明,由于随着砂岩试件吸收能量不断增加,试件中能量传递速率加快。从砂岩的破坏形式来看(表1),在较低冲击强度下,砂岩试样的动态冲击破坏呈出现了局部劈裂破坏,且破碎程度较小、碎块均匀度相差较大;而当冲击强度较大时,砂岩试样均呈现压碎破坏,其碎块较小、均匀度较好。
由图9可知,产生上述现象的主要原因是冲击强度增加时,砂岩瞬间产生的应变率就越大,吸收能会随输入能的增大而进一步增加,进而用于破坏砂岩的能量就越多。最终,砂岩试件中裂纹扩展程度以及损伤的累积量加剧,从而导致砂岩的破坏越彻底。图10还表征了砂岩平均动态抗压强度与吸收能的变化关系,砂岩吸收能与平均动态抗压强度之间呈正相关。回归分析发现,砂岩平均动态抗压强度与吸收能呈对数函数变化,相关系数R2=0.920。
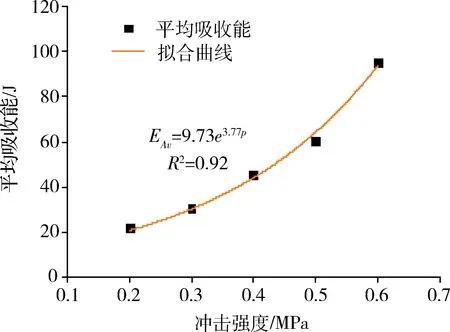
图9 吸收能与冲击强度的关系Fig.9 Relationship of absorption energy and impact strength

图10 平均动态抗压强度与吸收能的关系Fig.10 Relationship of average compressive strength and absorption energy
4 结 论
1) 砂岩动态应力-应变曲线大致经历了“快速上升-平缓增加-随后下降”的发展趋势,未出现压密阶段直接进入近似弹性阶段,这与冲击的瞬态作用有关。冲击强度越大,应力-应变路径越长。
2) 冲击强度对砂岩动态强度和应变特征具有显著性影响,随着冲击强度和平均应变率增加,动态抗压强度显著提高。平均动态抗压强度和平均破坏应变随冲击强度增加呈线性增长规律,而平均应变率与冲击强度符合一节指数函数增长;平均动态抗压强度和平均动态弹性模量均随平均应变率增加呈线性函数增加。
3) 随着冲击强度增加,入射能、反射能和透射能均呈不同强度的指数函数增加,入射能和反射能明显大于透射能。透射系数和反射系数与冲击强度分别呈幂函数和对数变化。增加的冲击强度提高了砂岩吸收能,加快了能量传递速率,吸收能随冲击强度增加呈指数增长。
致谢感谢东华理工大学的武为博士对本文理论部分的指导。
