基于Fisher-逐步判别法的煤与瓦斯突出预测

李长兴，辛程鹏，李回贵，刘义磊

(1.贵州工程应用技术学院矿业工程学院，贵州 毕节 551700； 2.中国矿业大学(北京)应急管理与安全工程学院，北京 100083)

煤与瓦斯突出是在地应力和瓦斯的共同作用下突然从煤体或岩体内向巷道和采掘空间抛出大量煤岩和瓦斯的异常动力现象，具有极强的破坏性，给煤炭企业造成了巨大的经济损失和人员伤亡[1]。随着我国煤矿机械化开采水平的提高和采掘深度的延深，煤与瓦斯突出现象日趋更加严重[2]。近年来，国内外学者对煤与瓦斯突出预测做了大量的研究工作，提出了多种有效的预测方法，这些方法极大地推动了煤与瓦斯突出预测研究工作的快速发展，如综合指标法、神经网络法、电磁辐射法、灰色理论法、免疫遗传法、可拓聚类法等[3-8]。由于煤与瓦斯突出极其复杂，突出预测的敏感指标和临界值很难确定，目前对突出发生的机理也尚不能完全掌握，因此，如何对煤与瓦斯突出准确无误地进行预测预报成为了煤矿安全开采中的关键一环。笔者基于数理统计分析理论，利用逐步判别法对影响煤与瓦斯突出的指标进行筛选，建立煤与瓦斯突出的Fisher判别分析模型。从杂乱无章的突出实例数据中来寻求它们之间的内在联系，用直观的数学方法来反映总体间的差异性，以寻求一种能够判定新样本总体类别归属问题的最优方法，从而有效地对煤与瓦斯突出危险性进行判别预测。

1 Fisher判别分析法

1.1 Fisher判别法基本原理

Fisher判别法的基本思想就是将高维特征向量空间投影到低维空间。该方法的基本思路就是将n维空间中的某一个点x=(x1,x2,x3,…,xn)转换为一维函数y(x)：y(x)=∑Cjxj,然后利用该一维函数把n维空间中的所有已知类别总体和求知类别归属的样本数据都转换成一维数据，再根据样本数据点之间的亲疏程度来判定未知样本数据点的归属类别。通过降维，根据组间距离最大、组内距离最小的原则确定的判别分析函数不仅能将新的样本进行判别分类，而且能获取非常高的判别效率。

1.2 Fisher判别函数与判别准则

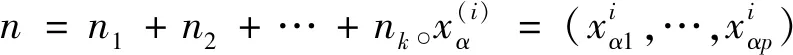
ei=E(y|Gi)=a′μ(i)，i=1，2，…，k

(1)

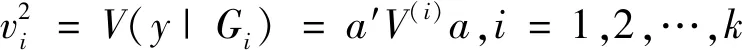
(2)

令：

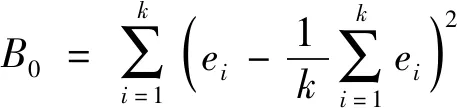
(3)

(4)

B0相当于一元方差分析中的组间差，E0相当于组内差。令μ′为式(5)。

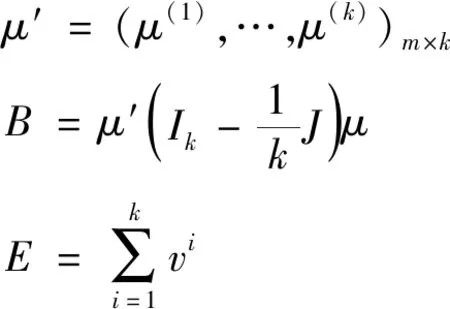
(5)

则可得Δ(a)=B/E=a′Ba/a′Ea。很显然，B,E均为非负定阵，Δ(a)的极大值为方程|B-λE|=0的最大特征根，取a为对应于λ1的特征向量即为判别函数的系数，即可求出判别函数。由数学知识可知，特征根的个数m是不会超过min(k-1,p)个的，由此可构造出m个判别函数，为式(6)。

yl(x) =c(l)Tx,l= 1,2,…,m

(6)

对于每一个判别函数必须要用一个指标pi来其衡量判别能力，其中pi可定义为式(7)。

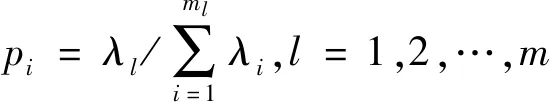
(7)

m0个判别函数y1,y2,…,ym0的判别能力定义为式(8)。

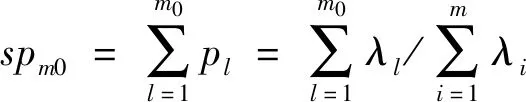
(8)

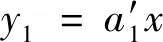
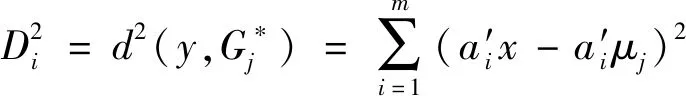
(9)

j=1，2，…，k。由此可得判别规则，见式(10)。

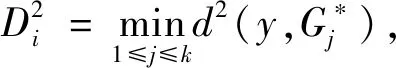
(10)

2 煤与瓦斯突出预测的Fisher-逐步判别模型

2.1 判别因子逐步判别筛选过程

在判别分析问题中，影响判别能力的变量很多，且影响程度大小不一。如果把主要变量误剔除，那么建立的判别函数其判别效果一定不佳；但判别变量很多而又不加剔除地全部被选入会造成在求解逆矩阵时计算精度下降。选取国内典型突出矿区的30个突出实例(收集自不同矿井的同一组煤层，且工程地质条件类似)，其中20个作为训练样本(表1)，另外10个作为待判样本(表5)。采用逐步判别分析法[11]对影响煤与瓦斯突出的敏感指标进行逐步判别筛选，由于收集到的突出实例中常用的敏感指标最大钻屑量Smax、钻屑解吸指标K1和Δh2等数据缺失，故采用其他5个敏感指标(即瓦斯压力、放散初速度、坚固性系数、煤体破坏类型和埋藏深度，分别用x1、x2、x3、x4、x5表示)进行逐步判别筛选，其中煤体破坏类型分为5类：1(非破坏煤)、2(破坏煤)、3(强烈破坏煤)、4(粉碎煤)、5(全粉煤)。取F进=5.0，F出=3.5作为逐步判别停止的临界值。若某一变量F≥5.0时，则表明该变量判别能力显著，需将其加入到判别模型中；若某一变量F≤3.5时，则表明该变量判别能力微弱，应将其剔除出判别模型。重复以上过程，直至计算到既没有变量加入也无变量被剔除，逐步判别分析过程才算结束。由于篇幅所限，对于逐步判别筛选判别因子的具体步骤不再详述。最终从给定的5个评价指标中将坚固性系数x3、煤体破坏类型x4剔除出突出判别函数，将瓦斯压力x1、瓦斯放散初速度x2、埋藏深度x5选入作为突出判别因子。

表1 样本数据及分类结果Table 1 Sample data and discriminant results

根据多元统计方差分析原理，定义A为样本数据点的组内离差平方和，T为样本数据点的总离差平方和，此时有：Λ=|A|/|T|,要对某一变量的判别能力的显著性进行分析，可按下面步骤来操作。

判别函数中假设已有q个变量，记X*,若考虑是否有必要添加变量Xj,可通过计算偏威尔克斯统计量，见式(11)。

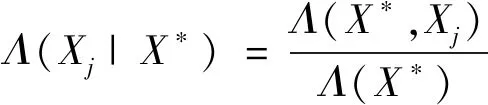
(11)

式中,Λ(X*，Xj)为X*与Xj的威尔克斯统计量。可以证明，见式(12)。

Fα(k-1,n-k-q)

(12)

即F进=Fα(k-1,n-k-q),如果有F≥F进,则表明变量Xj判别能力显著，在判别函数中相应地有必要增加变量Xj。针对判别函数中已有的q个变量X*,如若存在有对判别能力不显著的变量，则需将其剔除出判别函数。如考虑变量Xk是否可从判别函数中剔除，记剔除Xk的变量组为X*(k),则有式(13)。

Fα(k-1，n-k-q+1)

(13)

此时，若有F≤Fα(k-1,n-k-q+1)=F出,则说明变量Xk的判别能力不显著，需要把Xk从X*中剔除掉。重复以上引入和剔除变量的过程，直到既不能将新变量引入，又不能把已选入判别函数的变量剔除掉为止，至此便可用已选入的变量来构建判别分析函数。

根据以上计算公式，取F进=5.0，F出=3.5作为逐步判别停止的临界值。重复以上过程，直至计算到既没有变量加入也无变量被剔除，逐步判别分析过程才算结束。由于篇幅所限，对于逐步判别筛选判别因子的具体步骤不再详述。最终从给定的5个评价指标中将坚固性系数x3、煤体破坏类型x4剔除出突出判别函数，将瓦斯压力x1、瓦斯放散初速度x2、埋藏深度x5选入作为突出判别因子。

2.2 Fisher判别分析模型的建立

《防治煤与瓦斯突出规定》指出[12]，在进行煤与瓦斯突出危险性鉴定时，给出的矿井鉴定结果是否为突出矿井，而对突出矿井的突出类别大小没有给出。研究表明[13]，对于有些矿井其各项突出指标值并没有超过其临界值，但也有可能会发生煤与瓦斯突出；根据突出时抛出煤的重量不同将突出分为4类：Ⅰ-无突出、Ⅱ-小型突出(50 t以下)、Ⅲ-中型突出(50～100 t)、Ⅳ-大型突出(100 t以上)。根据上面所述建模过程，将表1中所列出的20组煤与瓦斯突出实例作为学习训练样本建立Fisher判别模型，经训练学习并计算可得到表2中各个Fisher判别函数的系数，因此建立的判别函数分别为：y1=2.217x1+0.151x2-0.007x5-2.578；y2=0.551x1-0.19x2+0.012x5-5.894；y3=-0.4x1+0.266x2+0.004x5-3.661。

表3为各判别函数特征值及组质中心值。从表3中给出的方差百分比可知：第1个判别函数方差的贡献率为77.2%，说明此函数可以解译77.2%的样品信息，利用该函数能够对绝大部分样品类属进行判别；第2个判别函数方差的贡献率为14.4%，说明该函数可以解译14.4%的样品信息；第3个判别函数方差贡献率为8.4%。当利用第1个判别函数对样本属类无法作出明确判断时，可分别依次使用第2个判别函数和第3个判别函数来对样本分属类别进行判断。从3个判别函数的累积方差贡献率为100%可知，当把3个判别函数联合起来使用时，可以完成对所有样品分属类别的判断。

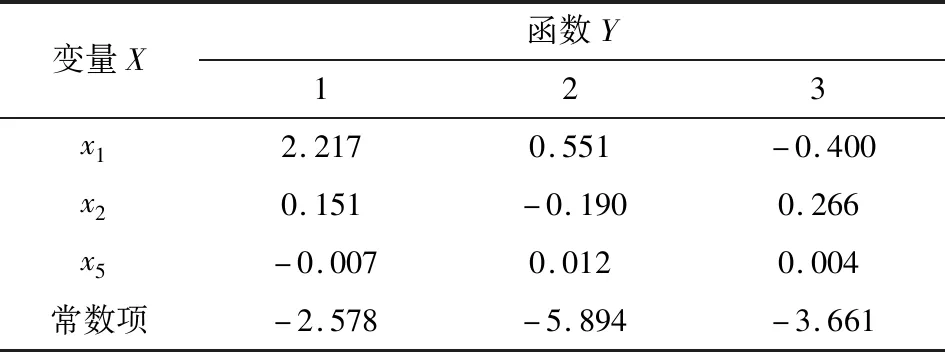
表2 Fisher判别式函数系数Table 2 Coefficient of Fisher discriminant function

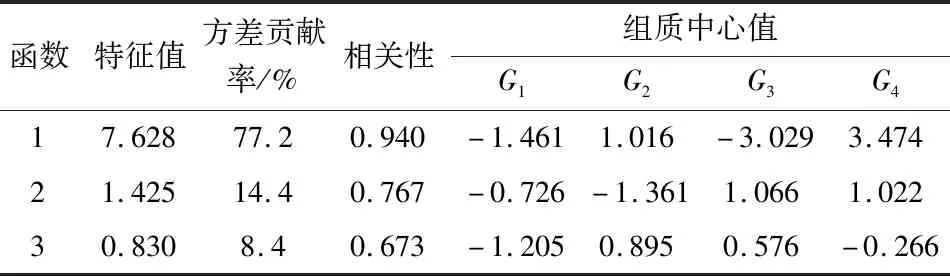
表3 判别函数方差贡献率及组中心值Table 3 Discriminant function variance contribution rate and group center value

2.3 Fisher判别效果显著性检验

为了考察上述所求判别函数的准确度，可采用计算其误判率的检验方法。通常采用以样本数据回代估计的方法来计算误判率，即把所有训练样本重新作为新样本代入构建的判别函数中，根据判别准则对其类别归属进行判别，并用被误判的样本个数与所有训练样本个数的比值来代表误判率，误判率越低表明建立的模型判别效果越好。对20组训练样本进行回代估计检验，其回判结果见表4。图1是利用第1判别函数和第2判别函数对样本进行类别分组的示意图，从图中可清晰地看出，绝大部分样本都集中在各自所属类别的组中心值附近，组均值和组间离差大，组内离差较小，20组样本的聚合程度及分离效果均非常明显。

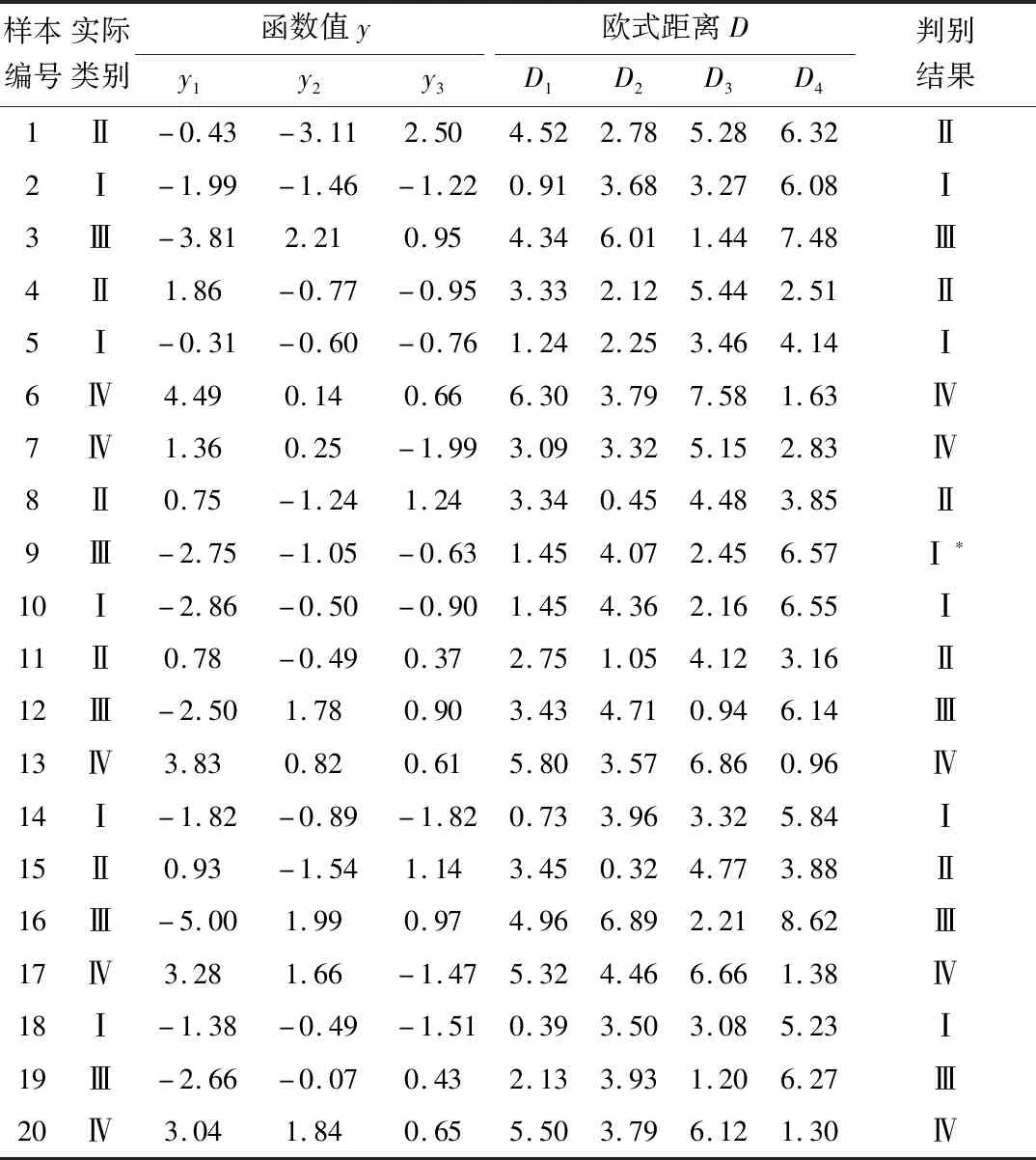
表4 样本数据及分类结果Table 4 Sample data and discriminant results

注：“*”为误判样本

从表4中给出的判别结果可知，20个突出训练样本回判后只有1个训练样本出现判别结果与实际不相符的情况，其误判率仅为5.0%。出现判别错误的样本为编号9，它的实际突出类别为Ⅲ，结果利用所建立的判别函数将其突出类型判为Ⅰ。出现这种误判的情况，可能跟数据采集点的地质条件和人的因素有关。另外，从图1也可清楚地看出，编号9的样本处在突出类别Ⅰ和类别Ⅲ的交界处，很容易引起误判。因此，在实际突出判别应用时，需密切结合突出地点的地质条件，以保证煤与瓦斯突出判别的准确性。从误判率可见，Fisher-逐步判别分析方法能够有效地对煤与瓦斯突出进行判别预测，而且方法简单可靠，准确率高。

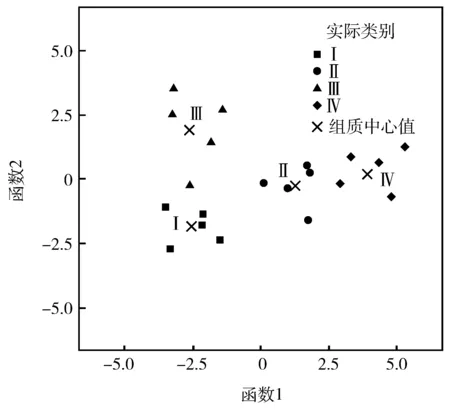
图1 第1判别函数和第2判别函数分组Fig.1 Groups of the first and second discriminant function

3 工程应用与分析

利用建立好的Fisher判别分析模型对选取的另外10个突出实例进行突出危险性判识，见表5。将各实例的判别因子数值逐一分别代入第1判别函数、第2判别函数和第3判别函数，得到3个判别函数值，得到的3个函数值形成的是一个空间坐标位置，根据该坐标位置点与各组中心值坐标位置点间的距离(即欧式距离)最小原则便可对待测样本的类别归属进行判别预测。以编号为1的样本为例，先利用3个判别函数计算出的函数值分别为0.85、-1.88、0.07，然后计算空间坐标点(0.85,-1.88,0.07)与各类中心值之间的欧式距离分别为2.89、0.99、4.90、3.92，由于与第Ⅱ中心值间的欧式距离最短，因此将该样本的突出类别判别为Ⅱ类。依此类推，可对其它样本的类别归属进行判别预测，判别结果见表5。结果表明：10个突出实例的判别结果与实际情况完全一致，判别正确率达100%。因此，在实际应用中，可根据所建立的Fisher-逐步判别分析模型对煤与瓦斯突出进行有效地预测。

Fisher-逐步判别分析模型用于煤与瓦斯突出预测，是建立在对已有煤与瓦斯类型特征规律训练学习的基础上，训练学习样本的代表性及数量对煤与瓦斯突出的准确判别预测极其重要。因此，利用该判别模型进行煤与瓦斯突出预测时需注意以下问题：①在对学习样本进行筛选时应优先考虑常用的突出预测敏感指标；②所建立的判别模型适用于煤层地质条件和采煤技术工艺类似的待预测区域，在实际工程应用过程中，可根据现场工程地质情况，尽可能选取具有代表性的实例和判别能力显著的指标；③在不增加计算负担的前提下，应尽可能增加样本数量以提高判别模型的准确性。

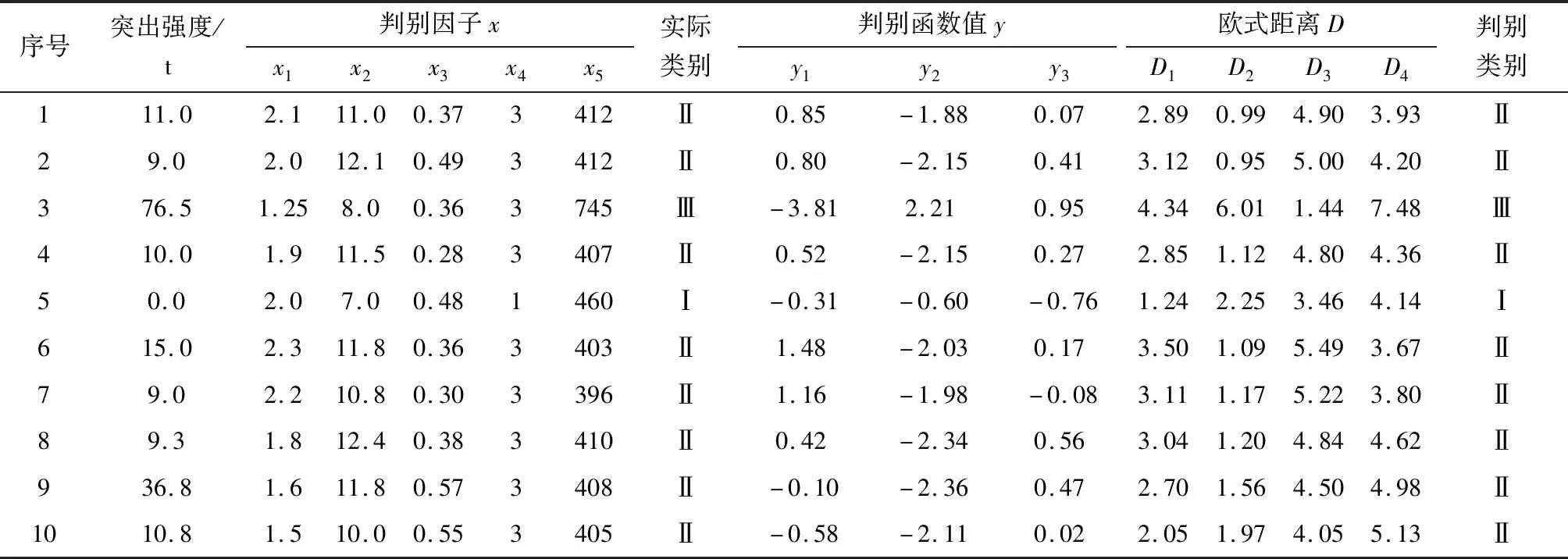
表5 待判样本数据及判别分类结果Table 5 Sample data to be determined and classification results

4 结 论

1) 为减弱非敏感指标对煤与瓦斯突出预测结果的干扰，利用逐步判别法对影响突出的5项评价指标进行筛选，选取对突出判别能力影响显著的瓦斯压力、瓦斯放散初速度和埋藏深度3个敏感指标作为判别因子。通过筛选，最大限度地避免了非显著性指标的加入而影响计算精度和判别结果，同时，也削弱了评价不同指标对煤与瓦斯突出影响程度的随意性和主观性，一定程度上反映了各指标对突出影响的差异性。

2) 基于多元统计分析理论，建立了煤与瓦斯突出预测的Fisher-逐步判别分析模型。利用所构建的判别模型对20组煤与瓦斯突出实例数据进行训练学习得出相应的判别函数，用回代估计的方法进行逐一验证，误判率仅为5%。将建立的判别模型对10组突出实例进行判别预测，判别结果与实际情况完全吻合，正确率为100%，Fisher-逐步判别分析模型是一种有效的煤与瓦斯突出预测方法。

3) Fisher-逐步判别分析模型用于煤与瓦斯突出预测，是建立在对已有煤与瓦斯类型特征规律训练学习的基础上，有一定的适用范围，在实际应用过程中需综合考虑待预测区域的煤层地质条件及开采技术工艺等。