堆叠自编码器在锚杆锚固缺陷类型识别中的应用
2020-07-13王明明孙晓云
王明明,王 莎,邢 卉,孙晓云,路 霖
(石家庄铁道大学电气与电子工程学院,河北 石家庄 050043)
锚杆锚固质量检测一直是锚杆支护施工环节的重要组成部分。锚杆锚固质量无损检测技术克服了传统检测方法耗时多且具有破坏性的不足,可以实现快速大批次的质量检测,受到学者们的广泛关注[1-3],从20世纪80年代的超声波无损检测技术发展到了现在的基于电磁超声和人工智能等技术的新型无损检测技术[4-7]。
在基于人工智能等算法的无损检测中,锚杆锚固缺陷的识别率易受提取特征的影响。目前,常用的特征提取方法包括EMD、小波分解、能量特征和时频域特征等。这些特征提取方法往往依赖于人工经验,制约了识别率的提高。2006年,Hintion利用贪心算法对自编码器网络(auto-encoder,AE)的隐含层进行优化,提出了堆叠自编码器网络(stacking auto-encoder,SAE)[8]。近年来,SAE网络在高维数据特征提取及分类识别中取得了较多成果[9-11]。本文利用SAE网络对锚杆锚固系统的缺陷特征进行提取,采用自适应时刻估计方法(Adam优化算法)对重构误差进行优化,提出一种自动确定SAE网络深度和参数的自动选层堆叠自编码器特征提取算法。通过数值模拟和物理模拟两种方法对锚杆锚固缺陷特征进行提取,并使用Softmax多分类器对锚固缺陷进行识别。本文所提算法能有效降低人工选取参数对缺陷识别精度的影响,提高了Softmax多分类器的缺陷识别率。
1 基于自动选层SAE的锚杆锚固缺陷识别算法
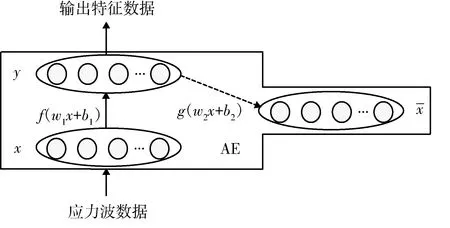
图1 AE网络模型Fig.1 AE network model
图1中的w1、b1为编码器参数,w1为n×m矩阵,b1为1×m矩阵,n为输入数据维度,m为输出特征维度;w2、b2为解码器参数,w2为m×n矩阵,b2为1×n矩阵。激活函数f、g为sigmoid函数。该网络的重构误差见式(1)。
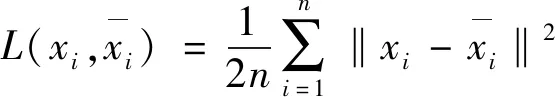
(1)
基于自动选层SAE的锚杆锚固缺陷识别算法步骤如下所述。
1) 输入数据处理:将锚杆自由端的激励响应进行归一化,作为自动选层SAE网络的输入。
2) AE参数初始化:SAE网络的训练过程是一个迭代过程,权值和阈值的初始化对最终络结果前很大影响,过大或过小的参数初始值对网络都有不好的收敛结果;所以AE网络的权值通常先随机给一个很小的值,一段取均值为0,方差为1的随机正太分布,阈值的初始值为0。
3) 参数优化:训练AE网络,使式(1)最小化,进而使AE的网络参数达到最优。
4) 自动选层网络:在满足分类准确率的前提下设定重构误差目标值,判断AE最优参数下的重构误差是否小于设定目标值;若不小于,则保存训练好的网络参数,继续增加一层AE网络,返回步骤2,直到达到误差目标设定值,跳出自动选层网络以确定SAE网络深度及参数。
5) 网络级联及分类:将训练好的AE编码器部分级联形成SAE网络,并将每层AE训练好的编码器参数作为SAE神经网络初值进行对输入数据的特征提取;利用Softmax多分类器对训练好的SAE网络输出特征进行分类训练,并对SAE网络参数进行有监督的微调,以实现锚杆锚固系统缺陷的识别。
2 基于数值模拟的锚杆锚固缺陷识别
2.1 数值模型
利用ANSYS有限元仿真软件建立了3种不同锚杆锚固缺陷的数值模型,模型结构如图2所示。
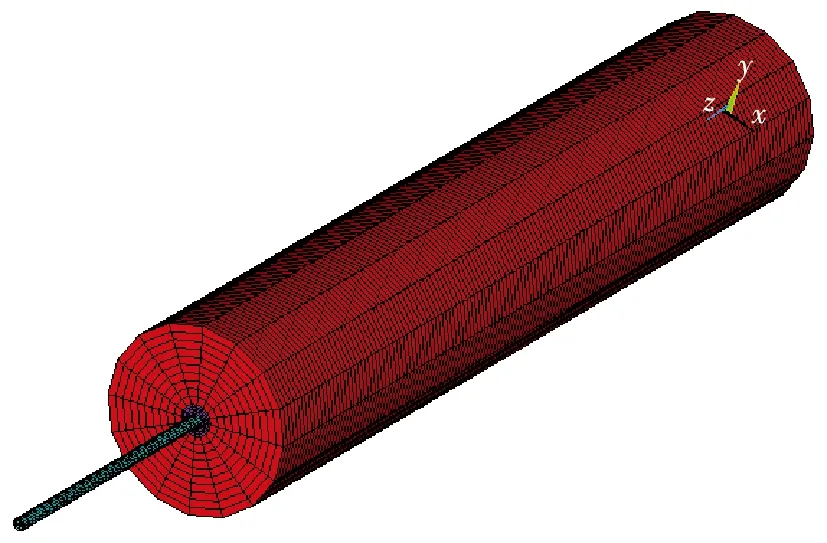
图2 ANSYS锚杆锚固系统模型Fig.2 ANSYS anchor system model
3种模型锚杆锚固模型结构为锚固前端缺陷、锚固中端缺陷以及锚固后端缺陷。通过改变每类锚杆锚固模型的结构得到90组不同锚固缺陷模型,锚杆锚固模型的几何参数见表1。钢筋、灌浆、围岩等三种材料的力学参数见表2。
2.2 数值模拟缺陷识别结果分析
在锚杆顶端截面施加5周期正弦调制波,施加力的频率为f=20~30 kHz,△f=1 kHz,采集900组每组120个样本点作为网络输入。
AE隐含层节点个数是输入节点个数的一半(向上取整),重构误差的设定值为0.001(保证缺陷识别率在95%以上)。重构误差输出如图3所示。

表1 3种锚杆锚固的几何参数Table 1 Three types of anchoring geometric parameters
注:La为自由端锚杆长度(锚杆前端面到锚固前端面);Lb为锚固部分的长度;Lc为锚固前端面到缺陷前端面的长度;Ld为缺陷的长度;h为锚固厚度

表2 三种材料的力学参数Table 2 Mechanical parameters of three materials
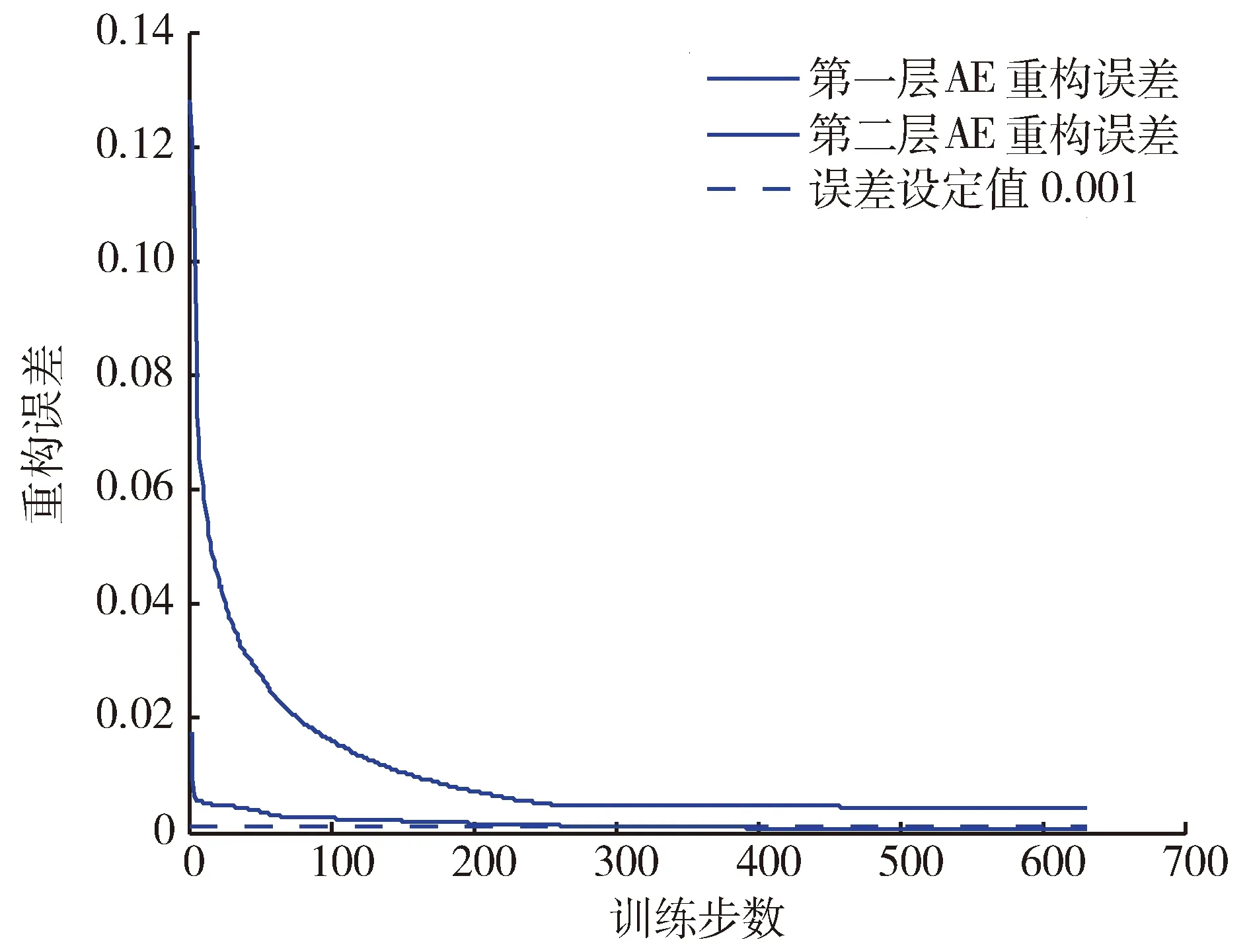
图3 仿真数据重构误差Fig.3 Simulation data reconstruction error
由图3可以看出,第一层AE和第二层AE的输出重构误差都呈下降趋势并达到收敛,第一层AE的重构误差收敛在0.004附近,未达到设定值的要求;第二层AE的重构误差达到设定值跳出自动选层网络,最后将训练好的两个AE的编码部分级联形成SAE网络,并将当前参数作为SAE每层初始参数。3种模型即锚固前端缺陷、锚固中端缺陷、锚固后端缺陷分别编码为001、010、100。归一化后数据经过SAE网络提取特征后,每类随机抽取60组共180组作为测试集,将剩下的720组作为训练集训练Softmax网络。最终缺陷识别结果如图4所示。
由图4可以看出,Softmax网络的分类结果有两个样本识别错误,识别的准确率为0.988。为了便于分析和比较,增加网络深度至5,并计算该网络深度下的重构误差、分类准确率见表3。
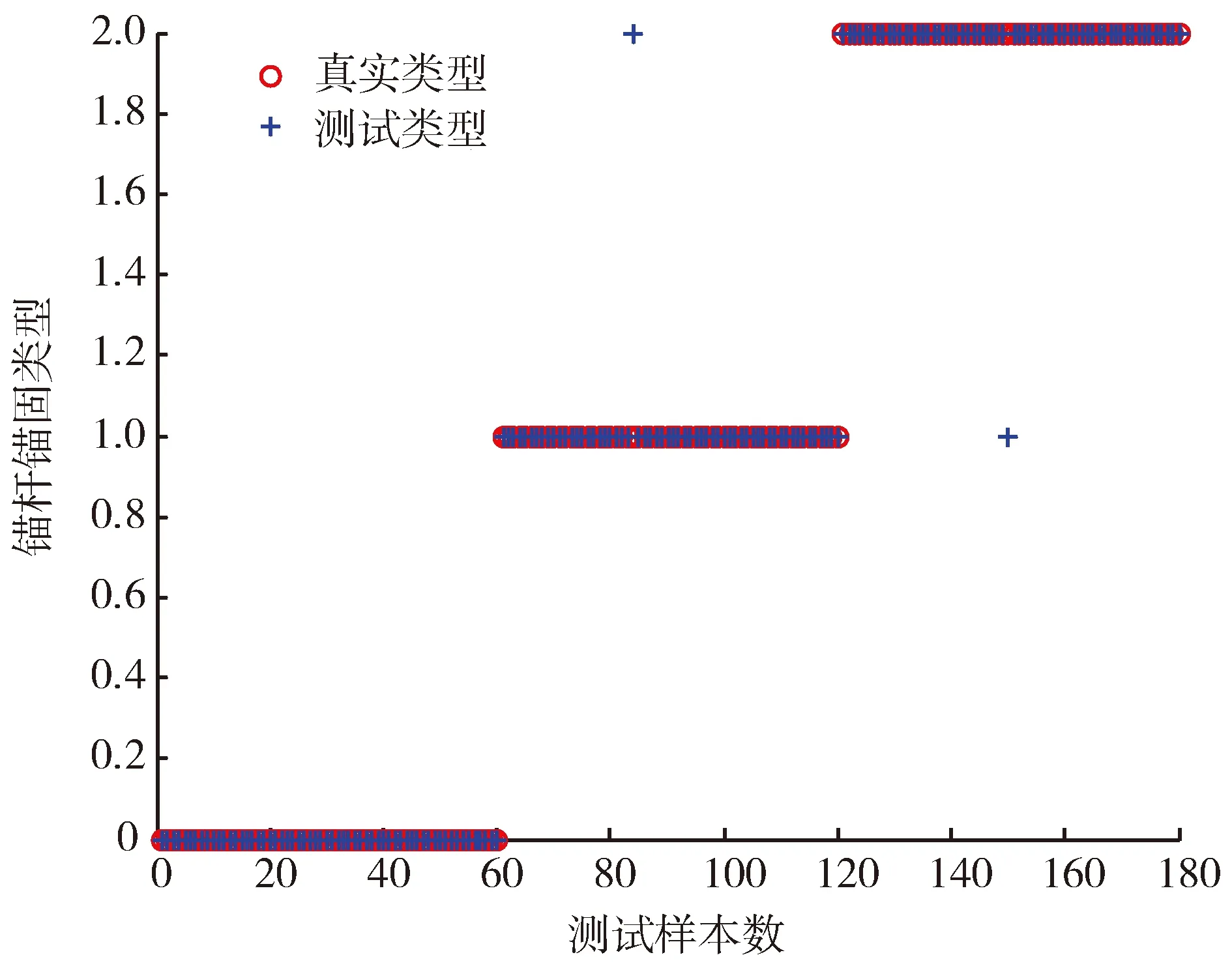
图4 仿真数据分类结果Fig.4 Simulation data classification results

表3 基于仿真数据下的不同深度的SAE网络训练数据Table 3 SAE network training data of different depths based on simulation data
由表3可以看出,网络的重构误差随网络深度的增加而下降,但分类的准确率却没有随网络深度的增加而提高,网络深度为2时准确率最高为98.8%,网络深度为5时降低至93.3%,这可能是由于网络层数的增加会使Softmax反向微调误差累加过大进而导致分类准确率的下降。为进一步验证本文算法在锚固缺陷识别方面的有效性,将本文算法与小波分解结合随机森林(RF)、主成分分析(PCA)结合SVM分别进行缺陷识别,进行10次对比的结果如图5所示。

图5 不同算法准确率Fig.5 Accuracy of different algorithms
由图5可以看出,本文算法的最低识别精度96.1%,最高识别精度98.8%,平均识别精度为97.7%。PCA结合SVM网络的最低识别精度97.2%,最高识别精度95%,平均识别精度为95.6%。小波分解结合RF网络的最低识别精度92.2%,最高识别精度95.5%,平均识别精度为93.8%。从分类结果可知,本文提出的算法识别率高于另外两种算法。
3 基于物理模拟的锚杆锚固缺陷识别
为验证算法实际应用价值,进行了物理模拟试验,如图6所示。试验锚杆样本总长度为2 m,锚固部分长度为1.5 m。其中由砂、42.5C复合硅酸盐水泥、水按比例4∶2∶1混合而成形成灌浆材料;砂、50C合硅酸盐水泥、石子(大)、石子(小)、水按比例4.2∶3.3∶3.8∶2.5∶1混合而成形成围岩材料, 缺陷为泡沫缺陷。 锚固的外壳是由直径0.3 m的PVC管包裹,锚杆锚固实物模型如7所示。螺纹钢直径为0.02 m,灌浆直径0.05 m,围岩层直径为0.3 m。
利用东华测振公司的DHDAS动态信号测试分析系统作为激励和响应信号的采集装置。采样频率为10 kHz,每个物理模型采集80组数据,每组数据包括120个样本点。
3.1 物理模型参数
试验部分使用了7类物理模型包括锚固完整、前端缺陷、中端缺陷、后端缺陷、前中缺陷、中后缺陷、前后缺陷,结构见表4。

图6 物理模拟试验Fig.6 Physical simulation test

表4 锚杆锚固模型结构Table 4 Anchor anchor model structure
3.2 物理模拟缺陷识别结果分析
表4中的7类锚杆锚固系统模型网络输出依次编码为1000000、0100000、0010000、0001000、0000100、0000010、0000001。AE隐含层节点个数是输入节点个数的一半(向上取整),重构误差的设定值为0.002(保证缺陷识别率在95%以上)。经训练,自动选层SAE网络的重构误差在第三层AE堆叠之后达到重构误差的目标设定值,从而跳出自动选层,确定了SAE网络深度。输入数据经过SAE网络进行特征提取后后,将每类锚杆的特征数据进行随机排序,每类抽取10组共70组作为测试集,将剩下的490组作为训练集。进入Softmax多分类网络中进行不同缺陷类型的锚杆锚固系统识别,锚杆锚固缺陷识别效果如图7所示。
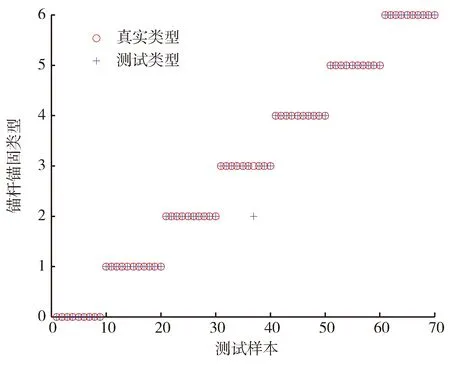
图7 自动选层SAE结合Softmax分类效果Fig.7 Automatic layer selection SAE combined with softmax classification effect
从图7中能够看出,本文方法只有1组样本识别错误,识别精度为0.985。同样对不同网络深度下的重构误差、分类准确率进行比较,见表5。
从表5可以得出,随着网络深度的增加,在重构误差方面与数值模拟结论一致,在识别准确率方面呈现先升高后下降的趋势,其中深度为3时网络的识别准确率达到最高,而自动选层网络也是选择的3层AE堆叠,说明通过自动选层网络能够得到最适宜锚杆锚固缺陷识别的网络深度。将本文算法与小波分解结合RF、PCA结合SVM分别进行10次测试的锚杆锚固质量分类,10次测试平均准确率见表6。由表6可以看出,针对实验采集的数据的分类结果,本文算法的10次平均测试准确率仍然高于后两种算法的平均准确率,也说明了该算法在在锚杆锚固缺陷识别的适用性。
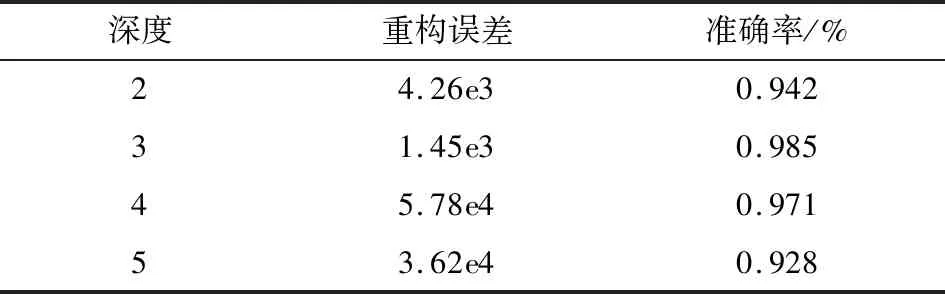
表5 基于试验数据下的不同深度的SAE网络训练数据Table 5 SAE network training data of different depths based on test data

表6 三种算法10次测试的平均准确率Table 6 Average accuracy of 10 tests for three algorithms
4 结 论
1) 利用重构误差实现对SAE网络的自动选层,能够使网络在保证缺陷识别准确率的前提下,自组织的训练网络选择深度,解决了SAE网络在分类识别中深度选择的问题。
2) 通过数值模拟模型与物理模拟模型作为网络验证的数据来源,通过与小波分解结合RF、PCA结合SVM分别进行缺陷识别对比,验证了自动选层SAE及Softmax的锚杆锚固质量分类识别算法在锚杆锚固缺陷识别方面具有很好的性能。
