SWMM模型参数敏感度分析应用研究

郭旖琪 马立山 王利民 杨国丽 张海平

(河北建筑工程学院，河北 张家口 075000)

0 引 言

城市化虽然加速了城市的发展，但也使内涝问题频频发生.住建部在2010年的调查中发现，近两年来在351个大小城市中，有60%以上的城市都出现了内涝问题[1].城市雨洪模型作为研究城市内涝的重要工具现应用较为广泛，但由于模型中参数很多，盲目的调参既费时，又达不到预期效果[2].根据SWMM(Storm Water Management Model)手册给定范围选取经验值模拟，计算结果与实际结果往往相差很大，为提高模型模拟的精度，应对研究区模型选参时进行简捷科学的敏感度分析和参数率定来确定参数合理数值.

黄金良等人[3]基于Morris法对SWMM模型中相关参数敏感度分析，对模型不确定性和参数进行分析识别.Sun等人[4]运用GLUE法对SWMM模型进行了不确定分析和参数取值的确定.Liong等人基于遗传算法(Genetic Algorithm,GA)在SWMM模型中6 km2区域内利用六次降雨数据校核验证模型.刘苏宁等人[5]利用PSO对模型参数进行率定，取得很好效果.但从上述可以看出在应用优化算法对参数率定时，约束条件都较为单一，计算结果反应出的情况不够全面.

本研究利用扰动分析法对模型参数进行局部敏感度分析确定出参数项对计算结果影响程度，选取拉丁超立方抽样方法建立学习样本，将总产流和峰值流量同时作为率定目标建立多目标粒子群优化算法进行模型参数率定.

1 模型参数

1.1 研究区SWMM模型建立

本文选取L市的某一城区作为研究区，总面积为1261.59 hm2，研究区内土地利用情况大致可以分为建筑屋面、道路及绿地，其中绿地占比为31.6%.为了提高模型模拟的精确度应对收集的各项数据进行整理.

管网数据是在L市保证基本排水能力的基础上，根据排水分区进行管线梳理和概化，得到最终管网概化后的信息如下表1，汇水区域概化是根据地形图和主要道路划分出较大的集水区，接着利用泰森多边形方法，根据节点的分布对集水区进行细划，划分成多个子汇水区，最后结合管网走向、街道分布和建筑物等情况人工稍作调整，最终得到子汇水区43个，概化后的研究区域在SWMM模型中建立，如下图1.

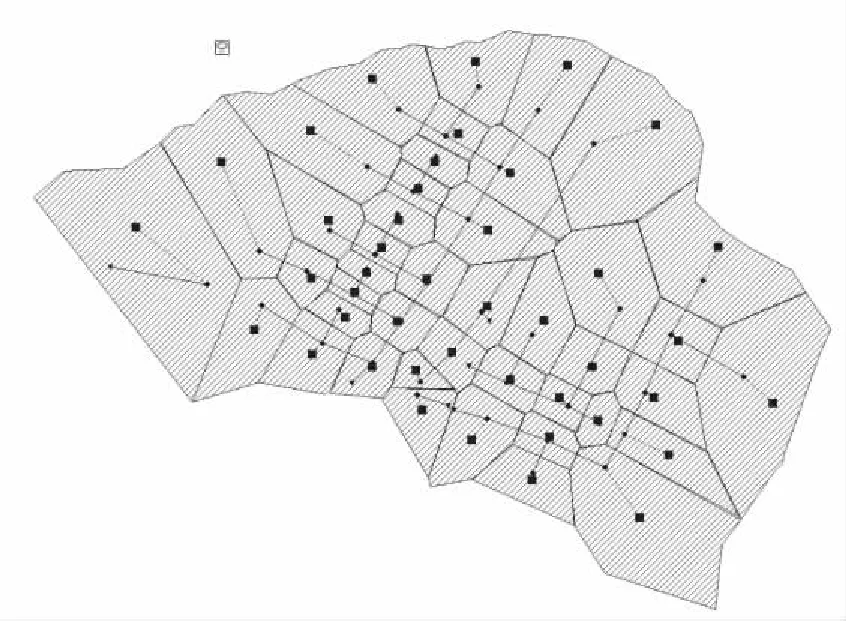
图1 SWMM模型概化后研究区

表1 管网概化信息

选取降雨事件时通常是以实测的降雨数据作为建立模型时降雨的输入数据[6]，本文采用一场24 h的实测降雨数据rain1作为降雨事件的输入值用于模型的率定.

1.2 参数选取

本研究采用Horton与非线性水库模型来模拟降雨径流过程.建立模型时需要输入的参数项及它们的取值范围如表2.模型的参数分为真实参数和经验参数，真实参数可根据原始收集的数据和地理信息系统分析工具来确定，经验参数则是根据各子汇水区下垫面情况及土地利用等信息在SWMM手册中凭经验取得.

表2 参数项信息

利用SWMM模型模拟时，一些经验参数对计算结果影响很大，这时应对经验参数进行率定，进而可以更好的反映实际降雨情况.结合现有资料数据，本研究对N-Imperv、N-Perv、S-Imperv、S-Perv、MaxRate、MinRate、Manning-N这七项参数进行分析，以使模型计算值尽可能与实测值接近.

2 模型参数敏感度分析

2.1 敏感度分析

在模型建立中对模型进行敏感度分析是必须的，它可以确定参数对计算结果的影响，筛选出一些对结果影响大的重要参数，避免模型在参数率定过程中的盲目性同时能提高率定效率[7].敏感度分析可分为局部敏感度分析和全局敏感度分析两种，常见的敏感度分析法一般有：Morris法、逐步回归法、偏秩相关法、Sobol法等，扰动分析法是目前应用最为广泛的一种局部敏感度分析方法[8].

2.2 扰动分析法原理

扰动分析法是将待分析参数选出其中一个参数项，在基准值基础上按固定扰动步长来改变其取值，并采取“控制变量”的方法，使其余各参数值不变，计算出参数在固定步长波动时对模型计算结果的影响.其中基准值是根据SWMM手册范围和收集到的数据信息经验取得的数值，每次扰动对计算结果变化率的表达式为(其中i为待分析参数项编号，即i=1,2,…,n)：

(1)

式中:αi——参数i扰动后变化率

Ti扰动、Ti基准——参数i扰动变化后计算值、参数i基准值时计算值

本文将参数的扰动步长确定为10%，参数的取值分别为基准值的80%、90%、100%、110%、120%，计算结果为总产流和峰值流量，各项参数计算值的变化率可由式(1)求得.

3 模型参数率定

3.1 拉丁超立方抽样原理

在优化算法构建中，必须有相对应的学习样本用来进行程序的训练.由于收集到的现有数据有限，所以应采取科学的抽样方法建立学习样本.本研究采用拉丁超立方抽样，拉丁超立方抽样的样本点分布较均匀，避免了样本点的重复性，各样本点之间相互具有独立性[9]，这就可使在维度不大的情况下，样本点同样也可以达到很好的抽样效果.拉丁超立方抽样是指将每个变量在给定范围内等区间的分层，并在每层随机抽取一个样本值，将各个变量所得的值随机组合，得到样本数据.

本研究中，学习样本设定为100组，根据SWMM手册和收集到的资料，可知五项参数的取值范围，将每项参数在取值范围内分成100个等区间，在每个区间随机抽取一个值，再将得到的五项100组数值随机组合(部分)如表3.将100组参数项输入SWMM模型中得到100组计算值，选出对模型模拟有重要意义的计算参数项，峰值流量和总产流共两项，将100*(5+2)组数据作为学习样本进行接下来程序训练.

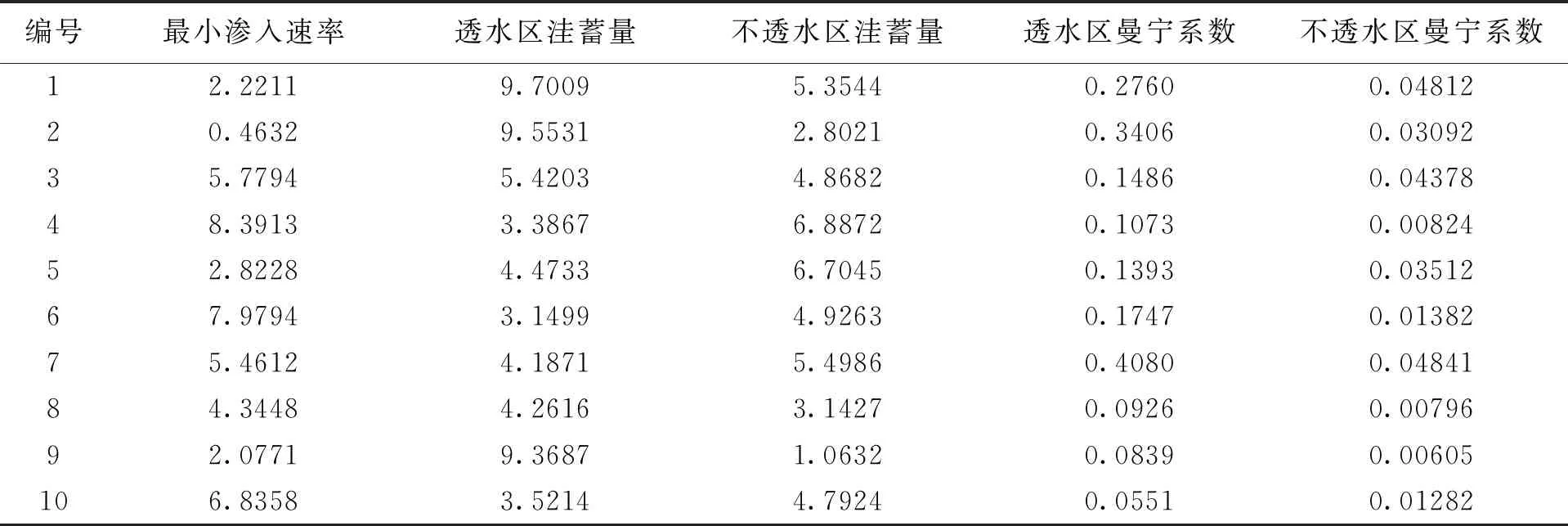
表3 五项数值组合(其中10组)

3.2 粒子群特点

对输入数据中的经验参数科学优化，可以使计算结果更接近真实情况.常见的优化算法种类很多，如遗传算法、模拟退火、神经网络等.Kennedy博士和Eberhart[10]博士于1995年提出了一种通过模拟鸟群捕食行为来设计的群智能优化算法，即粒子群算法(Particle Swarm Optimization，简称PSO)[11].粒子群算法相对于其它算法来说，计算简单，容易实现，无需梯度信息，参数少，而且收敛速度较快[12].在水文模型参数优化算法中，粒子群优化算法是现阶段使用的高效方法.

3.3 粒子群

粒子群算法中每个寻优问题的解都被想像成对应于搜索空间中一只鸟的最佳位置，其称为“粒子”.每个粒子都有自己的初始速度和位置(决定距离和方向)，所有粒子都在一个D维(求解值的数量)空间进行搜索.粒子是由一个目标函数计算出适应值，进而找到个体极值和全局最优解以判断目前的位置情况，并不断更新粒子的位置和速度.每一个粒子能记住所搜寻到的最佳位置，以此为依据来寻找下一个解[13].

本研究在粒子群算法优化中为了使计算结果的峰值流量和总产流均模拟精确度较高，同时将峰值流量和总产流作为率定目标，成为多目标优化问题进行优化计算.因此，优化率定的目标函数为如下形式[14]：

F=min[(Qp)s-(Qp)r]2+[(Qt)s-(Qt)r]2

(2)

式中:Qp、Qt——分别为峰值流量和总产流

s、r——分别为模拟计算值和实际测量值

初始化粒子群的群体规模设置为n=20，算法迭代300次作为此次优化算法的终止条件，加速常数为c1=c2=2.

4 研究结果

4.1 敏感度分析结果

根据已求得各参数变化率结果，可绘制扰动变化率拟合曲线图，如图2，横坐标为扰动系数，纵坐标为各参数项波动后对计算值的变化率.

图2 峰值流量(A)和总产流(B)的扰动变化率拟合曲线

扰动变化率拟合曲线图中斜率代表参数对计算结果影响的情况，斜率绝对值越大表示参数对计算值的敏感度越高.分析结果表明，参数对峰值流量而言，不透水区曼宁系数和透水区曼宁系数为敏感参数，最大渗入速率和管道曼宁系数为不敏感参数；参数对总产流而言，不透水区曼宁系数、最小渗入速率和透水区曼宁系数为敏感参数，最大渗入速率和管道曼宁系数为不敏感参数.根据上述分析，最大渗入速率和管道曼宁系数为计算结果不敏感参数，可以在参数值选取时设置为经验值，在下一步率定优化时只考虑剩余五个参数项，这样既可以节省时间也可以提高效率.

4.2 粒子群优化结果及检验

算法运行后可发现，随着迭代次数的增多，目标函数值(即适应度值)不断地趋近于零，在迭代150次后趋于稳定状态，得到参数的最优组合如表4.

表4 优化参数组合

将率定后的参数组合再次输入模型中，得到优化后峰值流量相对误差在6.67%，总产流相对误差在4.27%，相对误差较小，精确度较高.

为验证优化后参数组合的合理性，利用优化后模型对当地一场实测降雨数据rain2进行模拟，得到峰值流量相对误差16.34%，总产流相对误差在5.74%，模型计算结果与实际情况较吻合，说明率定方法适用于研究区模型的参数率定.

5 结 论

在本研究区建立的雨洪模型利用局部敏感度分析中的扰动分析法对七项参数进行计算分析.结果表明参数对峰值流量而言，不透水区曼宁系数和透水区曼宁系数为敏感参数；参数对总产流而言，不透水区曼宁系数、最小渗入速率和透水区曼宁系数为敏感参数.由于最小渗入速率与下渗量息息相关，最小渗入速率增加，下渗量增加，导致计算结果中的总产流减少，不透水区曼宁系数和透水区曼宁系数这两项输入参数对研究区降雨的滞蓄量和排出状态关系密切，从而会影响着峰值流量和总产流的变化.

利用峰值流量和总产流两项计算结果同时作为率定目标，建立多目标粒子群优化算法，利用两组降雨数据对模型参数进行率定及验证，结果表明方法适用于研究区模型参数率定.科学优化后的模型可对城市雨洪风险问题提供一些前瞻性的建议.